Steady-State Fluid Flow with a Free Surface

Note

The project file for this example is available to be viewed/run in FLAC3D or FLAC2D.[1] The project’s main data files are shown at the end of this example. 2D equivalents can be found in the FLAC2D example directory.

This example is the classical problem of steady-state seepage flow through a homogeneous embankment with vertical slopes exposed to different water levels and resting on an impermeable base. The total discharge, \(Q\), and the length of seepage face, \(s\), are compared to the exact solutions. Figure 1 shows the geometry and boundary conditions of the problem.

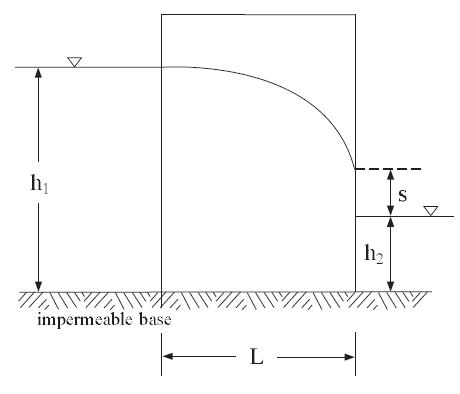
../../../../../_images/freesurface-flow-boundary.png — Figure 1: Problem geometry and boundary conditions.

The fluid is homogeneous, flow is governed by Darcy’s law, and it is assumed that the pores of the soil beneath the phreatic surface are completely filled with water and the pores above it are completely filled with air. The width of the dam is \(L\), the head and tail water elevations above the impervious base are \(h_{1}\) and \(h_{2}\), respectively.

The exact solution for the total discharge through a dam section of unit thickness was shown by Charny (Harr 1991) to be given by Dupuit’s formula:

(1)\[Q\ =\ k\ \rho_w\ g\ \cdot\ {h^2_1 - h^2_2 \over {2L}}\]

where \(k\) is mobility coefficient, \(\rho _{w}\) is water density and \(g\) is gravity. The length, \(s\), of the seepage face (elevation of the free surface on the downstream face of the dam above \(h_{2}\)) was obtained by Polubarinova-Kochina (1962), and is given in Figure 2 as a function of the characteristic dimensions of the problem.

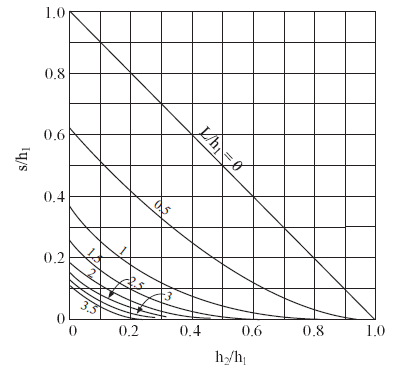
../../../../../_images/freesurface-flow-analytical-solution.png — Figure 2: Seepage face solution after Polubarinova-Kochina (1962).

The FLAC3D simulation is conducted for a particular set of parameters:

L	=	9 m
h₁	=	6 m
h₂	=	1.2 m

Several material properties are used:

permeability (\(k\))	10^-10 (m/sec)(Pa/m)
porosity (\(n\))	0.3
water density (\(\rho_w\))	1000 kg/m³
water bulk modulus (\(K_f\))	1000 Pa
soil dry density (\(\rho\))	2000 kg/m³
gravity (\(g\))	10 m/sec²

Two cases corresponding to two different initial conditions have been studied:

CASE 1:	The water level in the embankment is initially at \(h\) = \(h_2\) = 1.2 m. The upstream level is raised to \(h\) = \(h_1\).

CASE 2:	The water level is initially at \(h\) = \(h_1\) = 6 m. The downstream level is lowered to \(h\) = \(h_2\).

The data file for Case 1 is listed in “FreeSurfaceSteadyStateFluidFlow-Case1.dat”, and in “FreeSurfaceSteadyStateFluidFlow-Case2.dat” for Case 2. The grid and boundary conditions are the same for both cases. The grid contains 30 zones in width, 20 zones in height, and 1 zone in thickness. The boundary conditions correspond to a static pore-pressure distribution up to level \(h_{1}\) on the upstream face, and up to \(h_{2}\) on the downstream face, zero pore pressure from level \(h_{2}\) to \(h_{1}\) on the downstream face, and to no-flow conditions across the remaining boundaries. The differences between the two cases are the initial pore pressure and saturation distributions. In Case 1, saturation and pore pressure are zero above \(h_2\). Below that level, the saturation is 1 and the pressure is hydrostatic. In Case 2, saturation is 1 for all gridpoints, and the pore pressure inside the mesh follows a gravitational gradient. The numerical simulation is carried out until steady-state conditions are detected.

To speed the calculation to steady state, the water bulk modulus is given a small value (\(K_{f}\) = 10³ Pa) compatible with free surface stability. (The criterion used is \(K_{f}\geq 0.3\rho _{w}gL_{z}\), where \(L_{z}\) is the maximum vertical zone dimension in the vicinity of the phreatic surface, as discussed in Time Scales.)

The final flow pattern is similar for both initial conditions (see Figure 3 and Figure 4). The numerical value of seepage length is defined as the distance on the downstream face of the dam, between the tail water elevation and the point where the magnitude of the flow vector vanishes. The analytical value of seepage length is determined from Figure 2. For this particular problem, \(h_{2}/h_{1}\) = 0.2, \(L/h_{1}\) = 1.5, and the value of \(s/h_{1}\) is thus 0.1. As seen in the figures, the numerical value of seepage length compares well with the analytical solution sketched there as a bold line. A FISH function, qflac, is used to determine the discharge, \(Q\), per unit thickness of the dam: the steady-state numerical value is 1.914 × 10^-6m²/s for Case 1; and 1.912 × 10^-6m²/s for Case 2. The values are close to the analytic value of 1.920 × 10^-6m²/s, as determined from Equation (1) for this particular problem.

break

../../../../../_images/freesurface-flow-vectors-case-11.png — Figure 3: Steady-state flow vectors and seepage face solution—Case 1.

../../../../../_images/freesurface-flow-vectors-case-21.png — Figure 4: Steady-state flow vectors and seepage face solution—Case 2.

Case 1 is repeated to test fluid flow across two sub-grids that are connected by using either the zone attach command or the zone interface create command. “FreeSurfaceSteadyStateFluidFlow-Case1-Attach.dat” lists the commands for flow across an attached grid, and “FreeSurfaceSteadyStateFluidFlow-Case1-Interface.dat” lists the commands for flow across an interface. Both model results are nearly identical to the original Case 1; the values for discharge for both the Attach and Interface models are 1.924 × 10^-6m²/s and 1.913 × 10^-6m²/s, respectively. Compare Figure 5 and Figure 6 to Figure 3. Note that if maximum-edge is specified with the zone interface element command, then the interface will act as an impermeable boundary. Remove the semicolon from the line of zone.interface.1.element.maximum-edge to observe this response.

break

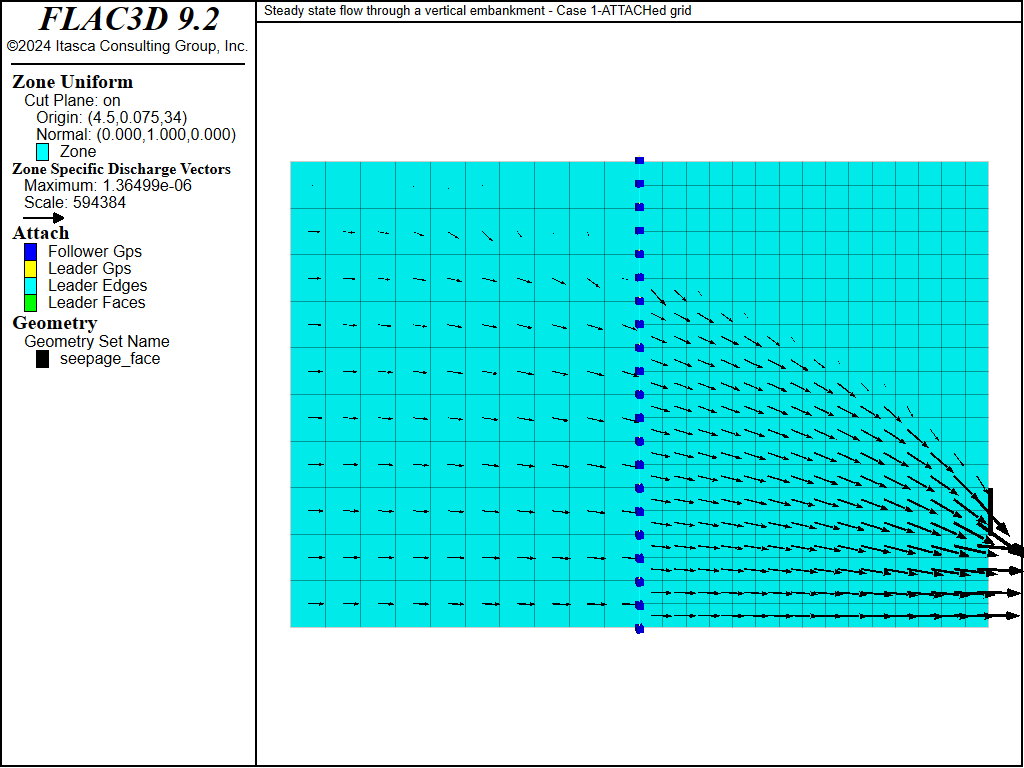
../../../../../_images/freesurface-flow-vectors-attach.png — Figure 5: Steady-state flow vectors for attached grid—Case 1.

../../../../../_images/freesurface-flow-vectors-int.png — Figure 6: Steady-state flow vectors for grid with an interface—Case 1.

Reference

Harr, M. E. Groundwater and Seepage. Dover (1991).

Data Files

FreeSurfaceSteadyStateFluidFlow-Case1.dat

model new
model title "Steady state flow through a vertical embankment - case 1"
zone create brick size 30 1 20 point 1 (9.0,0,0) point 2 (0,0.15,0) ...
                               point 3 (0,0,6.0)
zone face skin
zone face group 'BC=Outflow' range group 'East' position-z 0 1.19
; --- fluid flow model ---
model configure fluid-flow
zone fluid unsaturated cutoff 0.0
zone fluid property mobility-coefficient 1e-10 porosity 0.3 ...
                    fluid-modulus 1e3 fluid-density 1e3 
zone gridpoint initialize pore-pressure 1.2e4 gradient (0,0,-1e4) 
zone face apply pore-pressure 6.0e4 gradient 0 0 -1e4 range group 'West'
zone face apply pore-pressure 1.2e4 gradient 0 0 -1e4 range group 'Outflow'
zone face apply pore-pressure 0.0 range group 'East' group 'Outflow' not
; Add particle tracks
zone fluid track create line begin (0,0.1,0.5) end (0,0.1,5.5) ...
                             segments 12 group "set1"
zone fluid track active on
; --- settings ---
model gravity 10
model save 'case1s'

; --- explicit test ---
model solve-fluid time 4e8
model save 'case1e'

; --- implicit test ---
model restore 'case1s'
zone fluid implicit servo on 
model solve-fluid time 4e8
model save 'case1i'

FreeSurfaceSteadyStateFluidFlow-Case2.dat

model new
model title "Steady state flow through a vertical embankment - case 2"
zone create brick size 30 1 20 point 1 (9.0,0,0) point 2 (0,0.15,0) ...
                               point 3 (0,0,6.0)
zone face skin                               
zone face group 'BC=Outflow' range group 'East' position-z 0 1.19
; --- fluid flow model ---
model configure fluid-flow
zone fluid unsaturated cutoff 0.0
zone fluid property mobility-coefficient 1e-10 porosity 0.3 ...
                    fluid-modulus 1e3 fluid-density 1e3 
zone gridpoint initialize pore-pressure 6.0e4 gradient (0,0,-1e4) 
zone face apply pore-pressure 6.0e4 gradient 0 0 -1e4 range group 'West'
zone face apply pore-pressure 1.2e4 gradient 0 0 -1e4 range group 'Outflow'
zone face apply pore-pressure 0.0 range group 'East' group 'Outflow' not
; --- settings ---
model gravity 10
model save 'case2s'

; --- explicit test ---
model solve-fluid time 4e8
model save 'case2e'

; --- implicit test ---
model restore 'case2s'
zone fluid implicit servo on 
model solve-fluid time 4e8
model save 'case2i'

FreeSurfaceSteadyStateFluidFlow-Case1-Attach.dat

model new
model title ...
     "Steady state flow through a vertical embankment - Case 1-ATTACHed grid"
zone create brick size 10 1 10 point 0 (0,0,0)      point 1 (4.5,0,0) ...
                               point 2 (0,0.15,0)   point 3 (0,0,6) 
zone create brick size 15 1 20 point 0 (4.5,0,0)    point 1 (9,0,0)   ...
                               point 2 (4.5,0.15,0) point 3 (4.5,0,6) merge off
zone attach by-face
zone face skin
zone face group 'BC=Outflow' range group 'East2' position-z 0 1.19
; --- fluid flow model ---
model configure fluid-flow
zone fluid unsaturated cutoff 0
zone fluid property mobility-coefficient 1e-10 porosity 0.3 ...
                    fluid-modulus 1e3 fluid-density 1e3 
zone gridpoint initialize saturation 0.0
zone gridpoint initialize pore-pressure 1.2e4 gradient (0,0,-1e4) ...
                          range position-z 0.0 1.19
zone face apply pore-pressure 6.0e4 gradient 0 0 -1e4 range group 'West1'
zone face apply pore-pressure 1.2e4 gradient 0 0 -1e4 range group 'Outflow'
zone face apply pore-pressure 0.0 range group 'East2' group 'Outflow' not
; --- settings ---
model gravity 10

model solve-fluid time 4e8
model save 'case1-att'

FreeSurfaceSteadyStateFluidFlow-Case1-Interface.dat

model new
model title ...
      "Steady state flow through a vertical embankment - case 1 - INTERFACE"
zone create brick size 15 1 10 point 0 (0,0,0)    point 1 (4.5,0,0) ...
                               point 2 (0,0.15,0) point 3 (0,0,6) ...
                               group 'Left'
zone create brick size 15 1 20 point 0 (4.5,0,0)  point 1 (9,0,0) ...
                               point 2 (4.5,0.15,0) point 3 (4.5,0,6) ...
                               group 'Right' 
zone face skin
zone face group 'BC=Outflow' range group 'East2' position-z 0 1.19
; --- interface ---
zone interface create by-face separate range position-x 4.5 group 'Right'
; --- fluid flow model ---
model configure fluid-flow
zone fluid implicit off
zone fluid unsaturated cutoff 0
zone fluid property mobility-coefficient 1e-10 porosity 0.3 ...
                    fluid-modulus 1e3 fluid-density 1e3 
zone gridpoint initialize saturation 0.0
zone gridpoint initialize pore-pressure 1.2e4 gradient (0,0,-1e4) ...
                          range position-z 0.0 1.19
zone face apply pore-pressure 6.0e4 gradient 0 0 -1e4 range group 'West1'
zone face apply pore-pressure 1.2e4 gradient 0 0 -1e4 range group 'Outflow'
zone face apply pore-pressure 0.0 range group 'East2' group 'Outflow' not
; --- settings ---
model gravity 10
; --- test ---
model solve-fluid time 4e8
model save 'case1-int'

Endnotes

⇄

⇐ One-Dimensional Filling of a Porous Region | Spreading of a Groundwater Mound ⇒

Was this helpful? ...

Updated: Dec 19, 2024