Steady-State Convection in a Saturated Porous Medium Heated from Below

Note

To view this project in FLAC3D, use the menu command Help ‣ Examples…. The project’s main data files are shown at the end of this example.

The problem of steady-state convection in a porous layer heated from below (the Horton-Rogers-Lapwood Convection Problem) is a classical convection application. We consider a saturated layer of finite thickness and lateral extent. The temperature is fixed at the top and the base of the layer. The boundaries are impermeable to fluid flow, and the lateral boundaries are adiabatic. The problem solution depends on the value of the Rayleigh number, \(Ra\), which is defined for this problem as

(1)\[Ra = {k \over k^T} (\rho_0 c_w) \cdot (\rho_0 g H) \beta_f (T_1 - T_0)\]

where \(H\) is the height of the layer, and \(T_1\), \(T_0\) are the temperatures at bottom and top (see, for example, Lapwood 1948). For Rayleigh numbers below the minimum critical value of \(4 \pi^2\) (or about 39.48), the problem has a trivial steady-state solution, which corresponds to zero specific discharge (the conduction solution). For Rayleigh numbers above \(4 \pi^2\), non-trivial solutions may also exist in the form of convection cells. A spectrum of different steady convection modes can be realized physically; we consider various geometrical aspect ratios and Rayleigh numbers, and we seek some of these solutions in this section.

Saturated Porous Cube

The first example concerns two-dimensional convection in a cube. With the properties and dimensions adopted in the model, the Rayleigh number for this problem is approximately 42. This quantity is larger than the critical value of \(4 \pi^2\). Therefore, non-trivial solutions can be expected. We will illustrate one of these solutions: a two-dimensional roll, which we compare to an analytic solution derived from a linear stability analysis. First, we start with an illustration of the computational methodology. The data file for this example is “HRL-Convection-Cube-LowRa.dat”.

We take, as initial conditions, the conduction solution (see Equation (1) and (3) in natural convection). In FLAC3D, the transient equations are solved for the fluid, and a value for the bulk modulus of the fluid must be provided. In the present algorithm, this value affects the magnitude of stable timestep adopted for the simulation. We select a value of 2 × 10⁵ Pa, which means that, for the property values and zone size adopted in the explicit simulation, the fluid timestep is one order of magnitude smaller than the thermal timestep.

For an explicit mode of calculation, we fix the thermal timestep at 5.5 × 10¹⁰ seconds and the fluid timestep at 5.5 × 10⁹ seconds. We then design a “supersolve” command with the FISH language, which takes one thermal step and 10 fluid-flow steps for each super-step in the calculation. In this way, the thermal and fluid times are synchronized after execution of each super-step.

The explicit mode of calculation is very inefficient for this problem. Alternatively, to reduce the computation time, we use the implicit mode of calculation with a timestep ten times larger for both the thermal and fluid simulations.

The settings for the implicit calculation are

zone fluid implicit on
zone thermal implicit on
model fluid   timestep fix 5.5e10
model thermal timestep fix 5.5e11

The implicit mode commands are listed below.

The FLAC3D grid is shown in Figure 1, together with the location of monitoring points. The initial pore pressure contours and temperature contours corresponding to the conduction solution for a fluid with temperature-dependent density are plotted in Figure 2 and Figure 3.

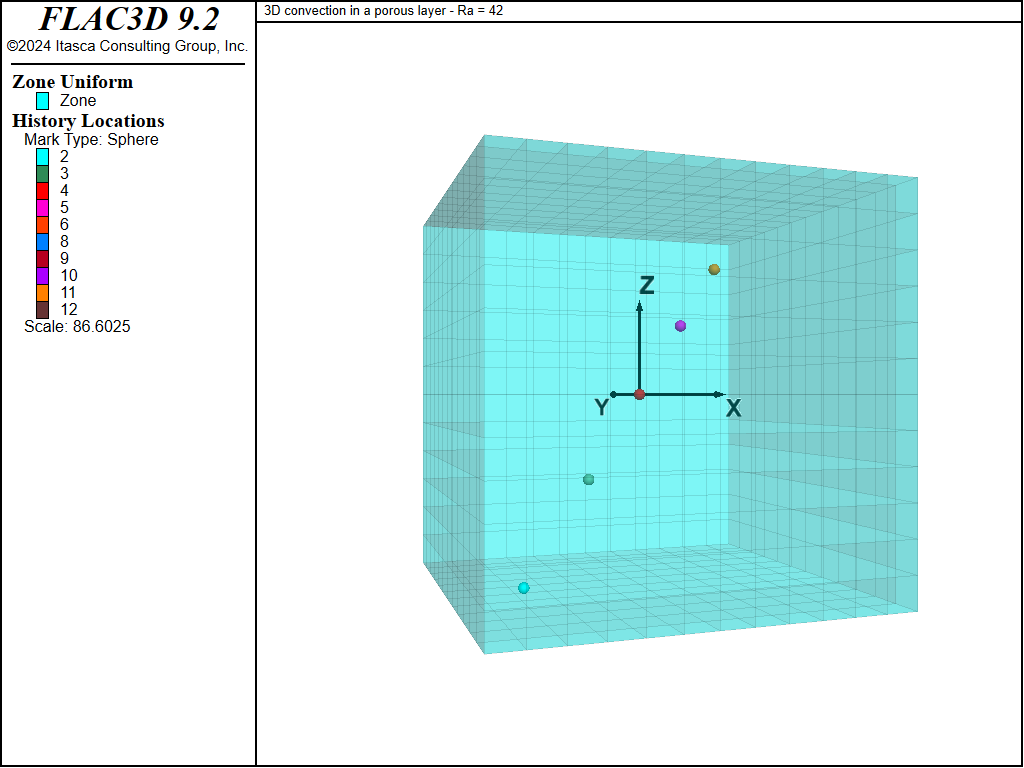
Figure 1: FLAC3D grid and location of monitoring points.

With this type of problem, there is more than one possible solution (one conduction and one or more advection solutions, depending on the Rayleigh number). The conduction solution is usually obtained, and a small perturbation is often needed to make the system bifurcate to one of the possible convection solutions (e.g., a random distribution of a property, or tilting the gravity slightly). In this example, we were able to obtain a two-dimensional roll by tilting the angle of gravity by 0.06° in the \(x\)-direction. The perturbation is applied for a finite number of steps and then removed. Note that if the same example is run for a long enough time without any perturbation, there seems to be enough numerical noise to cause the solution to bifurcate, but this time to a three-dimensional convection cell.

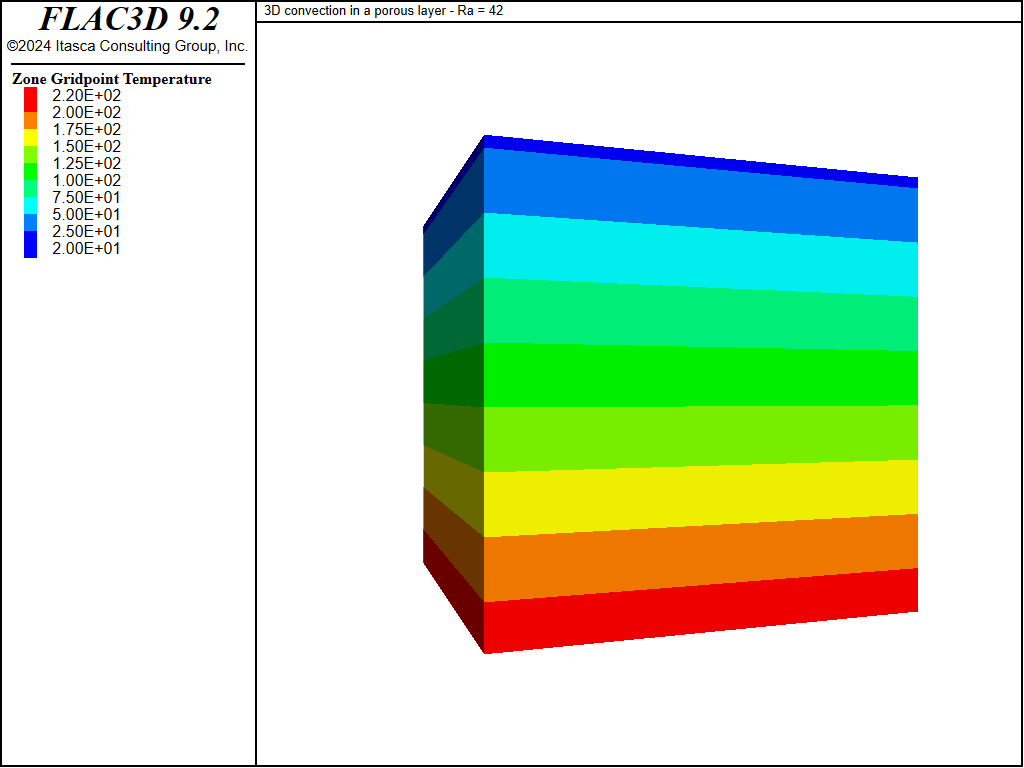
Figure 2: Initial temperature contours—conduction solution.

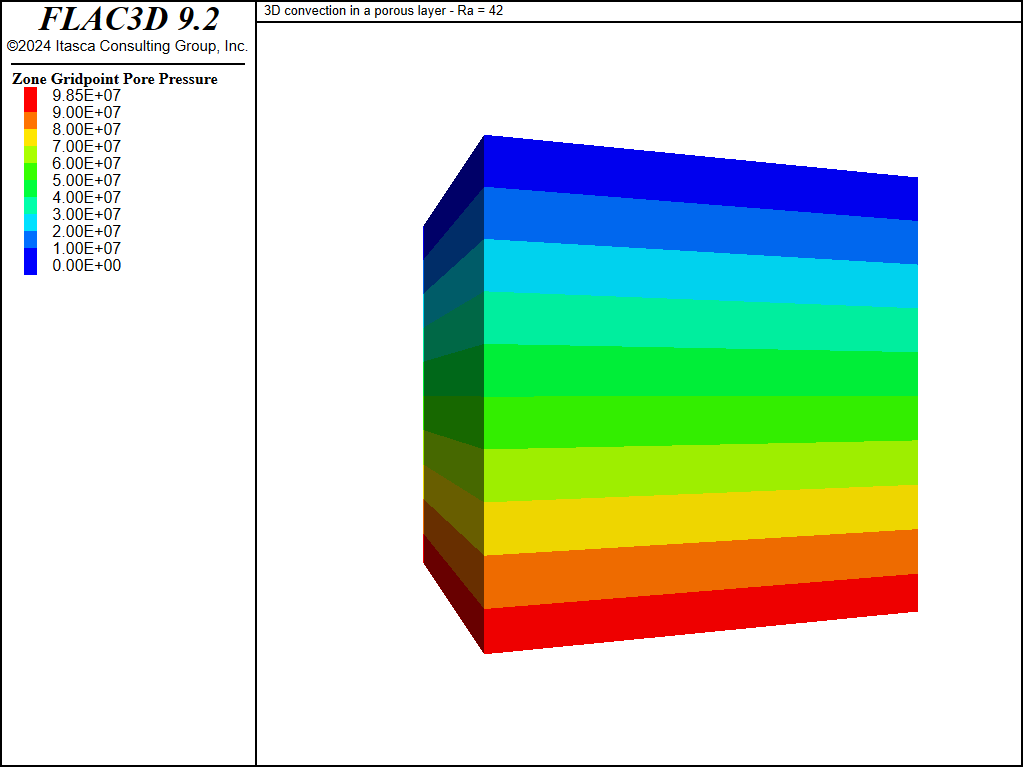
Figure 3: Initial pore pressure contours—conduction solution.

Starting with the conduction solution, we take a number of calculation super-steps. For a Rayleigh number close to critical (as in this example), the number of super-steps that needs to be taken before noticeable changes are detected can be quite large. After 100 super-steps, hardly any change is seen in the temperature in the model; however, a convection cell starts to form. This may be seen in Figure 4, where flow vectors are plotted on a background of temperature contours.

The steady-state solution has not been reached. As the simulation proceeds, the temperature begins to evolve in the model, and the convection cells develop further into a two-dimensional roll. Figure 5 and Figure 6 show the temperature contours and evolution of temperature with time at the control points after 700 super-steps.

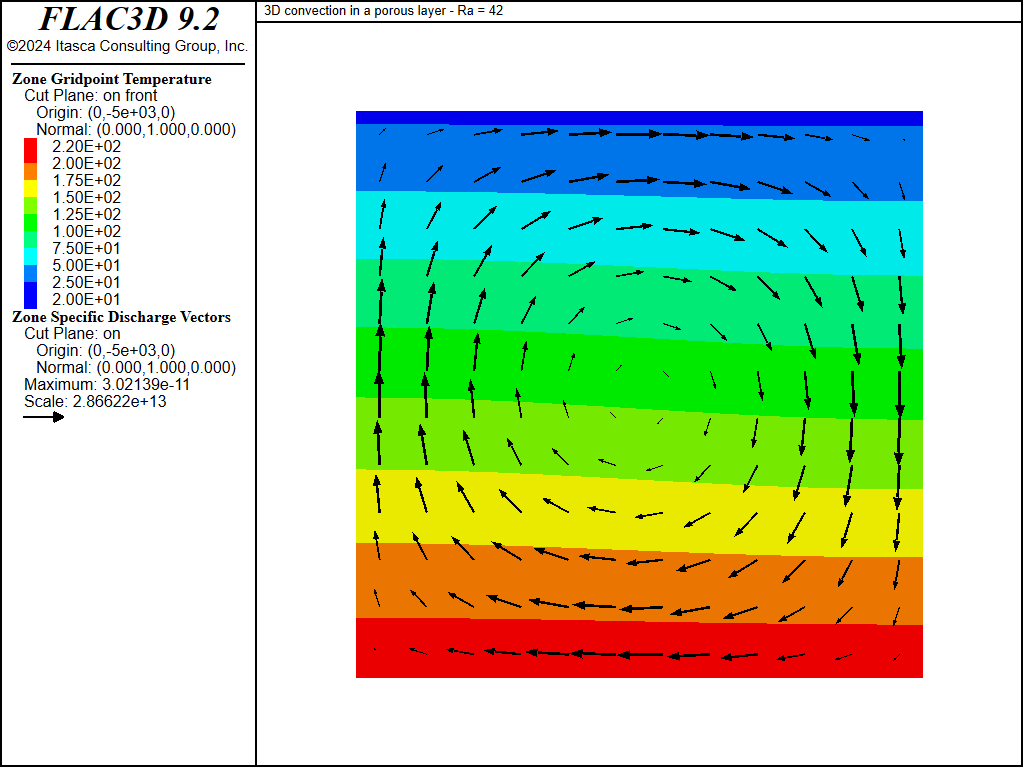
Figure 4: Temperature contours and flow vectors after 100 super-steps (Ra = 42).

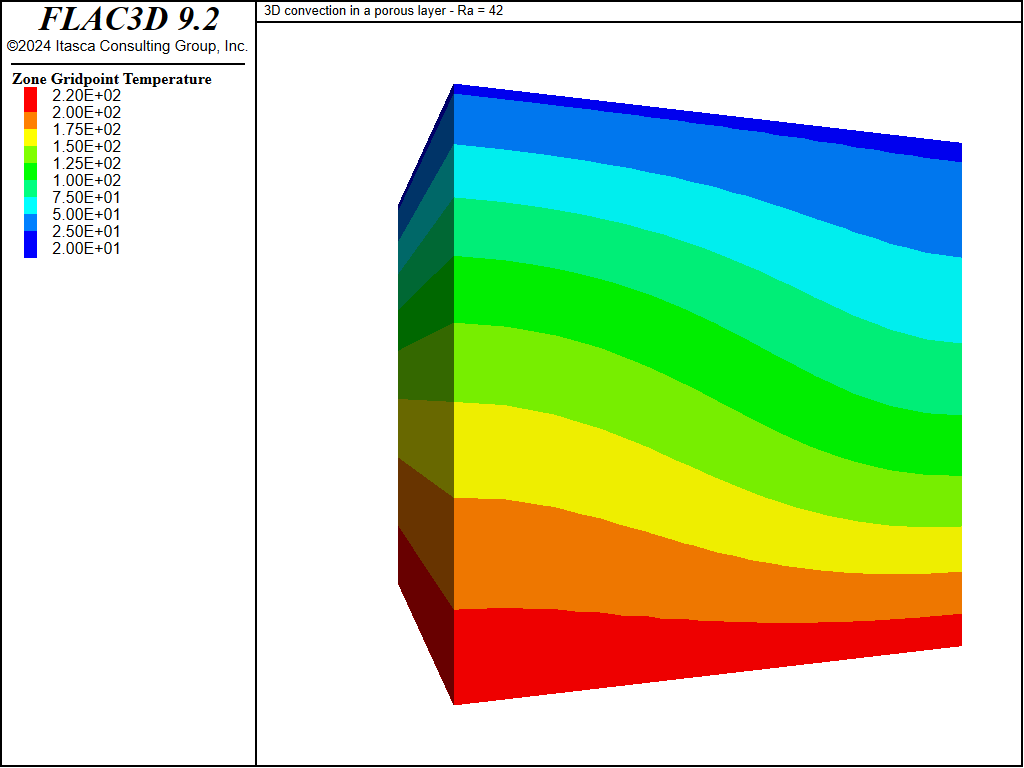
Figure 5: Temperature contours after 700 super-steps.

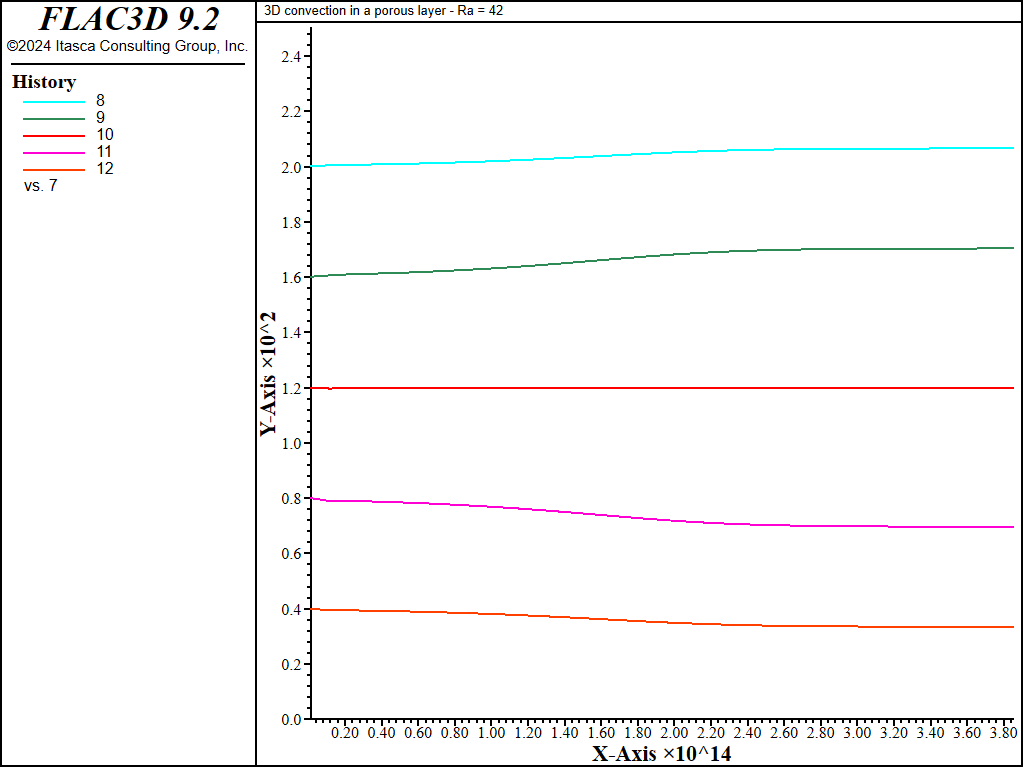
Figure 6: Evolution of temperature at 5 control points after 700 super-steps.

The simulation is continued for another 7000 super-steps. From the evolution of temperature (see Figure 7), it appears that the system has reached a steady state. The temperature contours at the end of the simulation are plotted in Figure 8. A contour plot of pore pressure at the end of the simulation is sketched in Figure 9.

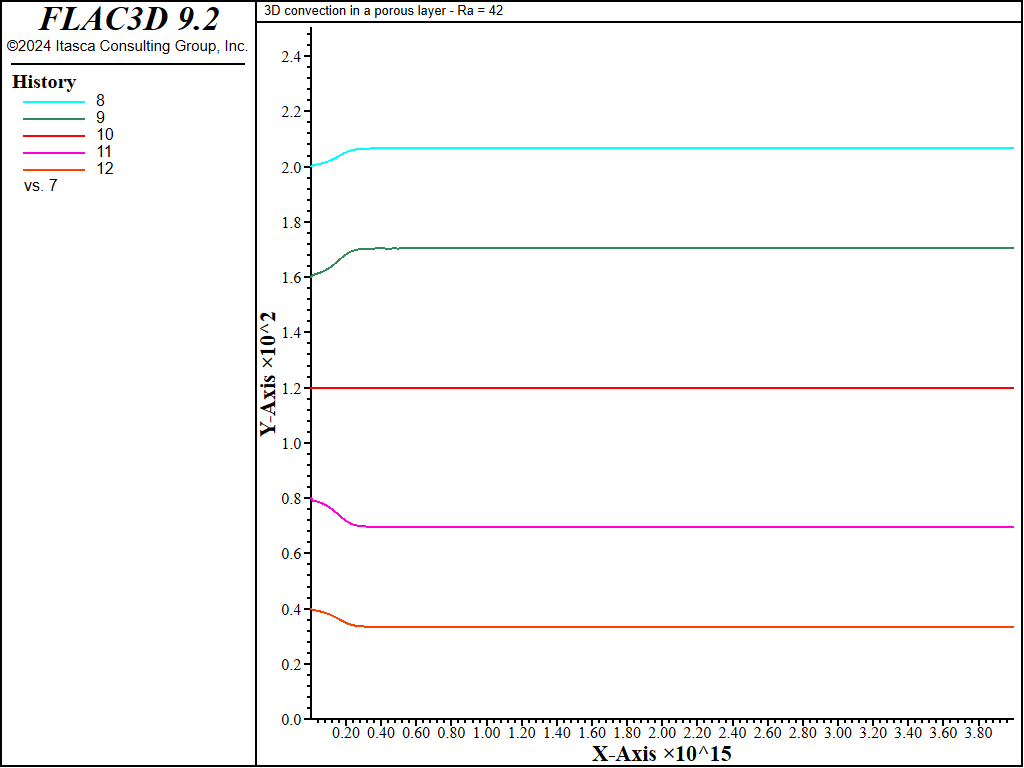
Figure 7: Evolution of temperature at 5 control points after 7700 super-steps.

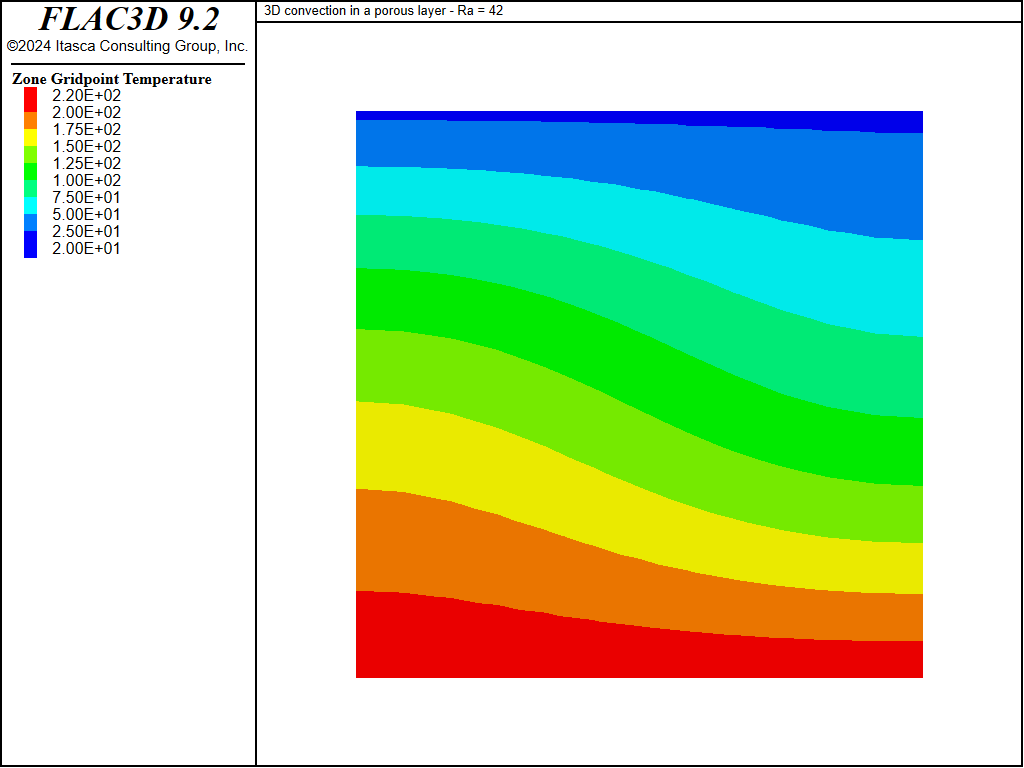
Figure 8: Temperature contours on a plane perpendicular to the x-axis after 7700 super-steps.

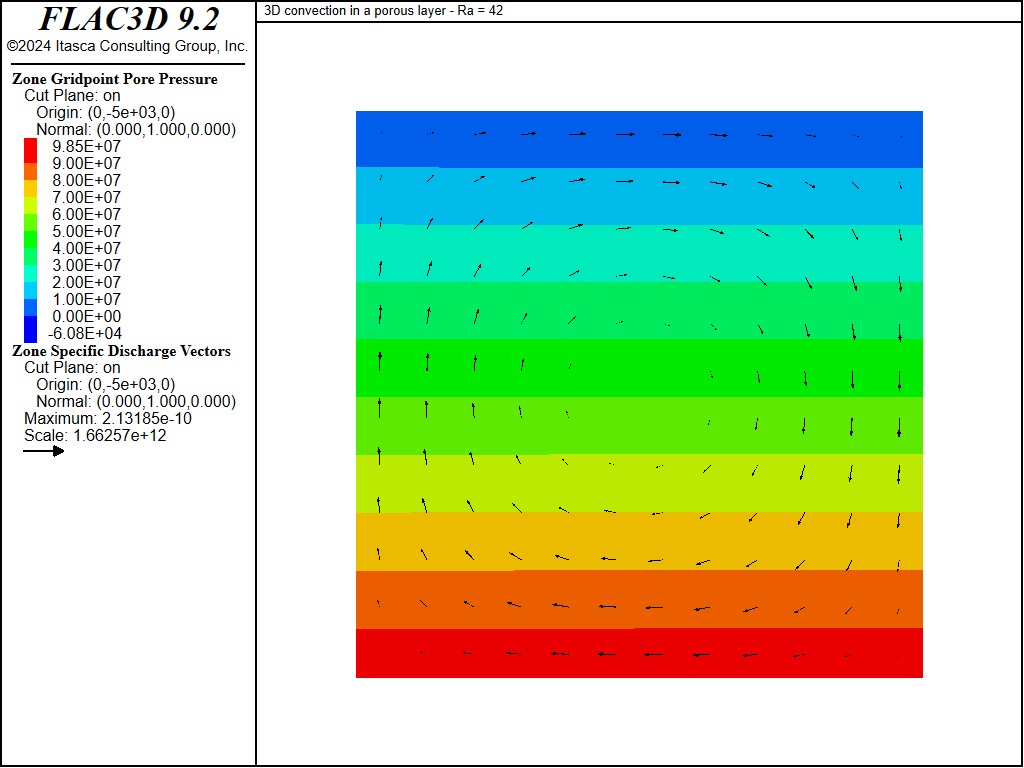
Figure 9: Pore pressure contours and flow vectors after 7700 super-steps.

The temperature contours shown in Figure 8 (2D roll in a cube at a Rayleigh number close to critical) may be compared to the two-dimensional analytical temperature contour values for mode 1, derived from linear perturbation theory (see, for example, Zhao et al. 1997) and plotted in Figure 10. The 2D analytical solution has the form

(2)\[{{T - T_0} \over {T_1 - T_0}} = C_1 {\rm cos} \bigl(\pi {x^{\ast} \over H} \bigr) {\rm sin} \bigl(\pi {y^{\ast} \over H} \bigr) + \bigl(1 - {z^{\ast} \over H} \bigr)\]

where \(x^{\ast} = x + {H \over 2}\), \(y^{\ast} = y + {H \over 2}\), \(z^{\ast} = z + {H \over 2}\) and \(C_1\) is a constant, defined here by requiring that numerical and analytical temperature values be equal at \(x^{\ast}\) = 0, \(z^{\ast} / H\) = 0.5.

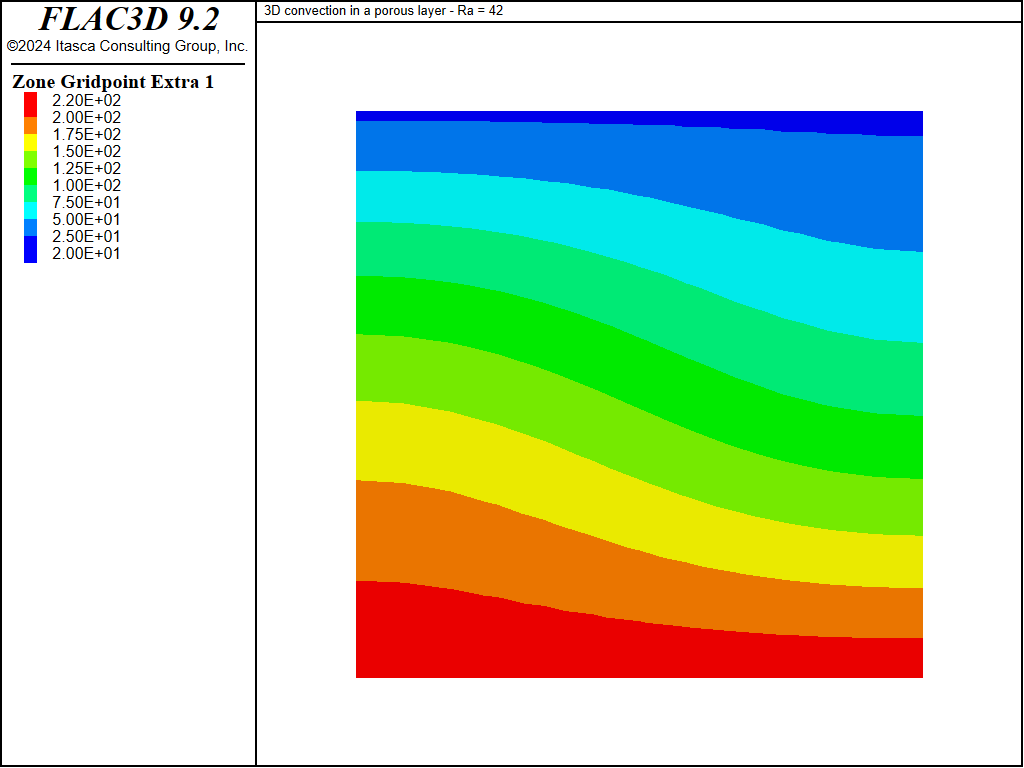
Figure 10: Temperature contours, analytical steady-state solution, Rayleigh = \(4\pi^2\).

Saturated Porous Cube with a High Rayleigh Number

For this simulation at a high Rayleigh number, we use data similar to “HRL-Convection-Cube-LowRa.dat”, except for a higher value of the fluid thermal expansion property. A small perturbation, made by tilting the gravity vector slightly in the \(x\)-direction, is done to trigger the convection cell formation.

The resulting Rayleigh number for this model is approximately 381. The multiple three-dimensional cells obtained at steady state are shown in Figure 11. The data file is listed in “HRL-Convection-Cube-HighRa.dat”.

Note that the explicit calculation mode is used at this high Rayleigh number. The implicit calculation is not as beneficial in this case.

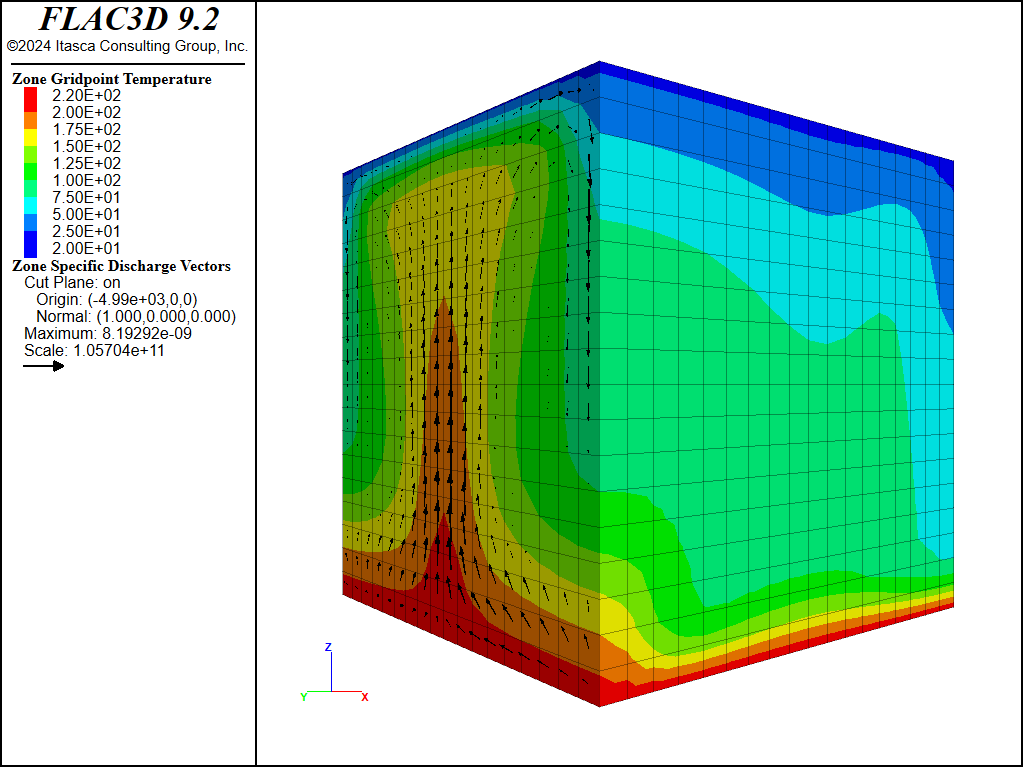
Figure 11: Steady-state temperature contours and flow vectors for a 1 × 1 × 1 box, Ra = 381.

Long Saturated Porous Box

The previous simulation is repeated, this time for a box with an aspect ratio of 8 × 1 × 1. A perturbation is done on the gravity vector, in the direction of the long dimension of the box. The cell pattern obtained at steady state is shown in Figure 12 and Figure 13. The pattern corresponds to a series of 2D rolls. The data file is listed in “HRL-Convection-LongBox.dat”.

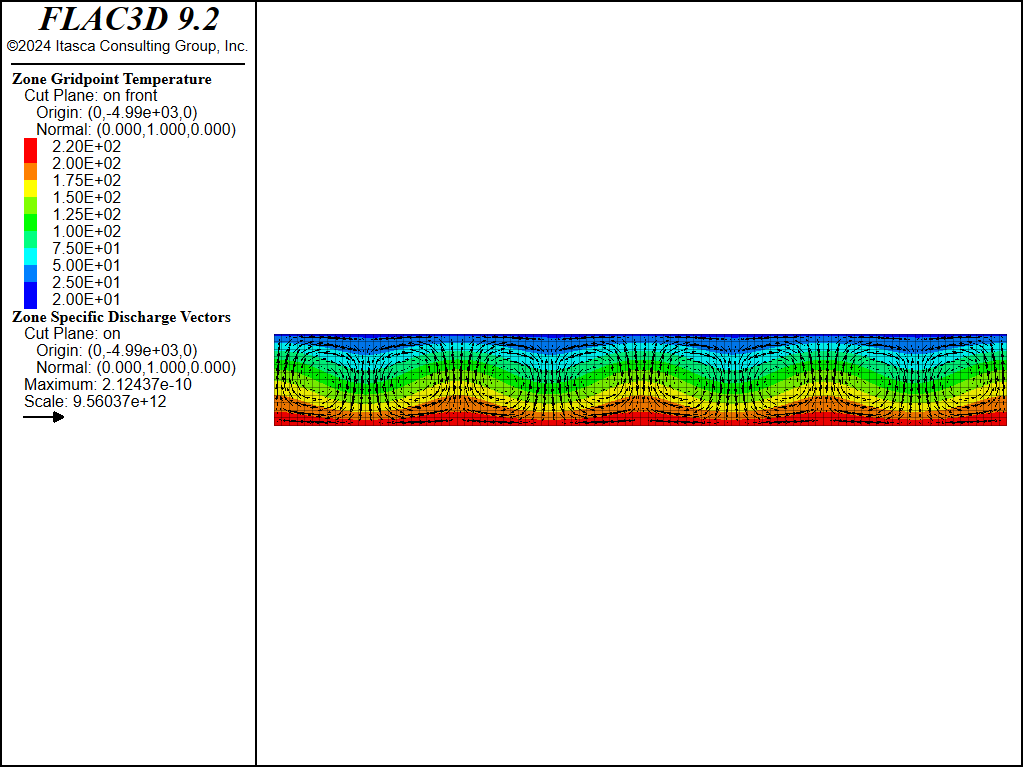
Figure 12: Steady-state temperature contours and flow vectors for 8 × 1 × 1 box, Ra = 42.

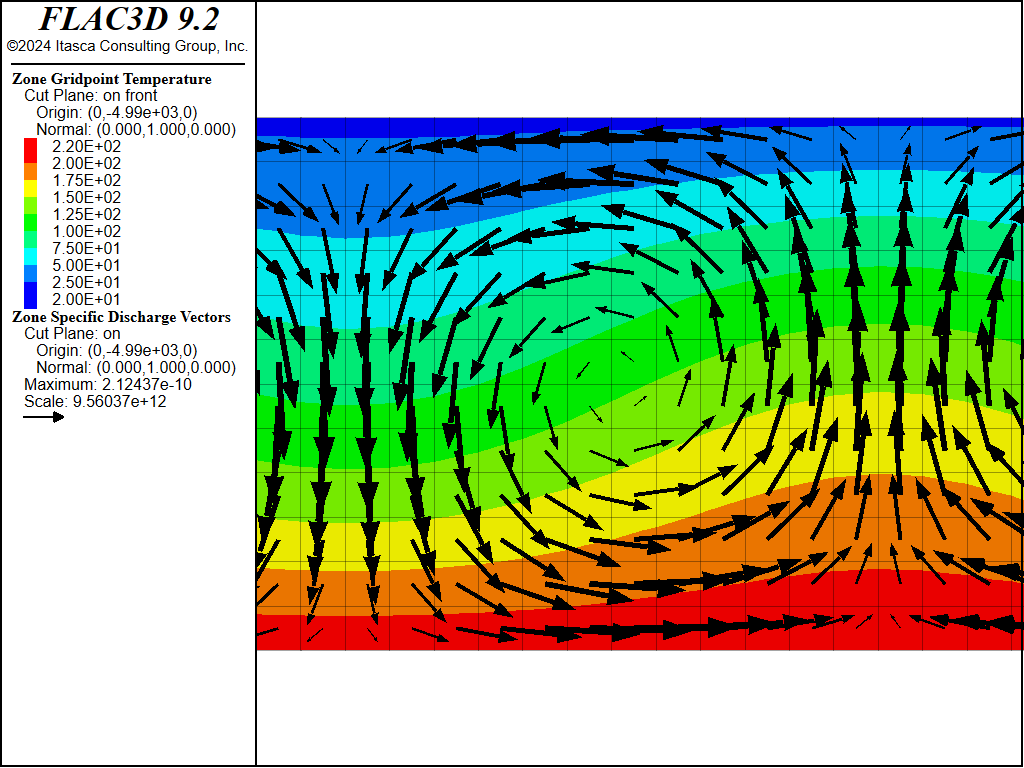
Figure 13: Close-up view of temperature contours and flow vectors for 8 × 1 × 1 box, Ra = 42.

Grid Sensitivity Analysis

To test the influence of mesh density on the steady-state results, the convection simulation is repeated for a porous box with aspect ratio 4 × 1 × 1, at a Rayleigh number of 42, using three different regular grid resolutions: coarse (24 × 6 × 6 zones); medium (48 × 12 × 12 zones); and fine (96 × 24 × 24 zones). We used the same perturbation in gravity (long box direction) for all three cases. Two-dimensional rolls are obtained for all three grid resolutions. The temperature contours and flow vectors are shown in Figure 14 to Figure 16 for coarse, medium, and fine resolution, respectively. The data file for the simulations is provided in “HRL-Convection-LongBox-Coarse.dat” to “HRL-Convection-LongBox-Fine.dat”.

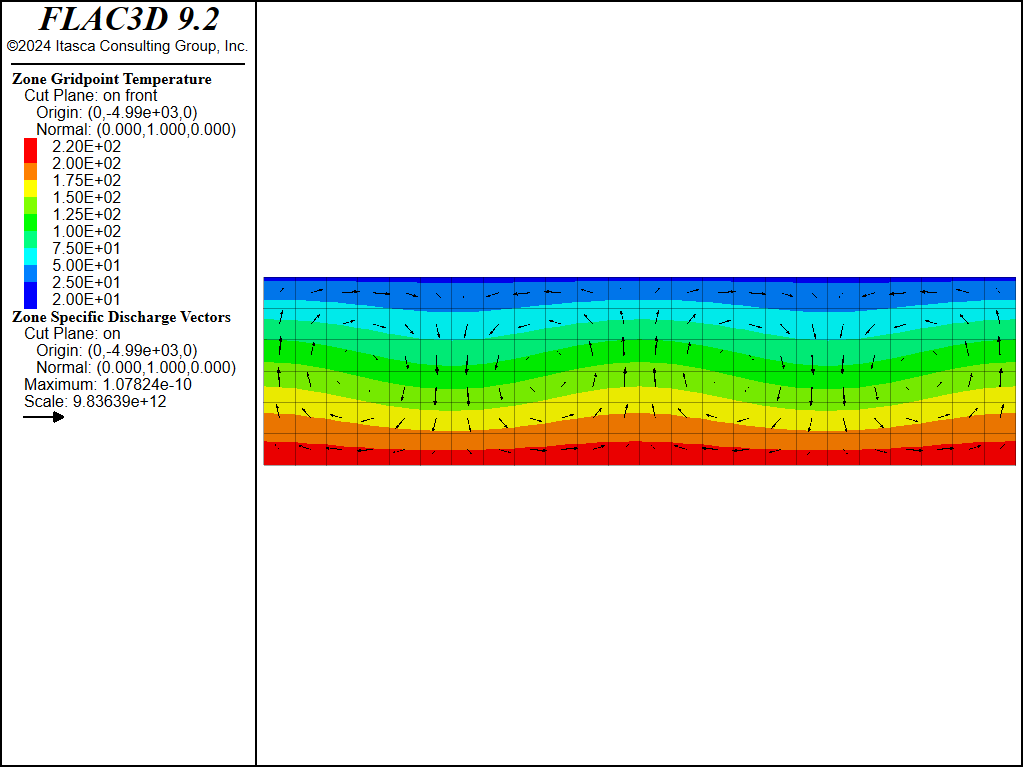
Figure 14: Steady-state temperature contours and flow vectors—coarse grid.

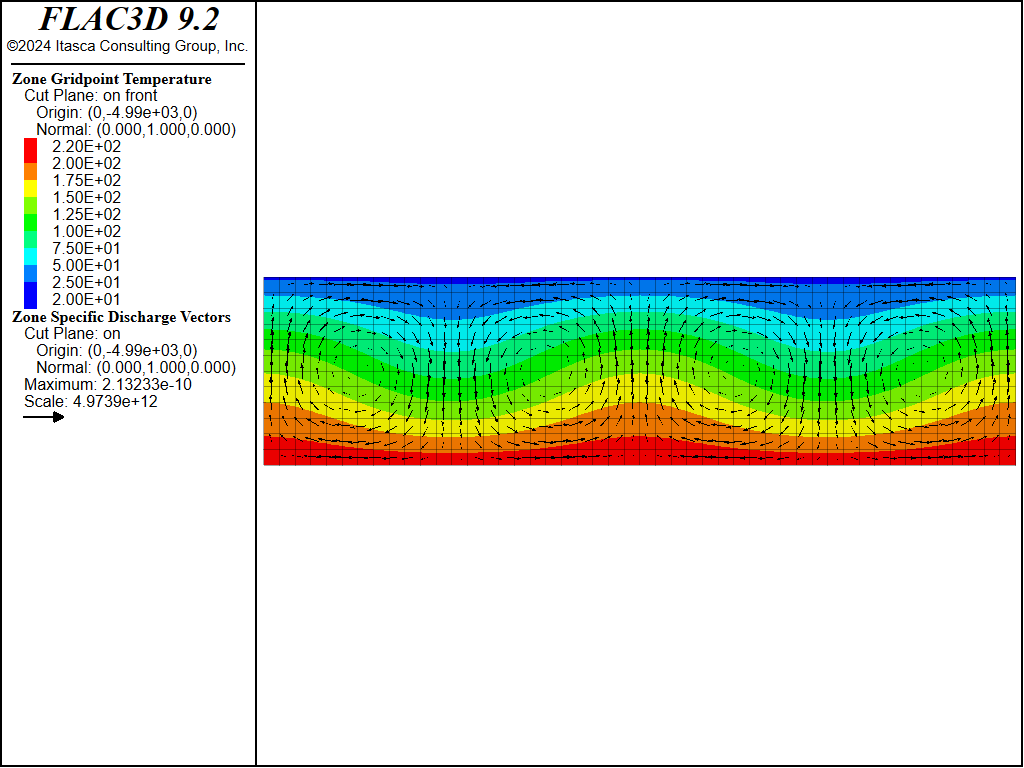
Figure 15: Steady-state temperature contours and flow vectors—medium grid.

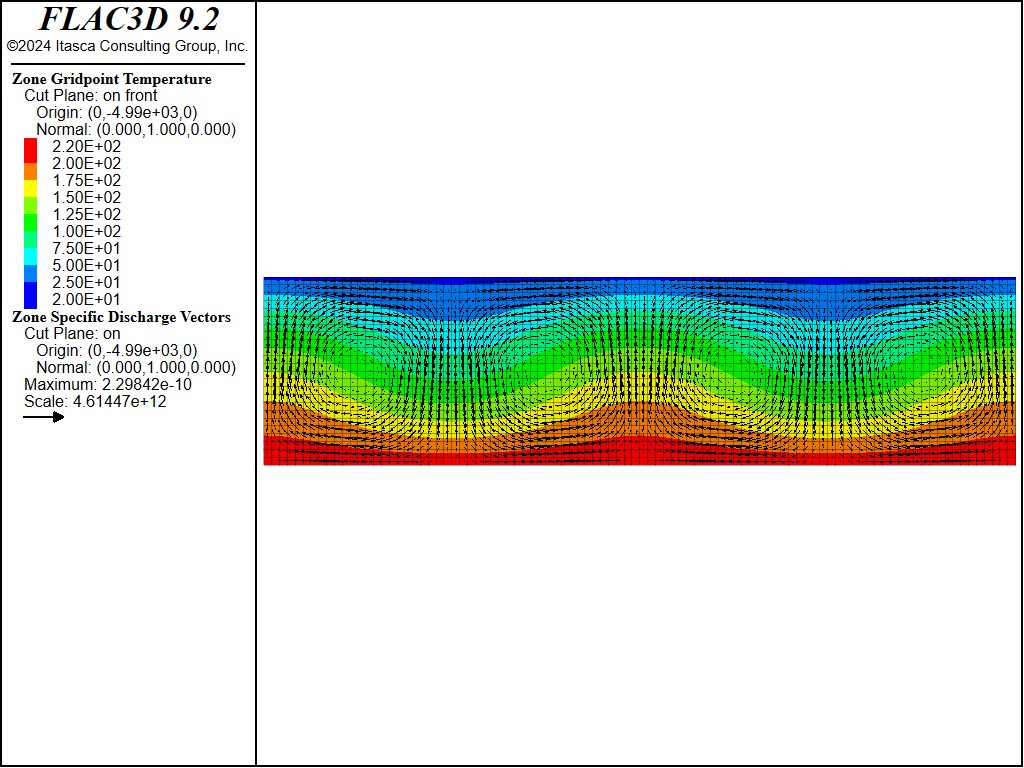
Figure 16: Steady-state temperature contours and flow vectors—fine grid.

References

Lapwood, E. R. “Convection of a Fluid in a Porous Medium,” Proc. Cambridge Philos. Soc., 44, 508-521 (1948).

Zhao, C., H. B. Mühlhaus and B. E. Hobbs. “Finite Element Analysis of Steady-State Natural Convection Problems in Fluid-Saturated Porous Media Heated from below,” Int. J. Num. & Analy. Method. Geomech., 21, 863-881 (1997).

Data Files

HortonRogersLapwoodConvection.dat

program call 'HRL-Convection-Cube-LowRa'
program call 'HRL-Convection-Cube-HighRa'
program call 'HRL-Convection-LongBox'
program call 'HRL-Convection-LongBox-Coarse'
program call 'HRL-Convection-LongBox-Medium'
program call 'HRL-Convection-LongBox-Fine'
program call 'check'

HRL-Convection-Cube-LowRa.dat

; 3D convection in a porous layer
model new
model title '3D convection in a porous layer - Ra = 42'
; --- geometry ---
zone create brick size 12 12 12 point 0 (-5e3,-5e3,-5e3) ...
                                point 1 ( 5e3,-5e3,-5e3) ...
                                point 2 (-5e3, 5e3,-5e3) ...
                                point 3 (-5e3,-5e3, 5e3)
zone face skin
; --- mechanical ---
zone cmodel assign elastic
zone property density 2000
zone gridpoint fix velocity
model mechanical active off
;    (thermal)
model configure thermal
zone thermal cmodel assign advection-conduction
zone thermal property conductivity=3.015 specific-heat=803
zone thermal property conductivity-fluid=0.6 specific-heat-fluid=4185
zone thermal property expansion-fluid=1.543e-4 expansion=7e-5
zone thermal property temperature-reference=20.0
; --- boundary conditions ---
zone face apply temperature 220 range group 'Bottom'
zone face apply temperature  20 range group 'Top'
;    (fluid)
model configure fluid-flow
zone fluid property porosity=0.1 mobility-coefficient=1e-11
zone fluid property fluid-modulus=2e5 fluid-density=1000
; --- temperature initial conditions ---
zone gridpoint initialize temperature 120 gradient (0,0,-2e-2)
; Initialize PP, including gravity and density changes due to temp
[global depth = 5e3 - gp.pos(::gp.list)->z]
[gp.pp(::gp.list) ::= 10000*depth*(1-(1.543e-4*depth/100))

; --- histories ---
history interval 20
model history fluid time-total
zone history pore-pressure position (-4e3,-4e3,-4e3)
zone history pore-pressure position (-2e3,-2e3,-2e3)
zone history pore-pressure position (   0,   0,   0)
zone history pore-pressure position ( 2e3, 2e3, 2e3)
zone history pore-pressure position ( 4e3, 4e3, 4e3)
model history thermal time-total
zone history temperature   position (-4e3,-4e3,-4e3)
zone history temperature   position (-2e3,-2e3,-2e3)
zone history temperature   position (   0,   0,   0)
zone history temperature   position ( 2e3, 2e3, 2e3)
zone history temperature   position ( 4e3, 4e3, 4e3)

; --- conduction solution ---
model save 'cube-lowRa-cd'

; --- convection ---
model gravity 0.05 0 -10 ; Breaking symmetry perturbation
model thermal timestep maximum 1e12
zone fluid implicit servo on ; error 1e-4
model fluid follower on 

model solve time-total 1e13 synchronize
model save 'cube-lowRa-hf'

model gravity 10 ; Restore normal gravity
model solve time-total 3e13 synchronize
model save 'cube-lowRa-he'

model solve time-total 6e13 synchronize
model save 'cube-lowRa-h4'  

model solve time-total 4e14 synchronize
model save 'cube-lowRa-h10' 

model solve time-total 4e15 synchronize
model save 'cube-lowRa-h40' 
program return

HRL-Convection-Cube-HighRa.dat

model new
model title '3D convection in a porous layer - Ra = 381'
; --- geometry ---
zone create brick size 18 18 18 point 0 (-5e3,-5e3,-5e3) ...
                                point 1 ( 5e3,-5e3,-5e3) ...
                                point 2 (-5e3, 5e3,-5e3) ...
                                point 3 (-5e3,-5e3, 5e3)
zone face skin
; --- mechanical ---
zone cmodel assign elastic
zone property density 2000
zone gridpoint fix velocity
model mechanical active off
;    (thermal)
model configure thermal
zone thermal cmodel assign advection-conduction
zone thermal property conductivity=3.015 specific-heat=803
zone thermal property conductivity-fluid=0.6 specific-heat-fluid=4185
zone thermal property expansion-fluid=1.4e-3 expansion=7e-5
zone thermal property temperature-reference=20.0
; --- boundary conditions ---
zone face apply temperature 220 range group 'Bottom'
zone face apply temperature  20 range group 'Top'
;    (fluid)
model configure fluid-flow
zone fluid property porosity=0.1 mobility-coefficient=1e-11
zone fluid property fluid-modulus=2e5 fluid-density=1000
; --- initial conditions ---
zone gridpoint initialize temperature 120 gradient (0,0,-2e-2)
; Initialize PP, including gravity and density changes due to temp
[global depth = 5e3 - gp.pos(::gp.list)->z]
[gp.pp(::gp.list) ::= 10000*depth*(1-(1.4e-3*depth/100))
; --- convection ---
model fluid follower on 

; Timestep needs to be reduced for stability
model fluid timestep fix 2e9 
model thermal timestep fix 2e10

history interval 1
model history timestep

model gravity (0.05,0,-10) ; Perturb with gravity
model solve time-total 1e13 synchronize
model save 'cube-highRa-hf'

model gravity 10 ; --- reset gravity
model solve time-total 2e13 synchronize
model save 'cube-highRa-he'

model solve time-total 8e13 synchronize
model save 'cube-highRa-h10'
program return

HRL-Convection-LongBox.dat

model new
model title '3D convection in a long porous box - Ra = 42 ? medium grid'
; --- geometry ---
zone create brick size 96 12 12 point 0 -4e4 -5e3 -5e3 ...
                                point 1  4e4 -5e3 -5e3 ...
                                point 2 -4e4  5e3 -5e3 ...
                                point 3 -4e4 -5e3  5e3
zone face skin 
; --- mechanical ---
zone cmodel assign elastic
zone property density 2000
zone gridpoint fix velocity
model mechanical active off
;    (thermal)
model configure thermal
zone thermal cmodel assign advection-conduction
zone thermal property conductivity=3.015 specific-heat=803
zone thermal property conductivity-fluid=0.6 specific-heat-fluid=4185
zone thermal property expansion-fluid=1.543e-4 expansion=7e-5
zone thermal property temperature-reference=20.0
; --- boundary conditions ---
zone face apply temperature 220 range group 'Bottom'
zone face apply temperature  20 range group 'Top'
;    (fluid)
model configure fluid-flow
zone fluid property porosity=0.1 mobility-coefficient=1e-11
zone fluid property fluid-modulus=2e5 fluid-density=1000
; --- temperature initial conditions ---
zone gridpoint initialize pore-pressure 0.5e8 gradient 0 0 -1e4
; Initialize PP, including gravity and density changes due to temp
[global depth = 5e3 - gp.pos(::gp.list)->z]
[gp.pp(::gp.list) ::= 10000*depth*(1-(1.543e-4*depth/100))
; --- histories ---
history interval 20
model history fluid time-total
zone history pore-pressure position (-4e3,-4e3,-4e3)
zone history pore-pressure position (-2e3,-2e3,-2e3)
zone history pore-pressure position (   0,   0,   0)
zone history pore-pressure position ( 2e3, 2e3, 2e3)
zone history pore-pressure position ( 4e3, 4e3, 4e3)
model history thermal time-total
zone history temperature   position (-4e3,-4e3,-4e3)
zone history temperature   position (-2e3,-2e3,-2e3)
zone history temperature   position (   0,   0,   0)
zone history temperature   position ( 2e3, 2e3, 2e3)
zone history temperature   position ( 4e3, 4e3, 4e3)

model save 'longBox0-cd'

; --- convection ---
model gravity (0.05,0,-10) ; perturbation
;zone thermal implicit servo error 1e-5
zone fluid implicit servo on ; error 1e-4
model fluid follower on 

model solve thermal time-total 1e13 synchronize
model save 'longBox0-hf'

; reset gravity to vertical
model gravity 10
model solve thermal time-total 3e13 synchronize
model save 'longBox0-he'

model solve thermal time-total 1e15 synchronize
model save 'longBox0-h40'

program return

HRL-Convection-LongBox-Coarse.dat

model new
model title '3D convection in a porous 4x1x1 box - Ra = 42 - coarse'
; --- geometry ---
zone create brick size 24 6 6 point 0 -2e4 -5e3 -5e3 point 1  2e4 -5e3 -5e3 ...
                              point 2 -2e4  5e3 -5e3 point 3 -2e4 -5e3  5e3
zone face skin                              
; --- mechanical
zone cmodel assign elastic
zone property density 2000
zone gridpoint fix velocity
model mechanical active off
;    (thermal)
model configure thermal
zone thermal cmodel assign advection-conduction
zone thermal property conductivity=3.015 specific-heat=803
zone thermal property conductivity-fluid=0.6 specific-heat-fluid=4185
zone thermal property expansion-fluid=1.543e-4 expansion=7e-5
zone thermal property temperature-reference=20.0
; --- boundary conditions ---
zone face apply temperature 220 range group 'Bottom'
zone face apply temperature  20 range group 'Top'
;    (fluid)
model configure fluid-flow
zone fluid property porosity=0.1 mobility-coefficient=1e-11
zone fluid property fluid-modulus=2e5 fluid-density=1000
; --- temperature initial conditions ---
zone gridpoint initialize temperature 120 gradient 0 0 -2e-2
; Initialize PP, including gravity and density changes due to temp
[global depth = 5e3 - gp.pos(::gp.list)->z]
[gp.pp(::gp.list) ::= 10000*depth*(1-(1.543e-4*depth/100))
; --- convection ---
model gravity (0.05,0,-10) ; perturbation
;zone thermal implicit servo error 1e-6
zone fluid implicit servo on ; error 1e-6
model fluid follower on

model solve thermal time-total 2e13 synchronize
model save 'longBox-coarse-hf'

model gravity 10 ; reset gravity to vertical
model solve thermal time-total 4e13 synchronize
model save 'longBox-coarse-he'

model solve thermal time-total 3e15 synchronize
model save 'longBox-coarse-h30'
program return

HRL-Convection-LongBox-Medium.dat

model new
model title '3D convection in a porous 4x1x1 box - Ra = 42 - medium'
; --- geometry ---
zone create brick size 48 12 12 point 0 -2e4 -5e3 -5e3 point 1  2e4 -5e3 -5e3 ...
                                point 2 -2e4  5e3 -5e3 point 3 -2e4 -5e3  5e3
zone face skin                              
; --- mechanical
zone cmodel assign elastic
zone property density 2000
zone gridpoint fix velocity
model mechanical active off
;    (thermal)
model configure thermal
zone thermal cmodel assign advection-conduction
zone thermal property conductivity=3.015 specific-heat=803
zone thermal property conductivity-fluid=0.6 specific-heat-fluid=4185
zone thermal property expansion-fluid=1.543e-4 expansion=7e-5
zone thermal property temperature-reference=20.0
; --- boundary conditions ---
zone face apply temperature 220 range group 'Bottom'
zone face apply temperature  20 range group 'Top'
;    (fluid)
model configure fluid-flow
zone fluid property porosity=0.1 mobility-coefficient=1e-11
zone fluid property fluid-modulus=2e5 fluid-density=1000
; --- temperature initial conditions ---
zone gridpoint initialize temperature 120 gradient 0 0 -2e-2
; Initialize PP, including gravity and density changes due to temp
[global depth = 5e3 - gp.pos(::gp.list)->z]
[gp.pp(::gp.list) ::= 10000*depth*(1-(1.543e-4*depth/100))
; --- convection ---
model gravity (0.05,0,-10) ; perturbation
zone thermal implicit servo error 1e-5
zone fluid implicit servo on ; error 1e-4
model fluid follower on

model solve thermal time-total 2e13 synchronize
model save 'longBox-medium-hf'

model gravity 10 ; reset gravity to vertical
model solve thermal time-total 4e13 synchronize
model save 'longBox-medium-he'

model solve thermal time-total 3e15 synchronize
model save 'longBox-medium-h30'
program return

HRL-Convection-LongBox-Fine.dat

model new
model title '3D convection in a porous 4x1x1 box - Ra = 42 - fine'
; --- geometry ---
zone create brick size 96 24 24 point 0 -2e4 -5e3 -5e3 point 1  2e4 -5e3 -5e3 ...
                              point 2 -2e4  5e3 -5e3 point 3 -2e4 -5e3  5e3
zone face skin                              
; --- mechanical
zone cmodel assign elastic
zone property density 2000
zone gridpoint fix velocity
model mechanical active off
;    (thermal)
model configure thermal
zone thermal cmodel assign advection-conduction
zone thermal property conductivity=3.015 specific-heat=803
zone thermal property conductivity-fluid=0.6 specific-heat-fluid=4185
zone thermal property expansion-fluid=1.543e-4 expansion=7e-5
zone thermal property temperature-reference=20.0
; --- boundary conditions ---
zone face apply temperature 220 range group 'Bottom'
zone face apply temperature  20 range group 'Top'
;    (fluid)
model configure fluid-flow
zone fluid property porosity=0.1 mobility-coefficient=1e-11
zone fluid property fluid-modulus=2e5 fluid-density=1000
; --- temperature initial conditions ---
zone gridpoint initialize temperature 120 gradient 0 0 -2e-2
; Initialize PP, including gravity and density changes due to temp
[global depth = 5e3 - gp.pos(::gp.list)->z]
[gp.pp(::gp.list) ::= 10000*depth*(1-(1.543e-4*depth/100))
; --- convection ---
model gravity (0.1,0,-10) ; perturbation
zone fluid implicit servo on 
model fluid follower on

model solve thermal time-total 2e13 synchronize
model save 'longBox-fine-hf'

model gravity 10 ; reset gravity to vertical
model solve thermal time-total 4e13 synchronize
model save 'longBox-fine-he'

model solve thermal time-total 4e14 synchronize
model save 'longBox-fine-h30'
program return