FLAC3D Theory and Background • Constitutive Models

Drained Triaxial Compression Test with Plastic-Hardening Model

Note

To view this project in FLAC3D, use the menu command Help ? Examples…. Choose “ConstitutiveModels/ DrainedTriaxialPlasticHardening” and select “DrainedTriaxialPlasticHardening.f3dprj” to load. The project’s main data file is shown at the end of this example.

Triaxial tests on dense, medium, and loose sand are simulated using the Plastic-Hardening (PH) model. The model properties are listed in Table 1. This example does not consider yielding on the cap; therefore, the default value \(OCR\) = 100 is used. The initial stress state is isotropic, with mean pressure equal to 100 kPa. The cell pressure is kept constant during the test, the base of the model is fixed in the axial (y-) direction, and an axial velocity of 10^-6 m/step is applied at the top of the model. In addition, three unloading/reloading excursions are performed.

Table 1: Plastic-Hardening Model Properties

Parameter	Dense	Medium	Loose
\(E^{ref}_{50}\) (kPa)	4.0e4	3.0e4	2.0e4
\(\phi\)	40	35	30
\(\psi\)	10	5	0
\(K_{nc}\)	0.36	0.43	0.50
\(c\) (kPa)		0 or 20
\(p_{ref}\) (kPa)		100
\(m\)		0.5
\(\sigma^{ini}_{1 \sim 3}\) (kPa)		-100
\(OCR\)		100
\(e_{max}\)		1.02

A plot of deviatoric stress versus axial strain is shown in Figure 1, which reveals the hyperbolic behavior. The unloading-reloading paths are also shown in the figure. The plot of volumetric strain versus axial strain is shown in Figure 2. The dilatancy of the denser sands is clearly represented. The smooth evolution of the dilation angle when the void ratio is approaching the critical state occurs as a result of the dilation smoothing technique implemented in the model logic.

The comparable results for the simulation with cohesion set to 20 kPa are shown in Figure 3 and Figure 4. It is seen from Figure 3 that the initial stiffness of cohesive sand is higher than for the sand without cohesion. Similarly, deviatoric stress at failure is higher for the cohesive material.

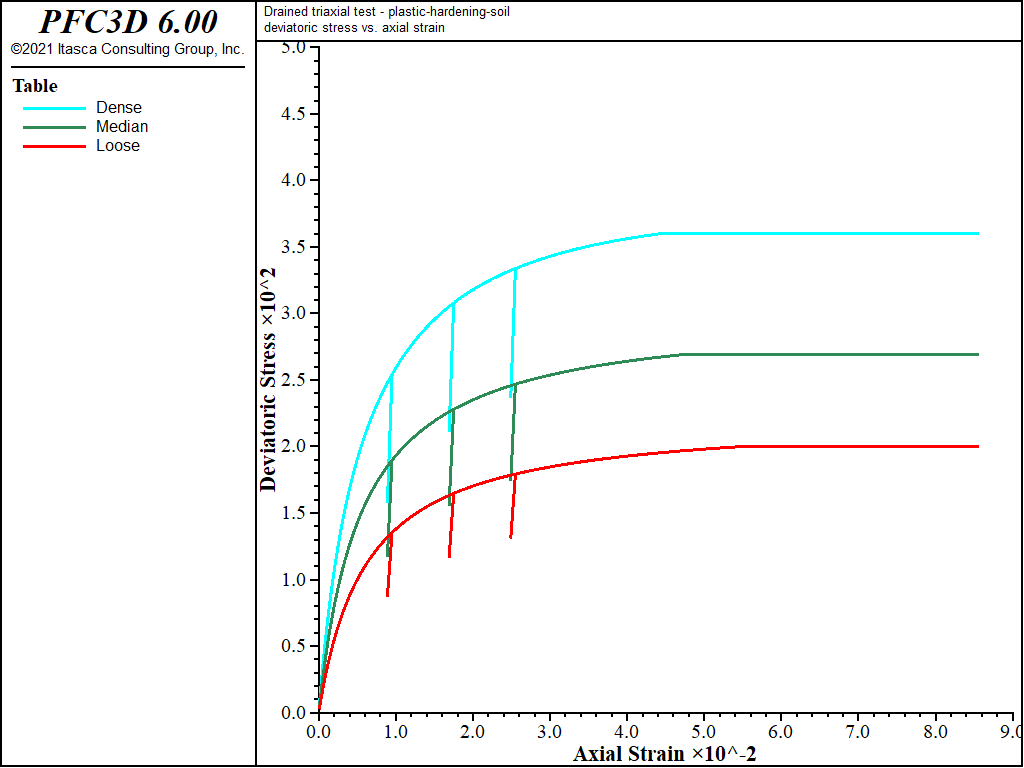
Figure 1: \(\mid \sigma_1 - \sigma_3 \mid\) (in kPa) versus axial strain for dense, medium, and loose sand—constant dilation.

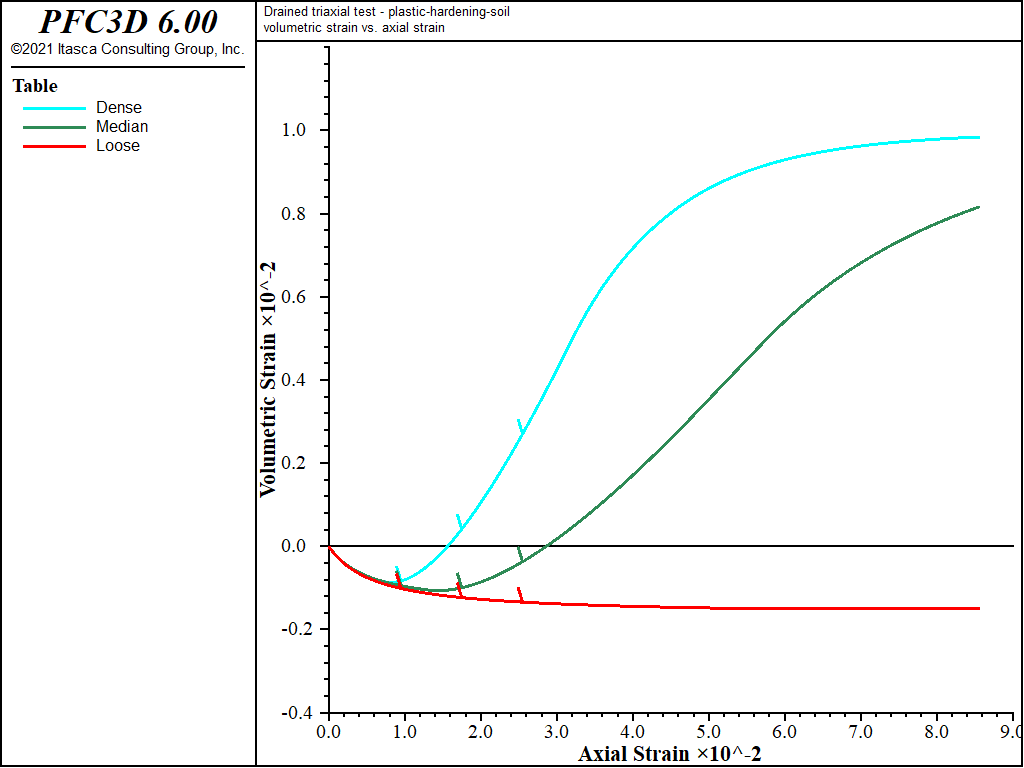
Figure 2: Volumetric strain versus axial strain for dense, medium, and loose sand—constant dilation.

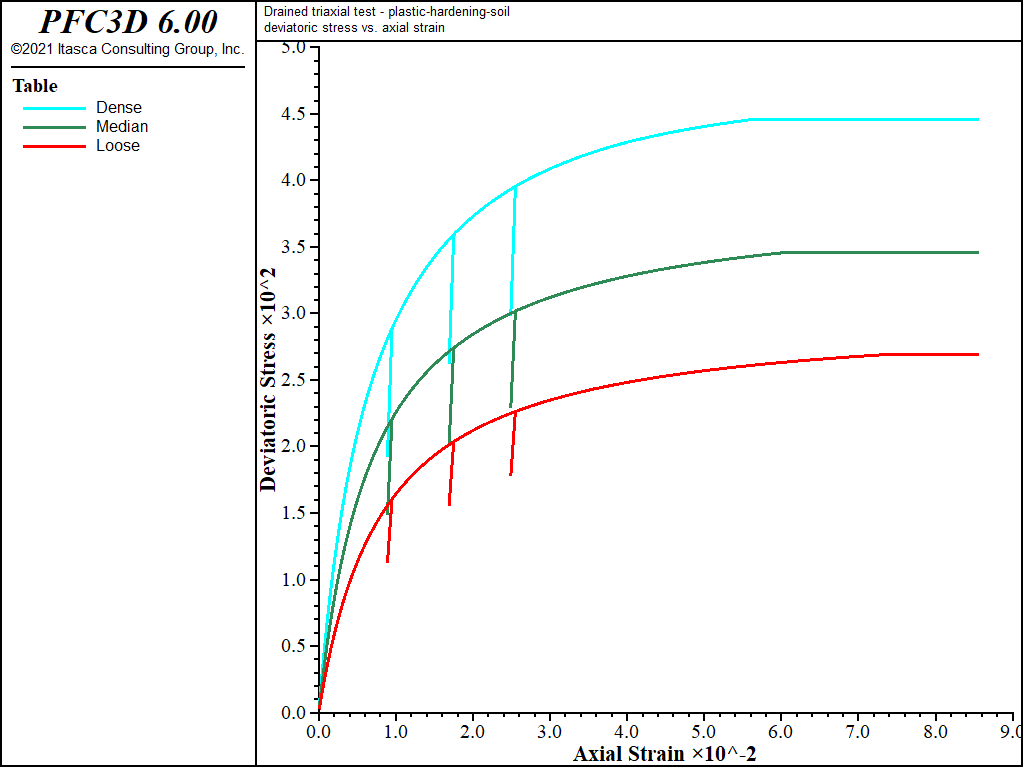
Figure 3: \(\mid \sigma_1 - \sigma_3 \mid\) (in kPa) versus axial strain for dense, medium, and loose sand—constant dilation (dilation = 20 kPa).

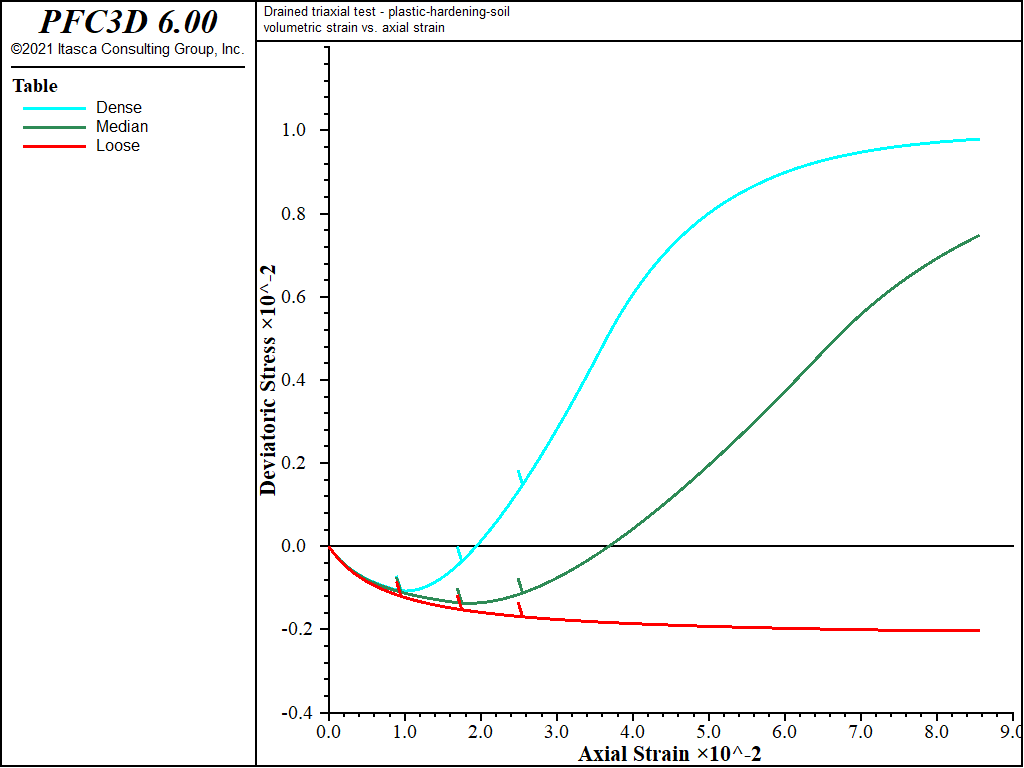
Figure 4: Volumetric strain versus axial strain for dense, medium, and loose sand—constant dilation (dilation = 20 kPa).

Data File

; Drained Triaxial Tests - Constant Dilation
model title "Drained triaxial test - Plastic Hardening model"
model largestrain off

zone create brick size 1 1 1
zone face skin
zone cmodel assign plastic-hardening
zone initialize stress xx -100. yy -100. zz -100.
zone property density 1000 pressure-reference=100. exponent=0.5 void-maximum=1.02
zone property stiffness-50-reference=@E50ref friction=@fric dilation=@dila cohesion=@coh coefficient-normally-consolidation=@knc
zone property stress-1-effective=-100. stress-2-effective=-100. stress-3-effective=-100.
zone face apply stress-norm -100. range group 'East' or 'West'
zone face apply stress-norm -100. range group 'North' or 'South'
zone face apply velocity-z 0 range group 'Bottom'
zone face apply velocity-z -1e-6 range group 'Top'
;
fish define ph_q
    local z = zone.head
    global ph_q =  zone.stress.xx(z) - zone.stress.zz(z)
    global vsi = zone.strain.vol.inc(z)
end
;
zone history displacement-z position (1,1,1)
fish history @ph_q
fish history @vsi
history interval 100
;
fish define trip
    loop local i (1,3)
        command
            zone face apply velocity-z -2e-6 range group 'Top'
model step 4000
            zone face apply velocity-z  2e-7 range group 'Top'
model step 3000
            zone face apply velocity-z -2e-7 range group 'Top'
model step 3000
        end_command
    end_loop
end
model step 1500
@trip
zone face apply velocity-z -2e-6 range group 'Top'
model step 30000
;
history export 2 vs 1 reverse table 'deviatoricStress'
history export 3 vs 1 reverse table 'volumetricStrain'
table 'deviatoricStress' export [string.build('deviatoricStress%1', _IChoice)] truncate 
table 'volumetricStrain' export [string.build('volumetricStrain%1', _iChoice)] truncate
;
return