Burger’s Contact Model: Stress Relaxation

	Problem Resources
Data Files	Project: Open “StressRelax.p2prj” in PFC2D; “StressRelax.p3prj” in PFC3D [1]

Problem Statement

The Burger’s Model is exercised with a simple system consisting of two balls fixed with a non-zero initial overlap. The time-decay of the normal force is compared against the expected analytical solution.

Analytical Solution

Consider the stress relaxation condition (i.e., the response of the contact force to the unit displacement). For convenience, eq. (5) in the Burger’s model description is reshown below:

(1)\[f = a_1 \dot{f} + a_2 \ddot{f} = b_1 \dot{u} + b_2 \ddot{u}\]

where:

(2)\[\begin{split}a_1 &= \frac{C_k}{K_k} + C_m \left( \frac{1}{K_k} + \frac{1}{K_m} \right) \\ a_2 &= \frac{C_k C_m}{K_k K_m} \\ b_1 &= \pm C_m \\ b2 &= \pm \frac{C_k C_m}{K_k}\end{split}\]

with symbols \(\pm\) and \(\mp\) corresponding to the cases of normal and shear direction, respectively (For example, \(\pm\) means \(+\) for normal direction and \(-\) for shear direction.).

The Laplace transform of (1) is given by (3) under the initial condition of \(\dot{u} = u = 0\), \(\dot{f} = f = 0\).

(3)\[\left( 1+ a_1 s + a_2 s^2 \right) F(s) = \left( b_1 s + b_2 s^2 \right) U(s)\]

where \(U(s) = \mathcal{L}[u(t)]\) and \(F(s) = \mathcal{L}[f(t)]\).

The transfer function of the system is given by:

(4)\[G(s) = \frac{F(s)}{U(s)} = \frac{b_1 s + b_2 s^2 }{1+ a_1 s + a_2 s^2}\]

For the unit input \(u(t)= 1\) therefore \(U(s) = 1/s\), the response is given by:

(5)\[F(s) = G(s) U(s) = \frac{b_1 s + b_2 s^2 }{1+ a_1 s + a_2 s^2} \frac{1}{s} = \frac{b_1 + b_2 s }{1+ a_1 s + a_2 s^2}\]

which is expressed by:

(6)\[F(s) = \frac{A_1}{s - z_1} + \frac{A_2}{s-z_2}\]

where \(z_1\) and \(z_2\) are the roots of the quadratic equation \(a_2 s^2 + a_1 s + 1 = 0\), and

(7)\[\begin{split}A_1 = \frac{b_2 z_1 + b_1}{a_2 \left( z_1 - z_2 \right)} \\ A_2 = \frac{b_2 z_2 + b_1}{a_2 \left( z_2 - z_1 \right)}\end{split}\]

Therefore, the analytical solution of time domain for inputting a unit displacement \(u(t)=1\) is given by:

(8)\[f(t) = A_1 \exp(z_1 t) + A_2 \exp(z_2 t)\]

PFC Model

Numerical simulations are conducted in PFC2D and PFC3D with the datafiles listed in here. The two systems are identical; they consists in two balls of equal radius of 0.05 and density 2600 kg/m³ , with an initial overlap (i.e. a step input) of \(u(t=0) = 0.01\). The only difference resides in the shape of the particles: spheres in 3D and unit-thickness disks in 2D, which reflects in the mass and timesteps in the systems being different.

Figures 1 and 2 show the time-decay of the normal force calculated by PFC, compared to the analytical solution. In both models, the numerical solution shows that the contact force exponentially decreases as time increases, which coincides with the analytical solution shown by the blue dashed line in the figures.

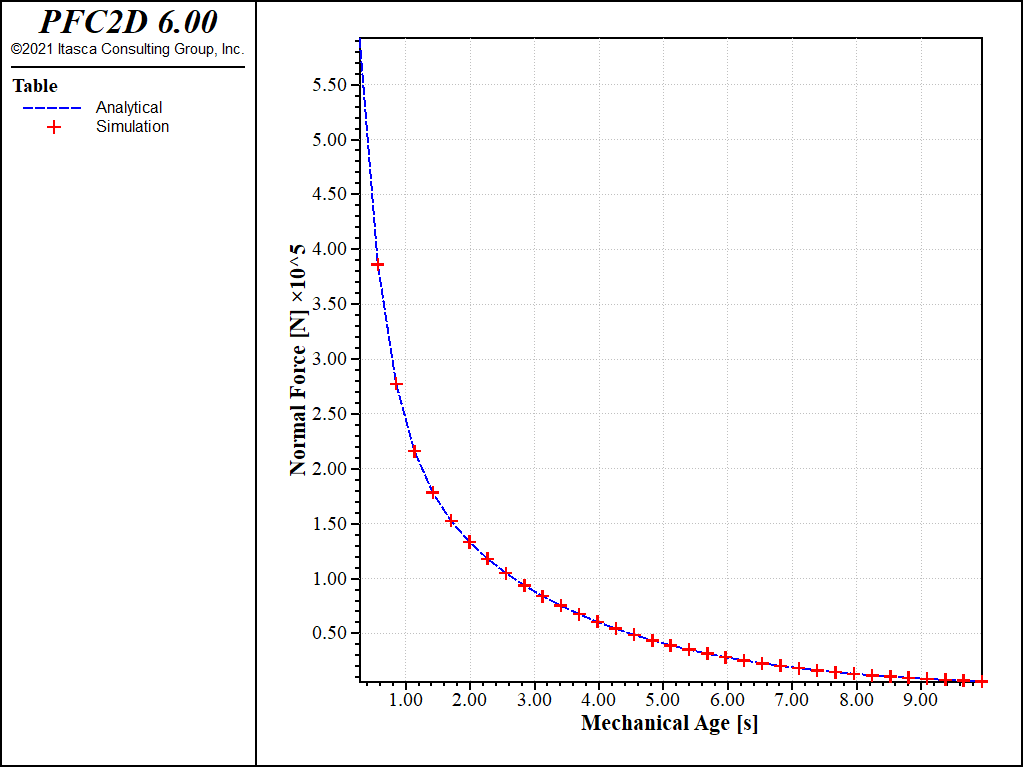
Figure 1: Time history of normal contact force of Burger’s model. The simulation results are shown in red marks, the analytical solution with the blue dashed line (2D model).

Figure 2: Time history of normal contact force of Burger’s model. The simulation results are shown in red marks, the analytical solution with the blue dashed line (3D model).

Endnote

[1]

This file may be found in PFC2D or PFC3D under the “verification_problems/contactmodels/burger/stress_relaxation” folder in the Examples dialog (Help —> Examples on the menu). If this entry does not appear, please copy the application data to a new directory. (Use the menu commands Tools —> Copy App Data …. See the “Copy Application Data” section for details.)