Mohr-Coulomb Joint Model In 3DEC

The Coulomb slip model provides a linear representation of joint stiffness and yield limit, and is based upon elastic stiffness, frictional, cohesive, and tensile strength properties, and dilation characteristics common to rock joints. The model (optionally) simulates displacement-weakening of the joint by loss of cohesive and tensile strength at the onset of shear or tensile failure.

Formulations

Shear and normal stresses on a joint develop as in the elastic model until the stress reaches the peak strength. The peak shear stress is given by:

(1)\[S_F^{peak} = c + \sigma_n \tan\phi\]

where \(c\) is the cohesion, \(\sigma_n\) is the normal stress and \(\phi\) is the friction angle.

When the peak shear strength is exceeded, the shear strength drops instantaneously to the residual shear strength. The shear stress can then not exceed the residual strength. The residual strength is given by:

(2)\[S_F^{res} = c_{res} + \sigma_n \tan\phi_{res}\]

where \(c_{res}\) is the residual cohesion, and \(\phi_{res}\) is the residual friction angle.

By default in 3DEC, \(c_{res} = 0\) and \(\phi_{res} = \phi\).

Typical shear stress/shear displacement behavior is shown in Figure 1 and the failure envelopes for default values of residual cohesion and friction are shown in Figure 2.

Figure 1: 3DEC Mohr-Coulomb joint shear stress versus shear displacement behavior.

Figure 2: 3DEC Joint Mohr-Coulomb shear failure criterion.

The tensile strength is a single user-defined value, \(T_f\). The normal stress on a joint decreases as the joint opens (assuming compression is positive) according to the normal stiffness as described for the elastic model. The normal stress is limited by the tensile strength. When the tensile strength is exceeded, the normal stress on the joint becomes equal to the residual tensile strength (\(T_f^{res}\)). By default, the residual tensile strength is 0. Typical normal stress behavior on a Mohr-Coulomb joint is shown in Figure 3.

Figure 3: 3DEC Mohr-Coulomb joint normal stress versus normal displacement behavior.

After shear strength has been exceeded, it is possible for the joint to dilate with continued shearing. The tangent of the dilation angle, \(\psi\), gives the opening of the joint in the normal direction per unit of shear displacement for an unconfined joint.

In real rocks, dilation is usually limited by large accumulated shear displacements. It is therefore advisable to specify a critical shear displacement, \(u_{cs}\), above which there will be no dilation.

The dilation is actually applied as a normal force rather than a displacement. Therefore, for a joint with compressive normal stress acting on it, the opening will be less than the \(\tan\psi\) times the shear displacement. The applied force is given by:

(3)\[ \begin{align}\begin{aligned}\Delta \sigma_n = k_n \Delta u_s \tan\psi \; , \; u_s < u_{cs}\\\Delta \sigma_n = 0 \; , \; u_s > u_{cs}\end{aligned}\end{align} \]

where \(k_n\) is the normal stiffness, \(u_s\) is the plastic shear displacement and \(u_{cs}\) is the critical plastic shear displacement. The default value for \(u_{cs}\) is infinity (no dilation limit).

See Figure 4 for typical dilation behavior on an unconfined joint.

Figure 4: 3DEC Joint dilation behavior on an unconfined joint for the Mohr-Coulomb joint model.

States

Each subcontact has a failure state associated with it. The failure state can be plotted (Joint Subcontact plot item) and queried with FISH (block.subcontact.state). When querying with FISH, the state is represented by a variable with 64 bits. Each bit refers to a potential state. The potential states for the Mohr-Coulomb model are shown in the table below.

MC Failure States	Value	Label
Failure in shear now	1	slip-n
Failure in tension now	2	tension-n
Failure in shear in the past	4	slip-p
Failure in tension in the past	8	tension-p

Combinations of states are possible by turning on different bits. For example, a subcontact that failed in tension in the past and is shearing now would have a state value of 8 + 1 = 9. A value of 0 indicates no failure (elastic).

Summary of Mohr-Coulomb Parameters

The model parameters associated with the mohr-coulomb model are summarized in Table 2. The model is accessed in 3DEC with the block contact jmodel assign mohr command.

Table 2: Parameters associated with the Mohr-Coulomb joint model

Parameter	Description	Keyword
\(k_n\)	joint normal stiffness (STRESS/LENGTH)	stiffness-normal
\(k_s\)	joint shear stiffness (STRESS/LENGTH)	stiffness-shear
\(\phi\)	friction angle (DEGREES)	friction
\(\phi_{res}\)	residual friction angle (DEGREES). Defaults to phi.	friction-residual
\(c\)	cohesion (STRESS)	cohesion
\(c_{res}\)	residual cohesion (STRESS). Defaults to 0.	cohesion-residual
\(\psi\)	dilation angle (DEGREES)	dilation
\(u_{cs}\)	shear displacement at which dilation stops (LENGTH). Default is infinity	dilation-zero
\(T_f\)	tensile strength (STRESS)	tension
\(T_f^{res}\)	residual tensile strength (STRESS). Default is 0.	tension-residual

Example

The following example illustrates the behavior with a simple test model. The problem application is the analysis of joint slip around an underground excavation. A simple model is created to evaluate the adequacy of the Mohr-Coulomb slip model to represent the response of a joint subjected to shear loading.

To view this example in 3DEC, use the menu command Help -> Examples…. Choose “3DEC/ Constitutive_Models/ JMohr” and select “slip.prj” to load. The data file used is shown at the end of this example.

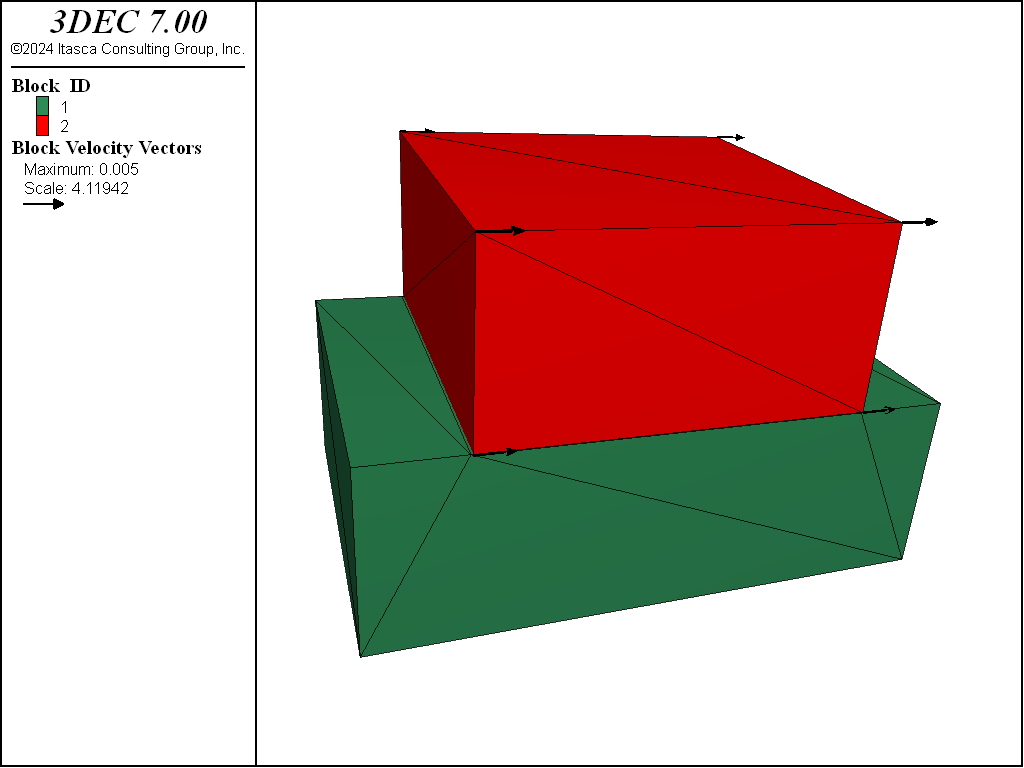
The test is a simulation of a direct shear test, which consists of a single horizontal joint that is first subjected to a normal confining stress, and then to a unidirectional shear displacement. Figure 5 shows the model; the joint is defined by one contact that is composed of 10 sub-contacts.

Figure 5: 3DEC joint dilation behavior on an unconfined joint for the Mohr-Coulomb joint model.

First, a normal stress of 20 MPa — which is representative of the confining stress acting on the joint — is applied. A horizontal velocity is then applied to the top block to produce a shear displacement that is also representative of the displacements expected in the problem application. For demonstration purposes, we only apply a small shear displacement of less than 1 mm to this model.

The average normal and shear stresses, and normal and shear displacements along the joint, are measured with a FISH function (sstav). With this information we can determine the peak and residual shear strengths and dilation that are produced with the different models. The data file for this test using the Mohr-Coulomb slip model is shown in Example Data File.

The average shear stress versus shear displacement along the joint is plotted in Figure 6, and the average normal displacement versus shear displacement is plotted in Figure 7. These plots indicate that joint slip occurs for the prescribed model properties and conditions. The loading slope in Figure 6 is linear until a peak shear strength of approximately 2.9 MPa is reached. As indicated in Figure 7, the joint begins to dilate when the joint fails in shear, at roughly 0.3 mm shear displacement. Dilation occurs until the limiting shear displacement (dilation-zero = 0.6 mm) is reached for zero dilation. The maximum average dilation is approximately 0.077 mm.

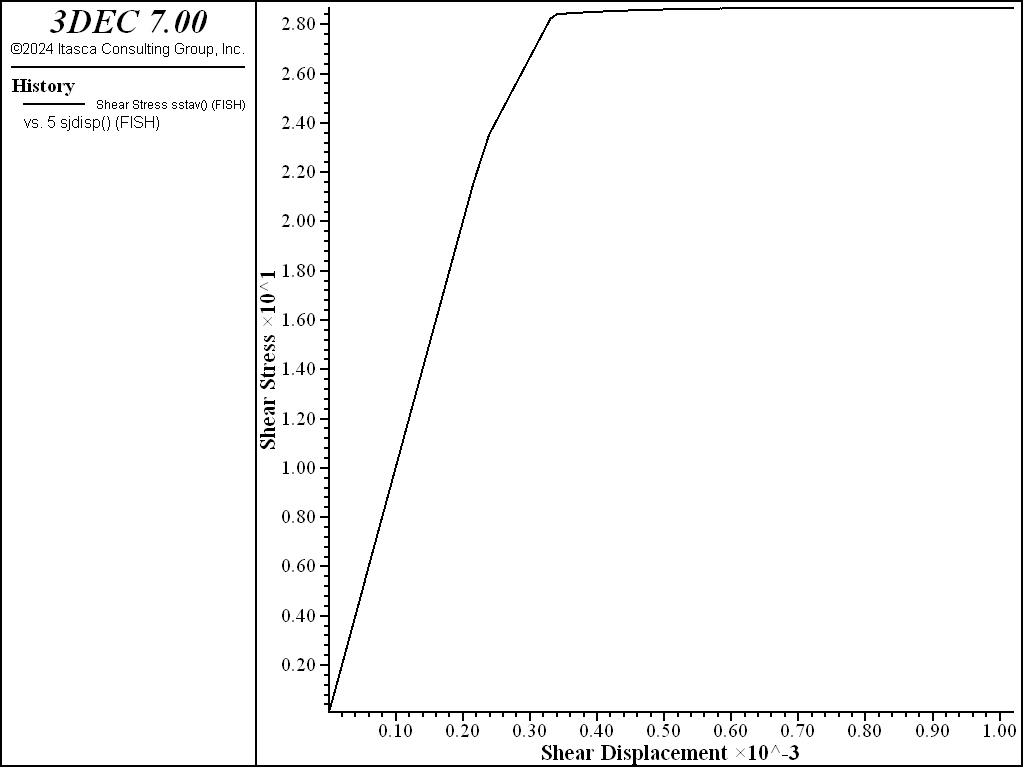
Figure 6: Average shear stress versus shear displacement in the Mohr-Coulomb joint model with cohesion = 0.

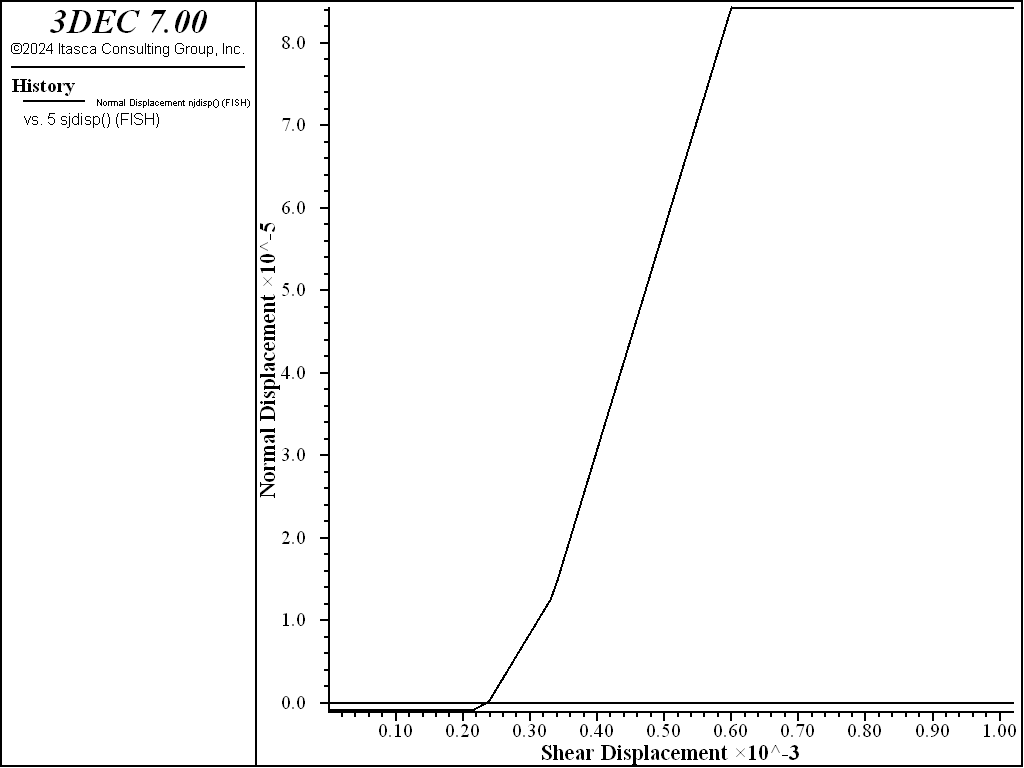
Figure 7: Average normal displacement versus shear displacement in the Mohr-Coulomb joint model with cohesion = 0.

As these results indicate, the Mohr-Coulomb slip model with zero cohesion only defines a limiting shear strength value for the joint. The dilation that occurs after the joint begins to slip is approximated as a linear function of the dilation angle, with a dilation limit that is a function of the shear displacement.

A displacement-weakening behavior can be approximated by including a joint cohesion of 10 MPa (block contact property cohesion = 10). At the onset of failure, the cohesion is set to zero. The results shown in Figure 8 illustrate the peak and residual strengths that develop when the effect of cohesion is included. Note that the drop in strength occurs abruptly. The maximum dilation (as shown in Figure 9) is lower than the previous case without cohesion for the same limiting shear displacement, because more shear displacement occurs before the joint fails initially. (Compare Figure 9 to Figure 7.)

Note that if no weakening behavior is associated with a joint that has a cohesive strength, the residual cohesion (cohesion-residual) should be set equal to the peak cohesion (cohesion). In this case, there will be no change in the cohesion when the joint fails.

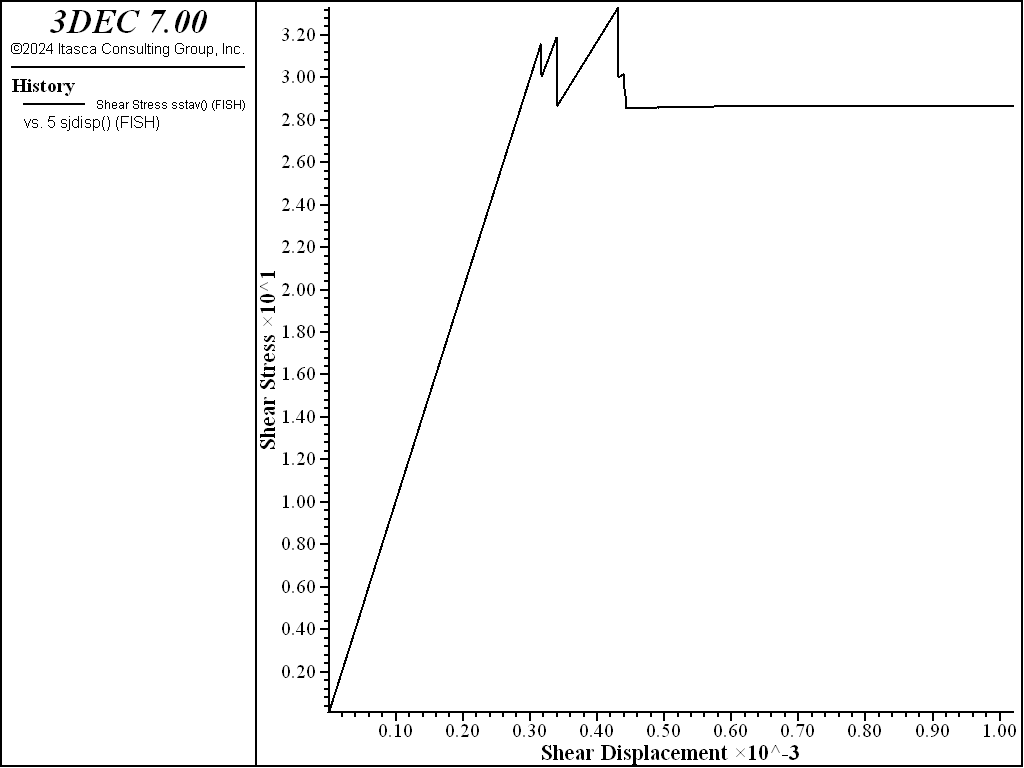
Figure 8: Average shear stress versus shear displacement in the Mohr-Coulomb joint model with cohesion = 10 MPa.

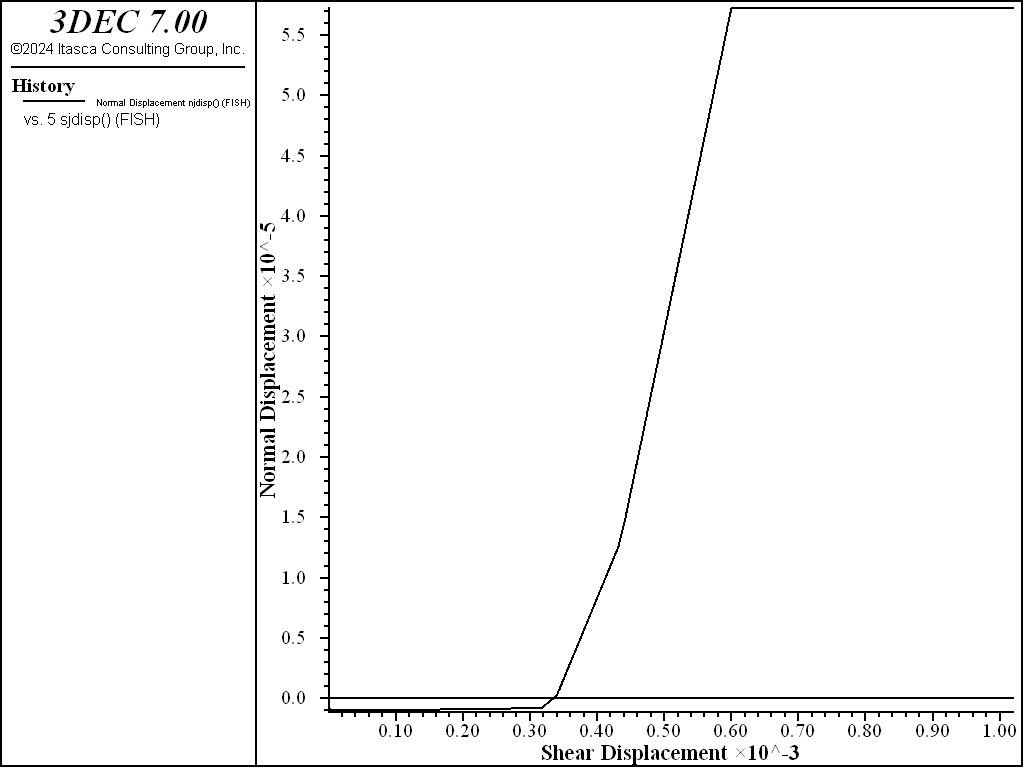
Figure 9: Average normal displacement versus shear displacement in the Mohr-Coulomb joint model with cohesion = 10 MPa.

Data File

slip.dat

model new
model large-strain on

;   Coulomb slip joint model
;   direct shear test
;
block create brick  -0.15,0.15 -0.10,0.10 -0.10,0
block create brick  -0.10,0.10  -0.10,0.10 0,0.10

block zone generate edgelength  0.2

block zone cmodel assign elastic
block zone prop  dens=0.0026  bulk=4000   shear=3000
;
 ;  Coulomb slip model
block contact jmodel assign mohr
block contact prop stiffness-normal=100000 stiffness-shear=100000  ...
                   friction=30.0 dilation 15 dilation-zero 6e-4

;; Use cohesion for weakening behavior
;block contact prop cohesion 10

block contact material-table default prop stiffness-normal=100000  ...
                                          stiffness-shear=100000  ...
                                          friction=30.0 dilation 15 ...
                                          dilation-zero 6e-4

block hide range pos-z 0 1
block gridpoint apply vel 0 0 0 range pos-z -1 0.1
block hide off
;
; normal load
block face apply stress 0 0 -50  0 0 0 range pos-z 0.1
;
model cycle 100
;
;  function to calculate average joint stresses
;  and average joint displacements
;
fish def sstav
   local sstav_vec = vector(0,0,0)
   nstav = 0.0
   njdisp = 0.0
   local sjdisp_vec = vector(0,0,0)
   local jarea = 0.0
   loop foreach cx block.subcontact.list
         ; weight by area
         local area_ = block.subcontact.area(cx)
         sstav_vec = sstav_vec + block.subcontact.force.shear(cx)
         nstav = nstav + block.subcontact.force.norm(cx)
         njdisp = njdisp + block.subcontact.disp.norm(cx)*area_
         sjdisp_vec = sjdisp_vec + block.subcontact.disp.shear(cx)*area_
         jarea = jarea + area_
      endloop
    if jarea > 0
        sstav = math.mag(sstav_vec) / jarea 
        nstav = nstav / jarea 
        njdisp = njdisp / jarea
        sjdisp = math.mag(sjdisp_vec) / jarea
    endif
end
;
block contact reset disp

; shear load
block hide range pos-z -.1 0.0
block gridpoint apply  vel-x=0.005 range pos-z -.1 1.1
block gridpoint apply  vel-y 0 range pos-z -1 1
block hide off
;
his interval 5
model hist  mechanical unbal-max
fish hist name 'Shear Stress' sstav
fish hist name 'Normal Stress' nstav
fish hist name 'Normal Displacement'  njdisp
fish hist name 'Shear Displacement' sjdisp
;
block contact hist  disp-shear pos -1 -1 0
block contact hist disp-norm pos -1 -1 0
block contact hist  disp-shear pos -1  1 0
block contact hist disp-norm pos -1  1 0
block contact hist  disp-shear  pos 0  0 0
block contact hist disp-norm  pos 0  0 0
block contact hist  stress-shear pos -1 -1 0
block contact hist stress-norm pos -1 -1 0
block contact hist  stress-shear pos -1  1 0
block contact hist stress-norm pos -1  1 0
block contact hist  stress-shear pos  0  0 0
block contact hist stress-norm pos  0  0 0
block contact hist  force-shear pos -1 -1 0
block contact hist force-norm pos -1 -1 0
model cyc 15000

model save 'slip1'
program return

Properties

mohr

cohesion f

Joint cohesion.

cohesion-residual f

Residual joint cohesion.

dilation f

Joint dilation angle in degrees.

dilation-zero f

Shear displacement at which joint will cease to dilate.

friction f

Friction angle in degrees.

friction-residual f

Residual joint friction angle in degrees.

stiffness-normal f

Joint normal stiffness (stress / distance)

stiffness-shear f

Joint shear stiffness (stress / distance)

tension f

Tensile strength.

tension-residual f

Residual joint tensile strength.