Uniaxial Compressive Strength of a Jointed Material Sample (FLAC2D)

Problem Statement

Note

The project file for this example is available to be viewed/run in FLAC2D.[1] The main data files used are shown at the end of this example.

The uniaxial compressive strength of a material is evaluated numerically using the ubiquitous-joint model. This model takes into consideration a direction of weakness (ubiquitous-joint) in a Mohr-Coulomb material on which shear failure can be initiated. The compressive strength of the sample is a function of the material and joint properties, as well as the angle, \(\beta\), formed by the direction of the compressive stress and its projection onto the plane of weakness (see Figure 1).

In this example, the sample is selected as a an infinite block and plane strain conditions are used. The width of the block is \(a\), and height, \(b\), such that \(b/a\) = 2. The Mohr-Coulomb material has the following properties.

shear modulus (\(G\))

70 MPa

bulk modulus (\(K\))

100 MPa

cohesion (\(c\))

2 kPa

friction angle (\(\phi\))

40°

dilation angle (\(\psi\))

0°

tension limit (\(\sigma^t\))

2.4 kPa

The ubiquitous-joint properties include the following.

cohesion (\(c_j\))

2 kPa

friction angle (\(\phi_j\))

30°

dilation angle (\(\psi_j\))

0°

tension limit (\(\sigma_j^t\))

2.4 kPa
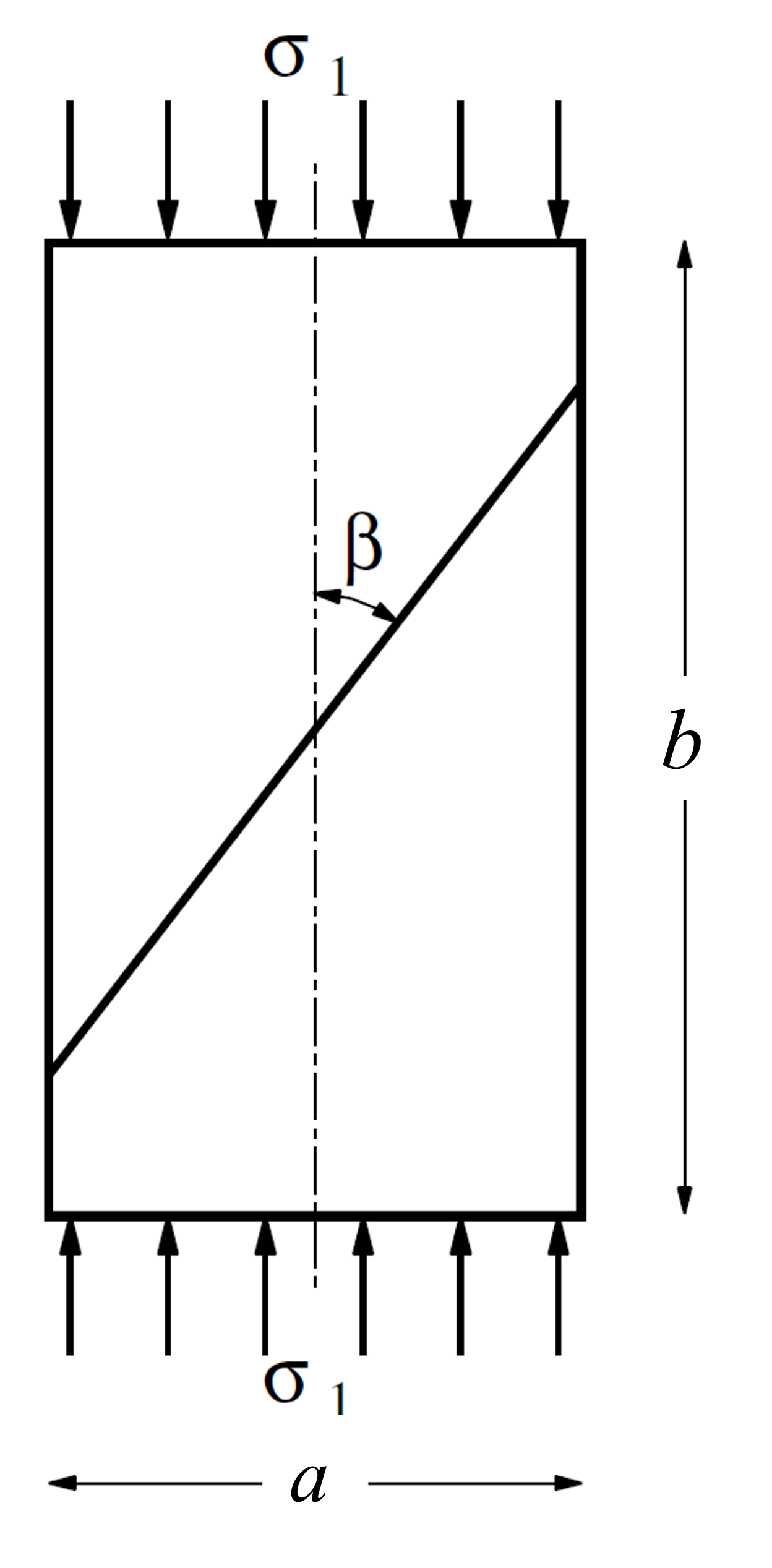
../../../../../_images/jointed-geom-2d.png

Figure 1: Problem geometry.

Analytical Prediction

As a definition, let

\[\kappa = 1 - \tan(\phi_j) \tan(\beta)\]

in which \(\beta\) is the weak-plane angle, as indicated in Figure 1. Before failure occurs, the state of stress is homogeneous in the sample. Failure will be initiated on the weak plane when, for \(\kappa >\) 0,

\[-\sigma_1 = {{2 c_j}\over{\kappa \sin 2\beta}}\]

provided the value \(-\sigma_1\) of the compressive strength (tension positive) does not violate the Mohr-Coulomb failure criterion,

\[-\sigma_1 = 2 c \sqrt N_{\phi}\]

in which

\[N_{\phi} = {{1 + \sin\phi}\over{1 - \sin\phi}}\]

If this criterion is violated, or if \(\kappa \leq\) 0, failure will occur in the matrix instead, on planes inclined at an angle of \((\pi/4 - \phi/2)\) with respect to the axis of symmetry of the sample. See Jaeger and Cook (1979) for details.

FLAC2D Model

For the numerical simulation, a block with a width of 2 m and height of 4 m is selected. The domain is discretized into 8 quadrilateral zones as shown Figure 2. A uniform velocity is applied in the \(y\)-direction at both ends of the block to induce compression of the sample.

The effect of the variation of \(\beta\) has been studied every five degrees from 0° to 90°. The input file uses a FISH function (solveAll) to calculate the compressive strength at each \(\beta\) value. A zone delete command is issued prior to each calculation at a different \(\beta\). This deletes all zones to effectively reset the model. The final vertical stress calculated with FISH function sigmav is added to a table at the end of each run. This approach saves the whole parametric analysis in one file.

After initiation of the failure mechanism, the state of stress in the sample becomes nonuniform. To better control the deformation of the system, the magnitude of the velocities at the top and bottom of the sample are monitored and adapted as a function of the unbalanced force value (servo-control). The servo keyword used in the zone face apply command controls the magnitude of the applied velocity. Cycling continues until an accumulated displacement of 4.5e-4 is reached (using the FISH function halt), indicating enough total strain to cause failure at all angles.

../../../../../_images/jointed-grid-2d.png

Figure 2: FLAC2D grid—uniaxial compressive strength test.

Results and Discussion

Figure 3 compares results of the FLAC2D runs with the analytical compressive strength predictions. The match is very good, with a relative error smaller than 1% for all values of \(\beta\).

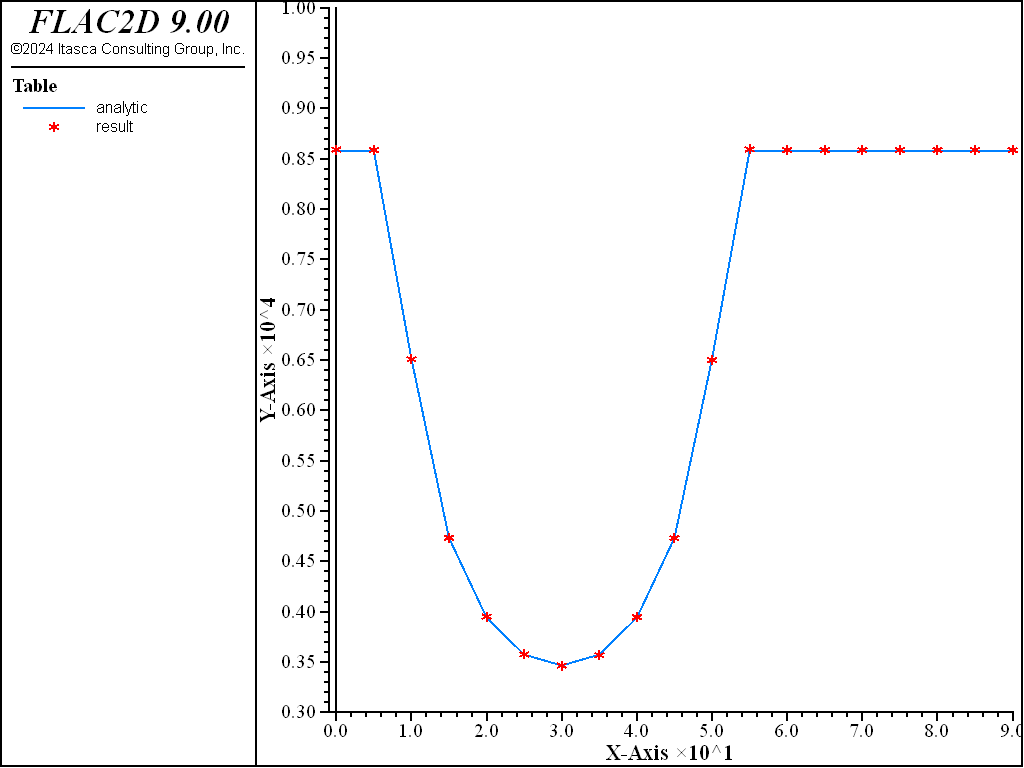
../../../../../_images/jointed-strength-2d.png

Figure 3: Compressive strength comparison.

Reference

Jaeger, J. C., and N. G. W. Cook. Fundamentals of Rock Mechanics, 3rd Ed. New York: Chapman and Hall (1979).

Data Files

UniaxialStrengthJointed.dat

;---------------------------------------------------------------------
; compression test of cylindrical sample using
;   ubiquitous joint model
;---------------------------------------------------------------------
model new
model large-strain off
fish automatic-create off
; Create the Sketch data, generated interactively
; and exported from the State Record
program call 'geometry' ; Includes 'top' and 'bottom' group assignments
; Load FISH functions used to support - 
; the strength calculation and the halt function
program call 'fish-support'
; The main function that 
fish define solveAll
    loop local beta (0,90,5) ; Check angles from 0 to 90 in 5 degree increments
        command
            zone delete ; Remove all existing zones
            zone generate from-sketch ; Generate new zones from Sketch
            zone cmodel assign ubiquitous-joint ; Assign model and properties
            zone property bulk 1e8 shear 7e7 cohesion 2e3 friction 40 ...
                          dilation 0 tension 2400 angle [90-beta] ...
                          joint-cohesion 1e3 joint-friction 30 ...
                          joint-dilation 0 joint-tension 2400
            ; Assign boundary conditions
            zone gridpoint free velocity
            zone face apply velocity-normal -5e-8 servo ... 
                    ratio local minimum 1e-4 range group 'Top' or 'Bottom'
            ; Cycle till the target strain is reached
            model solve fish-halt [halt]
            ; Add results to table
            table 'result' add ([beta],[sigmav])
        end_command
    end_loop
end
; Run all 18 cases
[solveAll]
; Save the last state, and the accumulated table
model save 'final'

fish-support.dat

; Function that calculates final strength
fish define sigmav
    local gps = gp.list( gp.isgroup(::gp.list,'bottom') )
    return -list.sum(gp.force.unbal(::gps)->y) / 2
end

; Function that determines if solving should stop
fish define halt
    global gpHalt = gp.near(0,0)
    halt = gp.disp.y(gpHalt ) > 4.5e-4
end

Endnote