Using FISH Callbacks
Introduction
Note
The project file for this example may be viewed/run in PFC.[1] The data files used are shown at the end of this example.
The fish callback command can be used to register user-defined FISH functions to be executed in response to specific callback events during a simulation. Callbacks can occur:
at select positions in the cycle sequence; or
in response to specific events.
This tutorial illustrates several situations where one can use callbacks to execute FISH functions.
Numerical Model
To reproduce the models discussed below, open the project file named “Callbacks.prj” available under the menu of PFC3D.
Position in the Calculation Cycle
The calculation cycle consists of a series of operations that are executed in a specific order. Each operation is associated with a floating point number milestone, also referred to as a cycle point (see below).
Cycle Point |
Cycle Operation |
|---|---|
-10.0 |
|
0.0 |
|
10.0 |
|
15.0 |
|
20.0 |
|
30.0 |
|
35.0 |
|
40.0 |
|
42.0 |
|
45.0 |
|
60.0 |
Second pass of equations of motion (not used in PFC) |
70.0 |
Thermal calculations (not used in PFC) |
80.0 |
Fluid calculations (not used in PFC) |
Interfering with calculations as they occur could be dangerous and is not permitted. For instance, if one was able to delete a ball while the timestep was being calculated on that ball, the code would crash. As a result, the cycle points are reserved, in that the user is not allowed to attach a FISH function to a callback event at those cycle points. For similar reasons, the user is not allowed to interfere between cycle points 40.0 (force-displacement calculations) and 42.0 (accumulation of deterministic quantities), and the creation and deletion of model components (balls, clumps, or pebbles and walls or facets) is only permitted before cycle point 0.0 (timestep evaluation).
Except for these limitations, the user may register FISH functions to be executed into the cycle sequence to operate on the model by registering those functions at user-defined cycle points (e.g., cycle points 10.1, 10.15, 10.3, etc.).
Creating Balls
The first example demonstrates the periodic insertion of balls into a model. The complete data file for this example is “callbacks1.dat (3D)”. Select lines are discussed below.
A simple system consisting of balls interacting in a box is modeled. Balls are created at a given frequency using the FISH function add_ball.
fish define add_ball
global tnext,freq
local tcurrent = mech.time.total
if tcurrent < tnext then
exit
endif
tnext = tcurrent + freq
local xvel = (math.random.uniform -0.5) * 2.0
local yvel = (math.random.uniform -0.5) * 2.0
local bp = ball.create(0.3,vector(0.0,0.0,1.75))
ball.vel(bp) = vector(xvel,yvel,-2.0)
ball.density(bp) = 1.1e3
ball.damp(bp) = 0.1
end
This function is registered (see the fish callback command) at the cycle point -11.0 before the data structures are validated. As add_ball is executed during each cycle, the current mechanical age is checked against the next insertion time to decide whether or not to create a ball.
[freq = 0.25]
[time_start = mech.time.total]
[tnext = time_start ]
fish callback add add_ball -11.0
The model is cycled for a given target time with the command below.
model solve time 10.0
While cycles are performed, balls are inserted in the model (Figure 1). Note that balls continue to be inserted in the model with additional cycling as the add_ball function remains registered at cycle point -11.0.
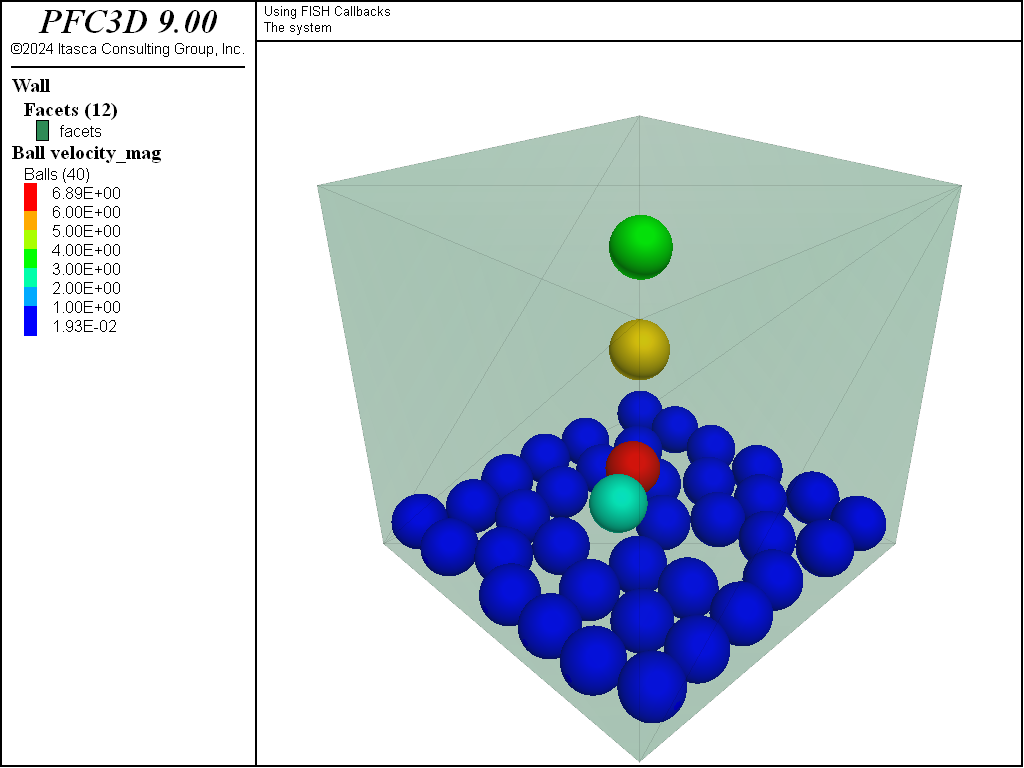
Figure 1: The system during cycling with the add_ball FISH function registered as a callback.
In this example, the add_ball function is removed from the callback list and the model is solved to equilibrium. Thus, no additional balls are inserted and the model reaches an equilibrium state (shown in Figure 2).
fish callback remove add_ball -11.0
model solve
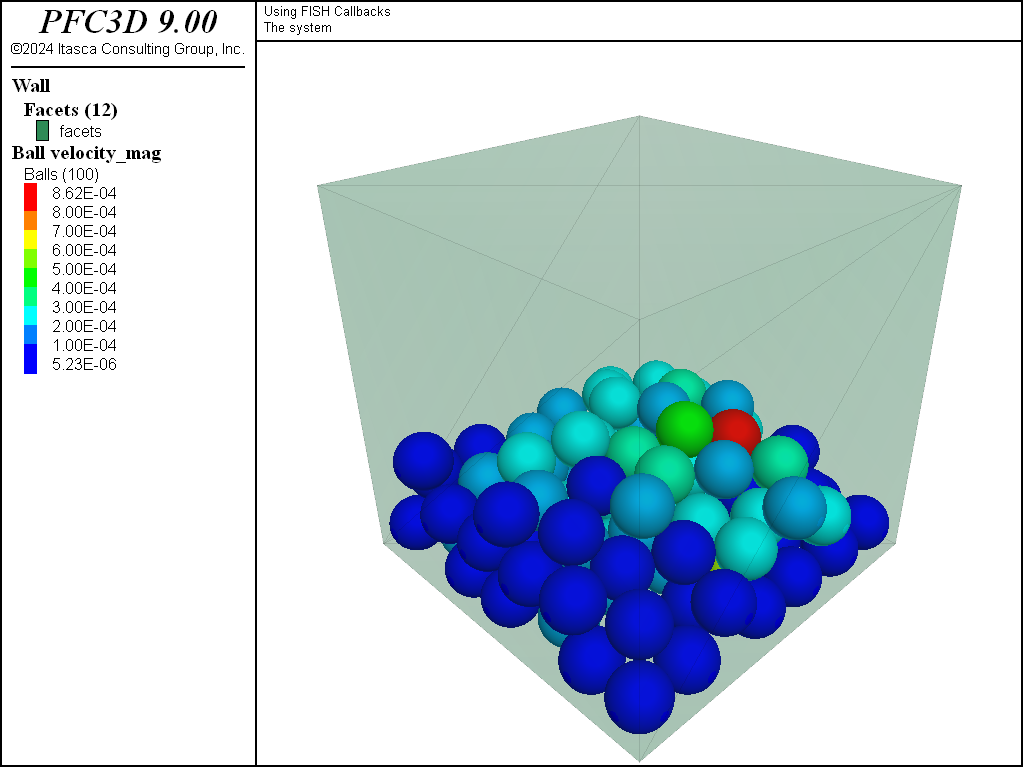
Figure 2: Final state of the system.
Incorporating New Physics
The second example (”callbacks2.dat (3D)”) builds upon the example above. Two additional FISH functions, registered at different points in the cycle sequence, are introduced. These functions apply additional forces to the balls, modeling the effect of a fluid in the box.
First, a function named add_fluidforces is defined:
fish define add_fluidforces
global vf = 0.0
global zf_, etaf_, rhof_
loop foreach ball ball.list
local vi = 0.0
local d1 = ball.pos.z(ball) - ball.radius(ball)
if ball.pos.z(ball) - ball.radius(ball) >= zf_
; above water level
ball.force.app(ball) = vector(0.0,0.0,0.0)
else
local fdrag = -6.0*math.pi*etaf_*ball.radius(ball)*ball.vel(ball)
local vbal = 4.0*math.pi*ball.radius(ball)^3 / 3.0
if ball.pos.z(ball) + ball.radius(ball) <= zf_ then
; totally immerged
vi = 4.0*math.pi*ball.radius(ball)^3 / 3.0
else
; partially immerged
if ball.pos.z(ball) >= zf_ then
global h = ball.radius(ball) - (ball.pos.z(ball)-zf_)
global vcap = math.pi*h^2*(3*ball.radius(ball) - h) /3.0
vi = vcap
else
h = ball.radius(ball) - (zf_ - ball.pos.z(ball))
vcap = math.pi*h^2*(3*ball.radius(ball) - h) /3.0
vi = vbal - vcap
endif
endif
global fb = -1.0*rhof_*vi*global.gravity
ball.force.app(ball) = fb + (vi/vbal) *fdrag
endif
vf = vf + vi
endloop
end
This function loops over all the balls in the system using the ball.force.app FISH intrinsic to apply additional forces. The applied force is a combination of a buoyancy term, \(\mathbf{F_b}\), and a drag term, \(\mathbf{F_d}\), computed as
where \(\rho_f\) is the fluid density, \(V_i\) is the immersed ball volume, \(\mathbf{g}\) is the gravity vector, \(\eta_f\) is the fluid dynamic viscosity, \(R\) is the ball radius, \(\alpha\) is the ratio of non-immersed ball volume to the total ball volume and \(\mathbf{v}\) is the ball velocity vector. The expression chosen for \(\mathbf{F_d}\) is typical for a single sphere completely immersed in a fluid in the laminar regime (e.g., large fluid viscosity). The factor \(\alpha\) is introduced to scale down the drag force when the ball is only partially immersed.
A second function, named move_surface, is also implemented:
fish define move_surface
global zf0_, gset_
zf_ = zf0_ + (vf/16.0)
loop foreach node geom.node.list(gset_)
geom.node.pos.z(node) = zf_
endloop
end
The purpose of this function is to adjust the fluid surface height, zf_, according to the sum of the immersed volume of balls accumulated by add_fluidforces. In turn, the modified value of zf_ is used in add_fluidforces to adjust buoyancy during the next cycle. The function move_surface also modifies the height of the nodes of a geometry object added to the model to visualize the fluid surface:
[rhof_ = 1.26e3]
[zf0_ = -1.0]
[zf_ = zf0_]
[etaf_ = 1.49]
geometry set 'surface' polygon create by-positions -2.0 -2.0 [zf0_] ...
2.0 -2.0 [zf0_] ...
2.0 2.0 [zf0_] ...
-2.0 2.0 [zf0_]
[gset_ = geom.set.find('surface')]
The parameters are chosen to simulate a fluid with viscosity larger than the ball density.
Before cycles are executed, the two functions discussed above are registered as callbacks in the cycle sequence at cycle points with values 50.0 and 50.1:
fish callback add add_fluidforces 50.0
fish callback add move_surface 50.1
This ensures that both functions are executed after all built-in operations in the PFC cycle sequence and that move_surface is executed after the total non-immersed volume has been updated. Should additional computation be required between the two functions, an additional FISH function could be registered (with a cycle point with value 50.05, for instance).
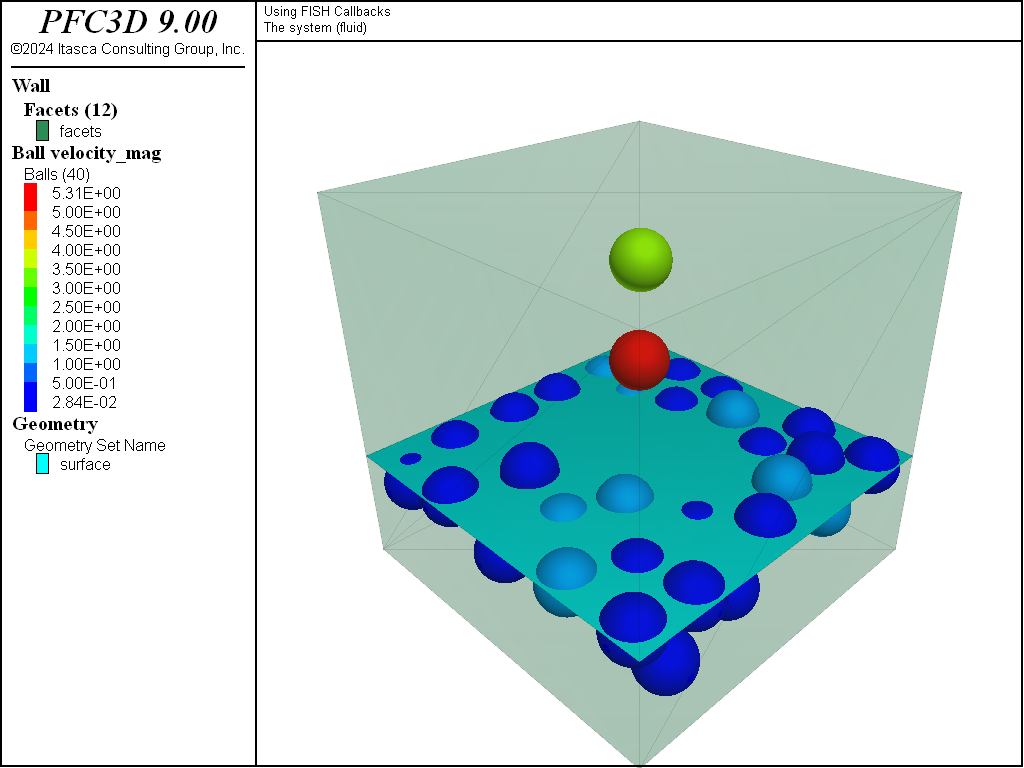
Figure 3: Intermediate state of the system with fluid force active.
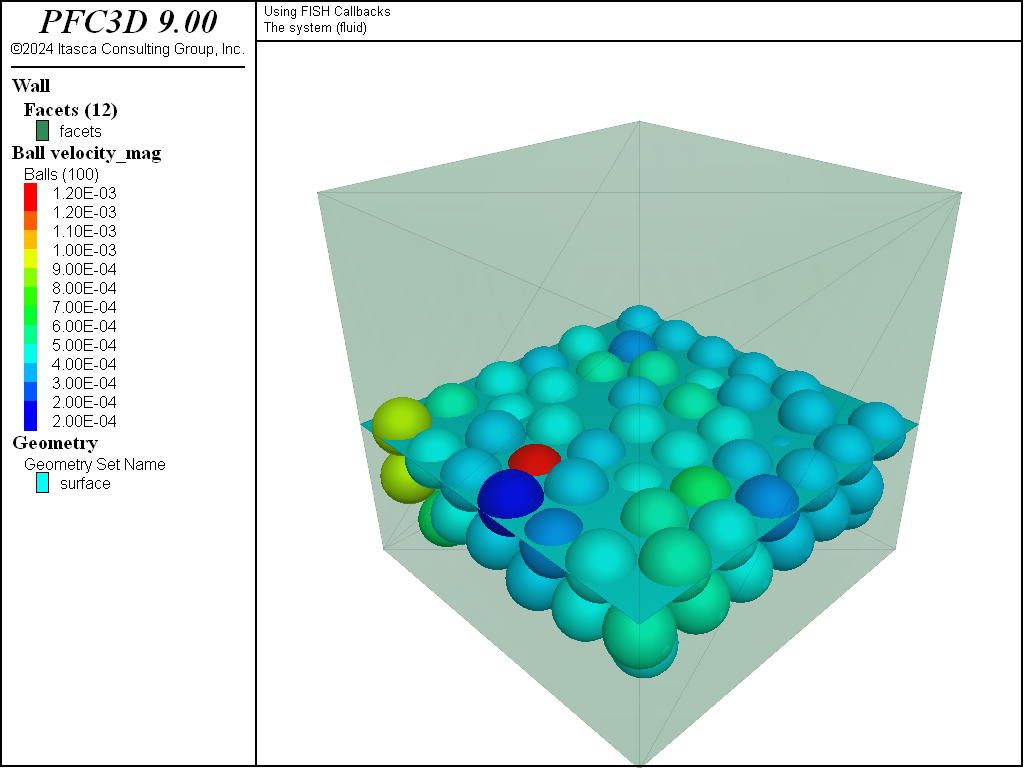
Figure 4: Final state of the system with fluid force active.
Figures 3 and 4 show the state of the system during cycling and in its final stable configuration, respectively. Balls are added periodically, and the balls are pushed toward the fluid surface due to the buoyancy force, with motion damped by the fluid drag force.
The model described here may seem oversimplified. Notably, the expression of the drag force does not account for fluid velocity. However, this simple example demonstrates how new physics can be added to PFC with just a few steps. Should a more sophisticated model including fluid-mechanical coupling be required, more elaborate algorithms could be devised, or coupling with a third party CFD solver could be envisioned (see the section “CFD module for PFC3D”).
Named Callback Events
To provide more flexibility, one may also register FISH functions to be executed in response to named events that may occur during the cycle sequence. A list of events is shown in below. This list may not be exhaustive because new events can be added by user-defined contact models.
Event Type |
Event Name |
Argument(s) |
|---|---|---|
contact model |
contact_activated |
FISH array, contact model-specific |
contact model |
slip_change |
FISH array, contact model-specific |
contact model |
bond_break |
FISH array, contact model-specific |
contact model |
bond_broken |
FISH array, contact model-specific |
create/delete |
contact_create |
contact pointer |
create/delete |
contact_delete |
contact pointer |
create/delete |
ball_create |
ball pointer |
create/delete |
ball_delete |
ball pointer |
create/delete |
clump_create |
clump pointer |
create/delete |
clump_delete |
clump pointer |
create/delete |
rblock_create |
rblock pointer |
create/delete |
rblock_delete |
rblock pointer |
create/delete |
facet_create |
wall facet pointer |
create/delete |
facet_delete |
wall facet pointer |
create/delete |
wall_create |
wall pointer |
create/delete |
wall_delete |
wall pointer |
create/delete |
ballthermal_create |
ballthermal pointer |
create/delete |
ballthermal_delete |
ballthermal pointer |
create/delete |
clumpthermal_create |
clumpthermal pointer |
create/delete |
clumpthermal_delete |
clumpthermal pointer |
create/delete |
wallthermal_create |
wallthermal pointer |
create/delete |
wallthermal_delete |
wallthermal pointer |
create/delete |
ballcfd_create |
ballcfd pointer |
create/delete |
ballcfd_delete |
ballcfd pointer |
create/delete |
clumpcfd_create |
clumpcfd pointer |
create/delete |
clumpcfd_delete |
clumpcfd pointer |
solve |
cfd_before_send |
|
solve |
cfd_after_received |
|
solve |
cfd_before_update |
|
solve |
cfd_after_update |
|
solve |
solve_complete |
An important feature of named callback events is that arguments may be passed to the associated FISH function when it is executed. For instance, if the contact_create event is triggered, then a pointer to the new contact is passed as an argument to the registered FISH functions if they accept arguments. Contact model events always pass FISH arrays as arguments, with the content of the array depending on the implementation of the contact model.
The last example in this tutorial (see “callbacks3.dat (3D)”) illustrates how the contact_create and contact_activated events can be used. The model starts with the final configuration obtained with “callbacks1.dat (3D)” (i.e., balls settled under gravity in a box). In this case, the orientation of gravity is modified to be parallel with the \(x\)-direction, causing balls to flow toward the corresponding side of the box. A FISH function is registered with either the contact_create or the contact_activated event, whose purpose is to query whether the contact is between a ball and the top side of the box. In this circumstance, the ball is deleted. In this way, the top of the box is acting as a particle sink. Since these two events do not return the same list of arguments, the functions must differ slightly (as discussed below).
Contact Creation Event
The FISH function below can be registered with the contact_create event:
fish define catch_contacts(cp)
if type.pointer(cp) # 'ball-facet' then
exit
endif
wfp = contact.end2(cp)
if wall.id(wall.facet.wall(wfp)) # 2 then
exit
endif
map.add(todelete,ball.id(contact.end1(cp)),contact.end1(cp))
end
fish callback add catch_contacts event contact_create
In this case, a contact pointer is passed as an argument to catch_contacts. Note that this event is triggered whenever any contact is created in the system (i.e., including ball-ball contacts). Therefore catch_contacts must check whether the contact occurs between a ball and a wall facet, before checking the ID of the wall. If the contact is a ball-facet contact and it is with a facet of the top wall (i.e., wall ID 2), the ball is added to a list of balls to be deleted. The ball cannot be deleted automatically because the ball creation/deletion is limited to cycle points prior to 0.
The final state of the system after cycling is shown in Figure 5. Note that contacts in PFC are created at the discretion of the contact detection logic, as discussed in the section “Contacts and Contact Models.” It is guaranteed that a contact between two pieces will be created before the pieces actually interact, meaning that there is no exact control of the distance at which a contact will be created. A drawback of the approach given in this example is that balls that do not overlap the top wall may be deleted.
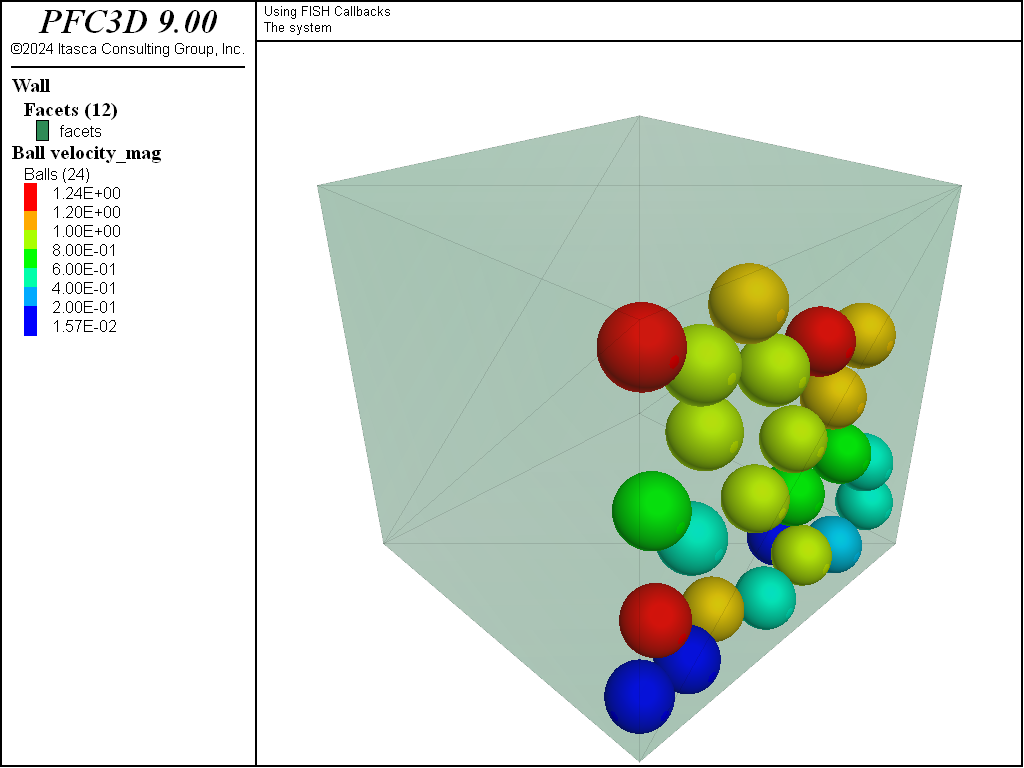
Figure 5: Final state of the system. Gravity is parallel to the x-axis, and balls are deleted as contacts with the top wall are created.
Contact Model Events
An alternative method to overcome ball deletion prior to overlap with a wall facet is to register a FISH function with the contact_activated event defined by the linear contact model:
fish define catch_contacts(arr)
local cp = arr(1)
if type.pointer(cp) # 'ball-facet' then
exit
endif
local wfp = contact.end2(cp)
if wall.id(wall.facet.wall(wfp)) # 2 then
exit
endif
map.add(todelete,ball.id(contact.end1(cp)),contact.end1(cp))
end
fish callback add catch_contacts event contact_activated
Here the argument passed to catch_contacts is a FISH array containing the contact pointer. This corresponds with the linear model implementation. Except for this difference, this version of catch_contacts operates as described above. However, since the contact_activated event of the linear model is triggered when the contact becomes active, the balls are deleted only when they physically overlap a facet of the upper wall. The final state of the system after cycling is shown in Figure 6.
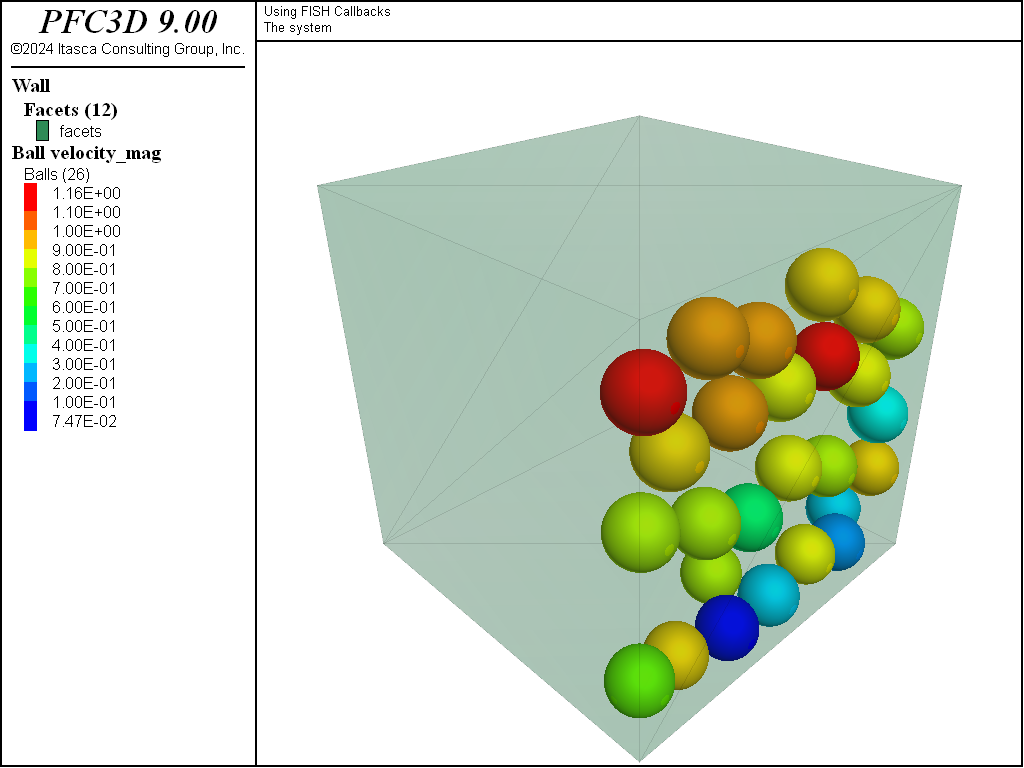
Figure 6: Final state of the system. Gravity is parallel to the x-axis, and balls are deleted when they physically overlap the top wall.
Discussion
This tutorial demonstrates the use of the PFC callback mechanism to execute FISH functions in several situations. FISH functions can be registered to be executed at select points in the cycle sequence or in response to named events. Any user-defined FISH function can be registered as a callback with the fish callback command. There is no need for the function to accept arguments, though they may be useful. The list of potential arguments depends on the specific event.
Data Files
callbacks1.dat (3D)
; fname: callbacks1.dat
;
; Demonstrate usage of the set fish callback command to insert balls at a
; given rate while cycling
;
;=========================================================================
model new
model large-strain on
model random 10001
model title 'Using FISH Callbacks'
; Define the domain and the default contact model
model domain extent -3 3
contact cmat default model linear property kn 1.0e6 dp_nratio 0.5
; Generate a box and set gravity
wall generate box -2 2
model gravity 10.0
; Define the add_ball function, which will be registered as a fish callback
; and will insert balls at a given frequency in the model
fish define add_ball
global tnext,freq
local tcurrent = mech.time.total
if tcurrent < tnext then
exit
endif
tnext = tcurrent + freq
local xvel = (math.random.uniform -0.5) * 2.0
local yvel = (math.random.uniform -0.5) * 2.0
local bp = ball.create(0.3,vector(0.0,0.0,1.75))
ball.vel(bp) = vector(xvel,yvel,-2.0)
ball.density(bp) = 1.1e3
ball.damp(bp) = 0.1
end
; Set parameters and register the function add_ball with a fish callback at
; position -11.0 in the cycle sequence. Model components cannot be inserted
; in the model after the timestep has been evaluated, which corresponds to
; position 0.0 in the cycle sequence
[freq = 0.25]
[time_start = mech.time.total]
[tnext = time_start ]
fish callback add add_ball -11.0
; Solve to a target time of 10.0 time-units
model solve time 10.0
model save 'intermediate'
; Continue cycling to an additional target time of 15.0 time-units
; Note that the fish callback is still active
model solve time 15.0
; Deactivate the fish callback and solve to equilibrium (default limit
; corresponds to an average ratio of 1e-5)
fish callback remove add_ball -11.0
model solve
model save 'settled'
program return
;=========================================================================
; eof: callbacks1.dat
callbacks2.dat (3D)
; fname: callbacks2.dat
;
; Demonstrate usage of the set fish callback command to insert balls at a
; given rate while cycling and add applied forces to the balls
;=========================================================================
model new
model large-strain on
model random 10001
model title 'Using FISH Callbacks'
; Define the domain and the default contact model
model domain extent -3 3
contact cmat default model linear property kn 1.0e6 dp_nratio 0.5
; Generate a box and set gravity
wall generate box -2 2
model gravity 10.0
; Define the add_ball function, which will be registered as a fish callback
; and will insert balls at a given frequency in the model
fish define add_ball
global tnext, freq
local tcurrent = mech.time.total
if tcurrent < tnext then
exit
endif
tnext = tcurrent + freq
local xvel = (math.random.uniform -0.5) * 2.0
local yvel = (math.random.uniform -0.5) * 2.0
local bp = ball.create(0.3,vector(0.0,0.0,1.75))
ball.vel(bp) = vector(xvel,yvel,-2.0)
ball.density(bp) = 1.1e3
ball.damp(bp) = 0.1
end
; Set parameters and register the function add_ball with a fish callback at
; position -11.0 in the cycle sequence. Model components cannot be inserted
; in the model after the timestep has been evaluated, which corresponds to
; position 0.0 in the cycle sequence
[freq = 0.25]
[time_start = mech.time.total]
[tnext = time_start ]
fish callback add add_ball -11.0
; Define the add_fluidforces function, which will be registered as a fish
; callback and will apply fluid forces (buoyancy and drag) to the balls
fish define add_fluidforces
global vf = 0.0
global zf_, etaf_, rhof_
loop foreach ball ball.list
local vi = 0.0
local d1 = ball.pos.z(ball) - ball.radius(ball)
if ball.pos.z(ball) - ball.radius(ball) >= zf_
; above water level
ball.force.app(ball) = vector(0.0,0.0,0.0)
else
local fdrag = -6.0*math.pi*etaf_*ball.radius(ball)*ball.vel(ball)
local vbal = 4.0*math.pi*ball.radius(ball)^3 / 3.0
if ball.pos.z(ball) + ball.radius(ball) <= zf_ then
; totally immerged
vi = 4.0*math.pi*ball.radius(ball)^3 / 3.0
else
; partially immerged
if ball.pos.z(ball) >= zf_ then
global h = ball.radius(ball) - (ball.pos.z(ball)-zf_)
global vcap = math.pi*h^2*(3*ball.radius(ball) - h) /3.0
vi = vcap
else
h = ball.radius(ball) - (zf_ - ball.pos.z(ball))
vcap = math.pi*h^2*(3*ball.radius(ball) - h) /3.0
vi = vbal - vcap
endif
endif
global fb = -1.0*rhof_*vi*global.gravity
ball.force.app(ball) = fb + (vi/vbal) *fdrag
endif
vf = vf + vi
endloop
end
; Define the move_surface function, which will be registered as a fish
; callback and will update the fluid surface position to account for
; immersed balls volume
fish define move_surface
global zf0_, gset_
zf_ = zf0_ + (vf/16.0)
loop foreach node geom.node.list(gset_)
geom.node.pos.z(node) = zf_
endloop
end
; Set parameters and create a polygon with the geometry logic to
; visualize the fluid surface. Store a pointer to the geometry set
; to be used by the move_surface function.
[rhof_ = 1.26e3]
[zf0_ = -1.0]
[zf_ = zf0_]
[etaf_ = 1.49]
geometry set 'surface' polygon create by-positions -2.0 -2.0 [zf0_] ...
2.0 -2.0 [zf0_] ...
2.0 2.0 [zf0_] ...
-2.0 2.0 [zf0_]
[gset_ = geom.set.find('surface')]
; Register the add_fluidforces and move_surface functions
; at cycle points 50.0 and 50.1 in the cycle sequence respectively.
; The operations will occur after force-displacement calculation, and
; the applied forces will affect the balls at the next step.
; The move_surface function will be called after fluid forces have been
; applied to all the balls (and immersed volumes updated)
fish callback add add_fluidforces 50.0
fish callback add move_surface 50.1
; Solve to a target time of 10.0 time-units
model solve time 10.0
model save 'fluid-intermediate'
; Continue cycling to an additional target time of 15.0 time-units
; Note that the fish callback is still active
model solve time 15.0
; Deactivate the add_ball fish callback and solve to equilibrium
; (default limit corresponds to an average ratio of 1e-5)
fish callback remove add_ball -11.0
model solve
model save 'fluid-final'
program return
;=========================================================================
; eof: callbacks2.dat
callbacks3.dat (3D)
; fname: callbacks3.dat
;
; Demonstrate usage of the set fish callback command to insert balls at a
; given rate while cycling and add fluid forces
;=========================================================================
model restore 'settled'
[todelete = map()]
fish define delete_balls
loop foreach key map.keys(todelete)
local ball = map.remove(todelete,key)
ball.delete(ball)
endloop
end
fish callback add delete_balls -12.0
model gravity 10.0 0.0 0.0
model save 'sink-initial'
; Register a function with the contact_create event
fish define catch_contacts(cp)
if type.pointer(cp) # 'ball-facet' then
exit
endif
wfp = contact.end2(cp)
if wall.id(wall.facet.wall(wfp)) # 2 then
exit
endif
map.add(todelete,ball.id(contact.end1(cp)),contact.end1(cp))
end
fish callback add catch_contacts event contact_create
model solve time 5.0
model save 'sink-final1'
; Register a function with the contact_activated event
model restore 'sink-initial'
fish define catch_contacts(arr)
local cp = arr(1)
if type.pointer(cp) # 'ball-facet' then
exit
endif
local wfp = contact.end2(cp)
if wall.id(wall.facet.wall(wfp)) # 2 then
exit
endif
map.add(todelete,ball.id(contact.end1(cp)),contact.end1(cp))
end
fish callback add catch_contacts event contact_activated
model solve time 5.0
model save 'sink-final2'
program return
;=========================================================================
; eof: callbacks3.dat
Endnote
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Dec 14, 2024 |
