Sliding Wedge

Introduction

Note

The project file for this example may be viewed/run in PFC.[1] The data files used are shown at the end of this example.

In this example, a simple wedge stability analysis is performed. The critical friction angle is calculated using a bisection algorithm written in Python. The result is compared to the analytical solution.

PFC3D Model

The wedge is formed by the intersection of the planar surfaces with a cube. The sliding surfaces of the wedge are defined by:

  • F1: Dip = 40°, dip direction = 130°, Origin=(0,0,1)

  • F2: Dip = 60°, dip direction = 220°, Origin=(0,-0.25,1)

A rigid block defining the model “box” is first created. Then fractures are introduced using the command fracture create. Fractures are finite and have a disk shape. To guarantee their persistence within the model box, a large size is used, for instance 5m. The existing cubic block is then cut by these fractures using the command rblock cut.

The commands to create the model geometry are:

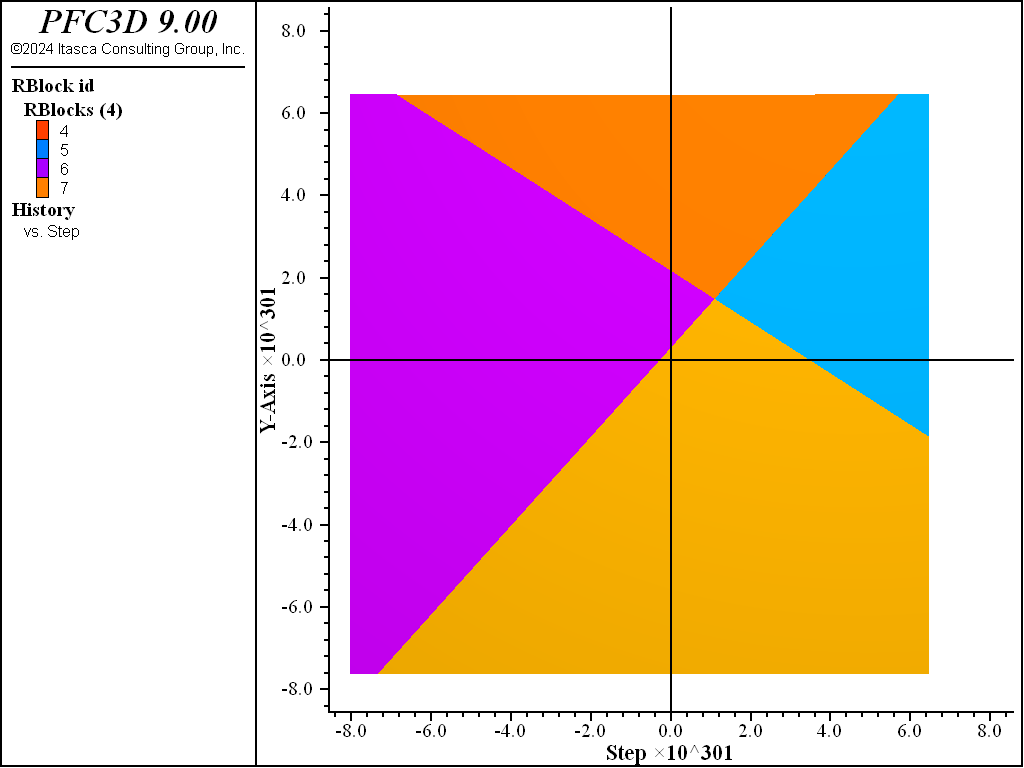
../../../../../../../../_images/p3d-rblocks-sliding-wedge-ini.png

Figure 1: The initial system.

Boundary conditions consist of fixing all blocks except the wedge (block with position nearest (0.0477973,-0.786686,0.82332)). The corresponding commands are:

A unique set of mechanical properties is applied to all contacts: zero cohesion, normal and shear stiffness = 1e7Pa/m, friction coefficient initially very large. The blocks have a density of 2000kg/m3 with a damping equal to 0.7 and are subjected to gravity. The corresponding commands are:

Friction angle will be modified during the analysis in order to calculate the critical friction angle, for which the wedge is at limit equilibrium. Initially, the model is run to initial equilibrium with very large friction.

Analytical Solution

Analytical solution is deduced from [GoodmanShi1985].

For the case of a block sliding on two faces, we define \(N_1\) and \(N_2\) as the magnitudes of the normal forces acting on the two sliding faces.

(1)\[\begin{split}N_1 &= \frac{- (\mathbf{A} \times \mathbf{n_2}) \times (\mathbf{n_1} \times \mathbf{n_2})} {\|\mathbf{n_1} \times \mathbf{n_2}\|^2} \\ N_2 &= \frac{- (\mathbf{A} \times \mathbf{n_1}) \times (\mathbf{n_1} \times \mathbf{n_2})} {\|\mathbf{n_1} \times \mathbf{n_2}\|^2}\end{split}\]

where \(n_i\) is the normal to the block face directed towards the interior of the block and \(\mathbf{A}\) is the total externally applied force acting on the block (in this example the block’s weight).

The total shear force along the sliding direction is given by:

(2)\[T_{12} = \mathbf{A} \times \mathbf{s_{12}}\]

where \(s_{12}\) is the sliding direction calculated from the intersection of the two sliding faces:

(3)\[s_{12} = \frac{(\mathbf{n_1} \times \mathbf{n_2})} { \|\mathbf{n_1} \times \mathbf{n_2}\|^2} \text{sgn}((\mathbf{n_1} \times \mathbf{n_2}) \cdot \mathbf{A})\]

In the absence of cohesion in the joint, and supposing the same angle of friction on both sliding faces, the safety factor can be calculated as

(4)\[F_s = \frac{(N_1+N_2) \tan{\phi}} {T_{12}}\]

The critical friction angle to have stability (minimum factor of safety of 1) can thus be deduced. In this example the critical friction angle is 33.36°. This value is computed using the Python script in the file analytical_fric.py.

Numerical Analysis

Starting from the system in equilibrium under gravity loading with very large friction, the friction angle of the two sliding faces is modified in order to find the minimum critical angle for which the block is stable, using a bisection algorithm written in Python. Every time the friction angle is changed the model is run to equilibrium with a maximum number of steps (maximum of 10000).

The block is considered stable for a given friction angle if the equilibrium (an average ratio of unbalanced forces 1e-6) is reached for a number of cycles inferior to the maximum. Otherwise the block is considered unstable. A python cycle in the bisection algorithm consists in restoring the initial state, testing the stability for a given friction angle – middle of the current interval of values– and dividing this interval by 2 based on the stability result. The solution of the critical friction angle is reached when the computation interval is inferior to a minimum (here we set 0.001).

Running this algorithm, we get a critical friction angle of 33.398°, thus an error of 0.128% comparing to the analytical solution.

References

[GoodmanShi1985]

Goodman, R. E. and Shi, G.,”Block Theory and its Application to Rock Engineering,” Prentice-Hall, London (1979).

Data Files

make_system.dat

model new
model large-strain on
model domain extent -2. 2. condition destroy
rblock create box -1. 1.
fracture create dip 40. dip-direction 130. position 0,0,1 size 5
fracture create dip 60. dip-direction 220. position 0,-0.25,1 size 5
rblock cut fractures

; Boundary conditions
[rblock.group(rblock.near(0.0477973,-0.786686,0.82332)) = 'free']
rblock fix velocity spin range group 'free' not

; Model Parameters
rblock attribute density 2000.0 damp 0.7
contact cmat default model linear ...
                     property kn 1.e7 ks 1.e7 fric 1.e20 lin_mode 1
; Gravity
model gravity 0,0,-9.81

; Monitoring
model history name 'aratio' mechanical ratio-average

; Settle under gravity loading to equilibrium state
model solve ratio-average 1e-5
model save 'ini.sav'
program return

analytical_fric.py

import itasca as it 
import math
import numpy as np
from vec import vec3 

it.command("""
    python-reset-state off
    model new
    model restore \'ini.sav\'
      """)

f1=it.dfn.fracture.find(1)
f2=it.dfn.fracture.find(2)


# find normals to the fractures 
n1=f1.normal()
n2=f2.normal()

#Normal orientated to the interior of the bloc
if f1.normal_z()<0:
    n1=-n1
if f2.normal_z()<0:
    n2=-n2

#Apply Goodman and Shi theory

#Active force vector
WW=348.074          #find inertial mass from rigid block python object ???
A=vec3((0,0,-WW))

#Calculating the sliding direction
n12=n1.cross(n2)
s12=n12/n12.mag()*np.sign(n12.dot(A))

#Normal forces 
N1=-(A.cross(n2)).dot(n12)/(n12.mag())**2
N2=-(A.cross(n1)).dot(-n12)/(n12.mag())**2
#Shear force
T12=A.dot(s12)

# Critical friction angle (if zero cohesion)
fric_theory=math.atan(T12/(N1+N2))*180./math.pi
print("Analytical critical friction angle is "+str(fric_theory)+" degrees")

pfc_fric.py

import itasca as it 
import math

fric_limit1 = 0.0
fric_limit2 = 90.

while True:

    it.command("""
    model new
    model restore \'ini.sav\'
    rblock attribute displacement 0
    rblock attribute velocity 0.
    rblock history name \'zdisp\' displacement-z position (0.0477973,-0.786686,0.82332)
    """)

    cycle_max = it.cycle() + 50000
  
    fric_angle = (fric_limit1 + fric_limit2)/2.
    it.command("""
                  [fric_angle = {}]
                  contact property fric [math.tan(fric_angle*math.pi/180.)])
                  model solve ratio-average 1e-6 cycles-total 10000
                  fish define isStable
                    isStable = false
                    if rblock.num == 4
                        if mech.cycle < 50000
                            isStable = true
                        endif
                    endif   
                  end
               """.format(fric_angle))
    
    if it.fish.call_function("isStable") is True: #stable
        fric_limit2 = fric_angle
        print("Stable for "+str(fric_angle) +" degrees")
        it.command("model save \'last_stable.sav\'")
    
    else : #unstable
        fric_limit1 = fric_angle
        print("Unstable for "+str(fric_angle) +" degrees")
        it.command("model save \'last_unstable.sav\'")
        
    #compute interval size
    min_interval = (fric_limit2 - fric_limit1)/2.
    if min_interval<0.001:
        break    
    
print("Last stable friction angle interval is ["
      + str("%.3f" % fric_limit1) +";"
      + str("%.3f" % fric_limit2)+"] (degrees)")
_error=abs(fric_limit2-fric_theory)/fric_theory*100.0
print("The error relative to the theoretical solution (" 
      + str("%.3f" % fric_theory)
      + ") is "+str("%.3f" % _error)+"%")

Endnote