Energy and Dissipation Mechanisms in PFC
Energy Tracking
Energy tracking is enabled with the model energy command. Energies are accumulated each cycle
for balls, clumps, walls, and contacts. Mechanical energies fall into two categories: body energies and contact energies.
These can be retrieved via the ball.energy, clump.energy, wall.energy, and
contact.energy FISH functions. The total energies falling into each category can be
retrieved with the mech.energy FISH function.
Mechanical body energies are those related to body motion. For balls and clumps, these energies are: the energy due to body forces, where body forces are defined to be gravity loading and applied forces and moments (denoted energy-body), the energy dissipated by local damping (denoted energy-damp) and the kinetic energy (denoted energy-kinetic). For walls, the boundary work (denoted energy-boundary) is accumulated. At each timestep, the boundary work is the sum of the dot product of the force on a wall and the incremental displacement, and the dot product of the moment on the wall with the incremental angular displacement.
Mechanical contact energies are those defined by the contact models. The list of mechanical contact models is given in the “Contact Models” section. In the documentation for each contact model, an Energies table exists. These include the linear, linear contact bond, linear parallel bond, hertz, hysteretic, smooth joint, and the flat joint energy tables. For all built-in contact models, the energy list includes: energy-adhesive, energy-dashpot, energy-pbstrain, energy-rrstrain, energy-rrslip, energy-slip, and energy-strain.
Mechanical Damping
Energy supplied to the particle system is dissipated, via contact models, through frictional sliding or viscous damping. However, these dissipation mechanisms may not be sufficient to arrive at a steady-state solution in a reasonable number of cycles. A body-based damping scheme termed local damping is available to remove additional kinetic energy. Local damping acts on each ball or clump, applying a damping force with magnitude proportional to the unbalanced force.
For compact assemblies, non-zero local damping may be used to establish equilibrium and to conduct quasi-static deformation simulations. When a dynamic simulation of a compact assembly is required, contact model based damping strategies are preferred and the local damping coefficient should be set to a 0.0 or a small value. For problems involving free flight of particles and/or impacts between particles, local damping is inappropriate and contact model based damping strategies should be used. If the simulation is dominated by rapid impacts, one should consider the use of the hysteretic contact model for realistic dissipation of energy.
Local Damping
The local damping used in PFC is similar to that described in [Cundall1987]. A damping-force term is added to the equations of motion (given here for translational motion and here for rotational motion) such that the damped equations of motion can be written as
where \({\cal F}_{(i)}\), \({\cal M}_{(i)}\), and \({\cal A}_{(i)}\) are the generalized force, mass, and acceleration components, respectively. \({\cal F}_{(i)}\) includes the contribution from the gravity force, and \(\mathbf{F^d}_{(i)}\) is the damping force:
expressed in terms of the generalized velocity:
The damping force is controlled by the damping constant \(\alpha\), whose default value is 0.0, and
which can be specified separately for each ball or clump using the damp keyword in the
ball attribute or clump attribute commands, respectively.
This form of damping has the following advantages:
Only accelerating motion is damped; therefore, no erroneous damping forces arise from steady-state motion.
The damping constant, \(\alpha\), is nondimensional.
Since damping is frequency-independent, regions of the assembly with different natural periods are damped equally, using the same damping constant.
Similarity to Hysteretic Damping
The local damping formulation is similar to hysteretic damping, in which the energy loss per cycle is independent of the rate at which the cycle is executed. This similarity is demonstrated in the following analysis. Upon examination of Equation (2), it is evident that the damping force always opposes motion, but it is scaled to the resultant generalized force, unlike viscous damping, which is scaled to the magnitude of velocity. Two forms of Equation (1) may be written depending on the relative signs of \({\cal F}_{(i)}\) and \({\cal V}_{(i)}\). When they are of the same sign, the equation of motion is
and when they are of opposite signs, the equation of motion is
These equations may be written in terms of apparent mass as
where \({\cal M}_{(i)}^+ = {\cal M}_{(i)} / (1-\alpha)\) and \({\cal M}_{(i)}^- = {\cal M}_{(i)} / (1+\alpha)\).
The motion of the single degree-of-freedom mass-spring system from this figure in the “Timestep Determination” section, when given an initial displacement such that \(x = a\) at \(t = 0\), is shown in the figure below. For such motion, the apparent mass is increased at the two times in each cycle when the velocity is zero, and reduced at the two times when the velocity is maximum. The damping operates by removing kinetic energy twice per cycle. At the point of peak velocity, part of the moving mass is removed and discarded. Note that there is no discontinuity in acceleration, since the acceleration is zero at the instant when mass is removed. The amount of energy removed per cycle is given by twice the drop in kinetic energy at point \(B\) or
and the mean kinetic energy at the instant of removal is
where \({\cal V}_{(i)}\) is the generalized velocity given by Equation (3).
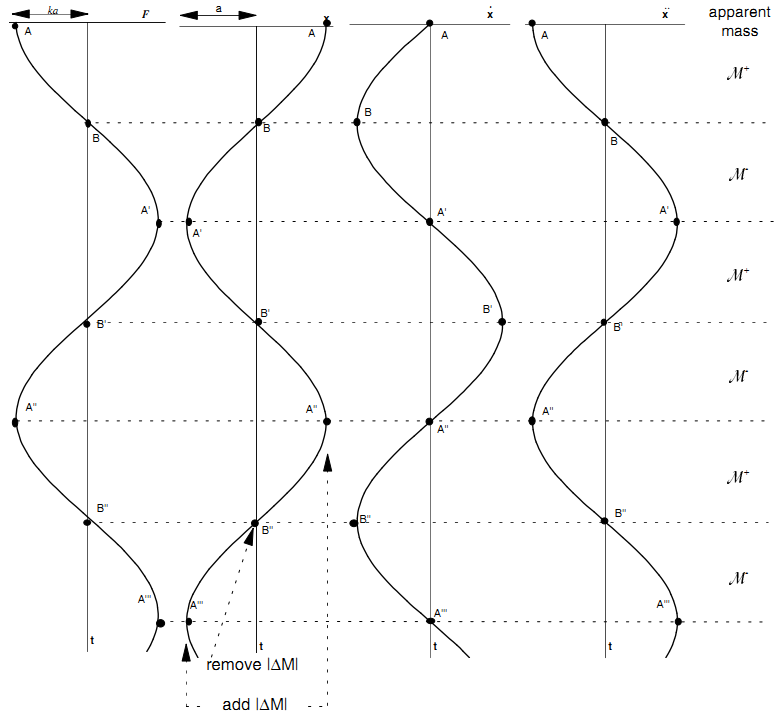
Figure 1: Motion of single mass-spring system.
The ratio of energy lost per cycle to maximum energy stored is called the “specific loss” ([Kolsky1963]). The specific loss can be written in terms of the damping constant by noting that, for a single degree-of-freedom system, or for oscillation in a single mode, the peak kinetic energy is the same as the peak stored energy. Thus, the specific loss can be written as
The fraction of critical damping, \(D\), can be written in terms of the specific loss for small values of damping by
For the value \(\alpha = 0.7\), the approximate fraction of critical damping is therefore 0.22.
Equation (9) can be verified by loading one and three stacked particles, respectively, by suddenly applied gravity, and allowing each system to oscillate to equilibrium. Both tests give approximately the same value for \(\Delta W / W\), confirming that the damping is independent of frequency. However, for a system where multiple modes are active simultaneously, the response computed by PFC may not show the same damping for each mode.
Local damping is inappropriate for particles in free flight under gravity. Local damping may also be inappropriate for systems in which large groups of particles are driven by specified-velocity boundary conditions.
References
Cundall, P. A. “Distinct Element Models of Rock and Soil Structure,” in Analytical and Computational Methods in Engineering Rock Mechanics, Ch. 4, pp. 129-163. E. T. Brown, ed. London: Allen & Unwin., 1987.
Kolsky, H. Stress Waves in Solids. New York: Dover Publications, 1963.
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: May 07, 2024 |
