Uniaxial Compression and Extension Tests with Concrete Model
Note
The project file for this example may be viewed/run in 3DEC.[1] The data files used are shown at the end of this example.
In this example to test the Concrete model, a 1 m x 1 m single hexahedral zone is generated, and the material properties are listed in Table 1. The model behavior is compared to laboratory data from Lee and Fenves (1998).
Parameter |
Value |
|---|---|
\(E\) (MPa) |
3.14e4 |
\(\nu\) |
0.18 |
\(f_t^m\) (MPa) |
3.48 |
\(f_t^0\) (MPa) |
3.48 |
\(G_t\) (MN/m) |
40e-6 |
\(l_t\) (m) |
0.0826 |
\(D_t^{half}\) |
0.5 |
\(f_c^m\) (MPa) |
27.6 |
\(f_c^0\) (MPa) |
16.04 |
\(G_c\) (MN/m) |
5690e-6 |
\(l_c\) (m) |
0.0826 |
\(D_c^{peak}\) |
0.4 |
\(f_b^0/f_c^0\) |
1.16 |
\(a_p\) |
0.2 |
\(s_0\) |
0.2 |
The first test is the uniaxial compression loading. The 3DEC results compared to the laboratory results are shown in Figure 1. The numerical model correctly duplicated the whole loading, which can be verified by the elastic slope (Young’s modulus), initial and peak compression yield stress.
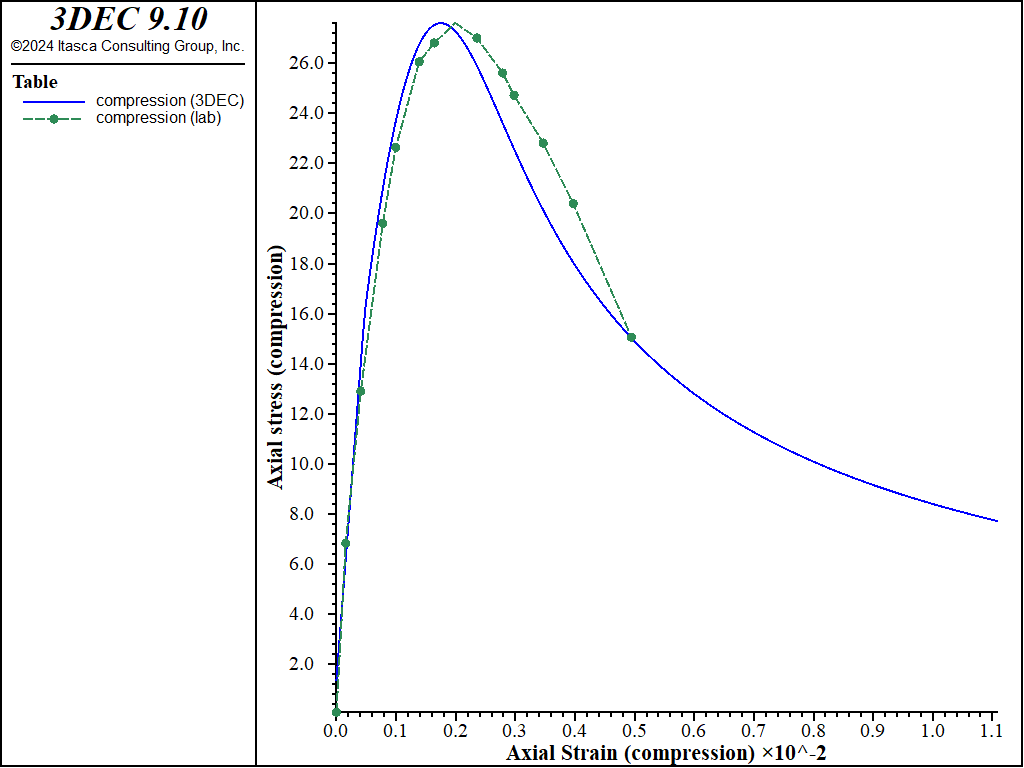
Figure 1: Uniaxial stress vs. uniaxial strain in compression. Compression is positive.
The second test is the uniaxial tension loading. The 3DEC results compared to lab results are shown in Figure 2. Since \(f_t^0=f_t^m\), the uniaxial tension stress vs train curve has immediate softening, which has been correctly simulated by the numerical model the whole loading.
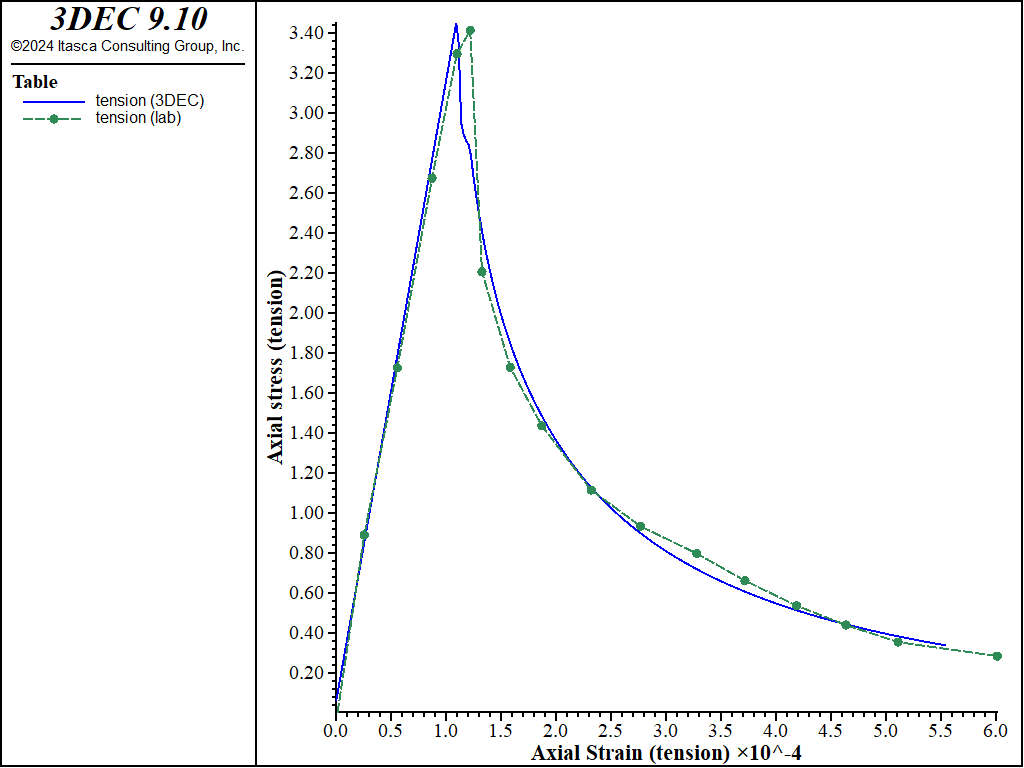
Figure 2: Uniaxial stress vs. uniaxial strain in extension.
References
Lee, J., & Fenvas, G. L. (1998). Plastic-damage model for cyclic loading of concrete structures. Journal of engineering mechanics, 124(8), 892-900.
Data File
uniaxialCompression.dat
model new
model large-strain off
;
fish define parameters
global young = 3.1e4 ; MPa
global poisson = 0.18
global ft = 3.48 ; MPa
global Gt = 40e-6 ; MN/m
global Lt = 0.0826 ; m
global fc = 27.6 ; MPa
global ft = 3.48 ; MPa
global Gc = 5690e-6 ; MN/m
global Lc = 0.0826 ; m
global kbc0 = 1.16
global fc0 = 16.04 ; MPa
global ft0 = 3.48 ; MPa
global dc = 800 ; dc
global dt = 3000 ; dt
end
[parameters]
;
block create brick 0 1
block zone generate hexahedra divisions 1 1 1
;block zone generate-new maximum-edge 0.25
;block zone nodal-mixedip-directionisc on
block gridpoint group 'top' range position-z 1
[global gpsTop = list(block.gp.list)(block.gp.isgroup(::block.gp.list,"top"))]
block zone cmodel assign concrete
block zone property density 2500 young [young] poisson [poisson]
block zone property compression-strength [fc] compression-initial [fc0] ...
compression-energy-fracture [Gc]
block zone property compression-length-reference [Lc] compression-d [dc]
block zone property tension-strength [ft] tension-initial [ft0] ...
tension-energy-fracture [Gt]
block zone property tension-length-reference [Lt] tension-d [dt]
block zone property ratio-biaxial [kbc0] tension-recovery 0.2
block zone property dilation 20
block gridpoint apply velocity-z 0 range position-z 0
[gptr = block.gp.near(1,1,1)]
fish define szz
strain = -block.gp.disp(gptr)->z
szz = -list.sum(block.gp.force.reaction(::gpsTop)->z)
end
history interval 200
fish history name 'strain' strain
fish history name 'szz' szz
block gridpoint apply velocity-z -5e-6 range group 'top'
model step 50000
history export 'szz' vs 'strain' table 'compression-3dec'
table 'compression-3dec' export 'compression-3dec' truncate
model save 'uniaxial-Compression'
uniaxialTension.dat
model new
model large-strain off
;
fish define parameters
global young = 3.1e4 ; MPa
global poisson = 0.18
global ft = 3.48 ; MPa
global Gt = 40e-6 ; MN/m
global Lt = 0.0826 ; m
global fc = 27.6 ; MPa
global ft = 3.48 ; MPa
global Gc = 5690e-6 ; MN/m
global Lc = 0.0826 ; m
global kbc0 = 1.16
global fc0 = 16.04 ; MPa
global ft0 = 3.48 ; MPa
global dc = 800 ; dc
global dt = 3000 ; dt
end
[parameters]
block create brick 0 1
block zone generate hexahedra divisions 1 1 1
;block zone generate-new maximum-edge 0.25
;block zone nodal-mixedip-directionisc on
block gridpoint group 'top' range position-z 1
[global gpsTop = list(block.gp.list)(block.gp.isgroup(::block.gp.list,"top"))]
block zone cmodel assign concrete
block zone property density 2500 young [young] poisson [poisson]
block zone property compression-strength [fc] compression-initial [fc0] ...
compression-energy-fracture [Gc]
block zone property compression-length-reference [Lc] compression-d [dc]
block zone property tension-strength [ft] tension-initial [ft0] ...
tension-energy-fracture [Gt]
block zone property tension-length-reference [Lt] tension-d [dt]
block zone property ratio-biaxial [kbc0] tension-recovery 0.2
block zone property dilation 20
block gridpoint apply velocity-z 0 range position-z 0
[gptr = block.gp.near(1,1,1)]
fish define szz
strain = block.gp.disp(gptr)->z
szz = list.sum(block.gp.force.reaction(::gpsTop)->z)
end
history interval 100
fish history name 'strain' strain
fish history name 'szz' szz
block gridpoint apply velocity-z 5e-7 range group 'top'
model step 25000
history export 'szz' vs 'strain' table 'tension-3dec'
table 'tension-3dec' export 'tension-3dec' truncate
model save 'uniaxial-Tension'
Endnote
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Aug 13, 2024 |
