Reinforced Concrete Beam

Problem Statement

Note

The project file for this example may be viewed/run in 3DEC.[1] The data files used are shown at the end of this example.

Problem Description

This example simulates the bending of a concrete beam supported by steel cables. The model demonstrates the use of the Concrete Constitutive Model.

3DEC Model

Model Geometry

The beam is 10x10x100 cm and a zone size of 5 mm is used. The 3DEC model is shown in Figure 1. Three cables are installed inside the beam, close to the bottom as shown in Figure 2. The ends of each cable are rigidly attached to the grid.

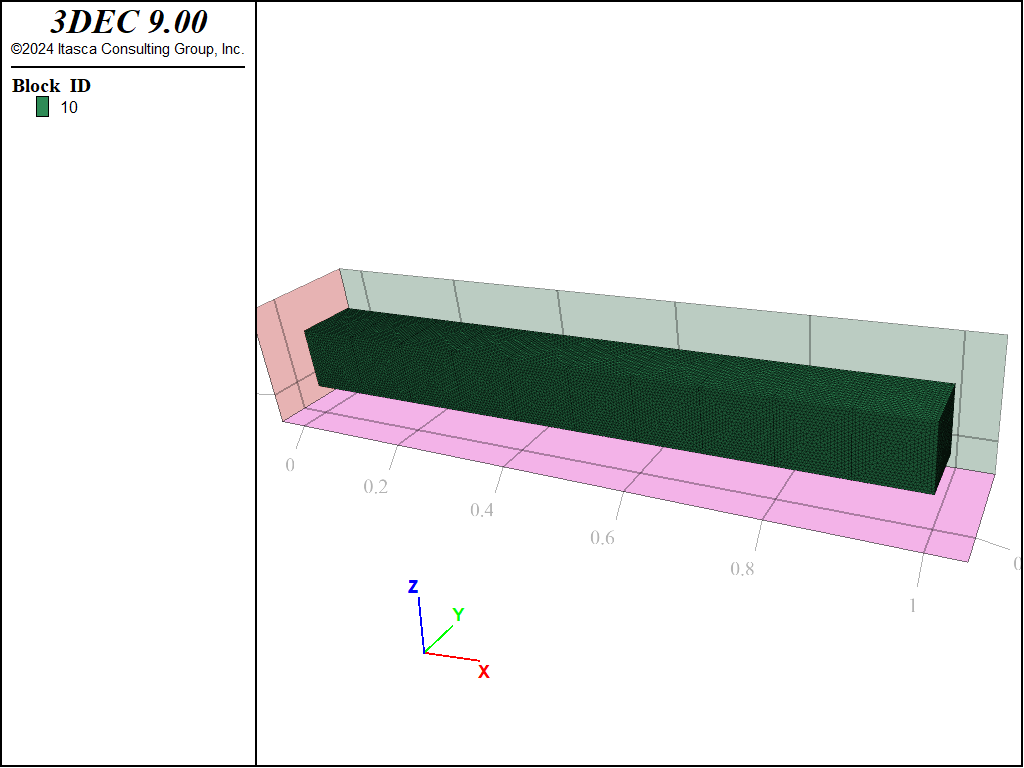
Figure 1: 3DEC concrete beam model.

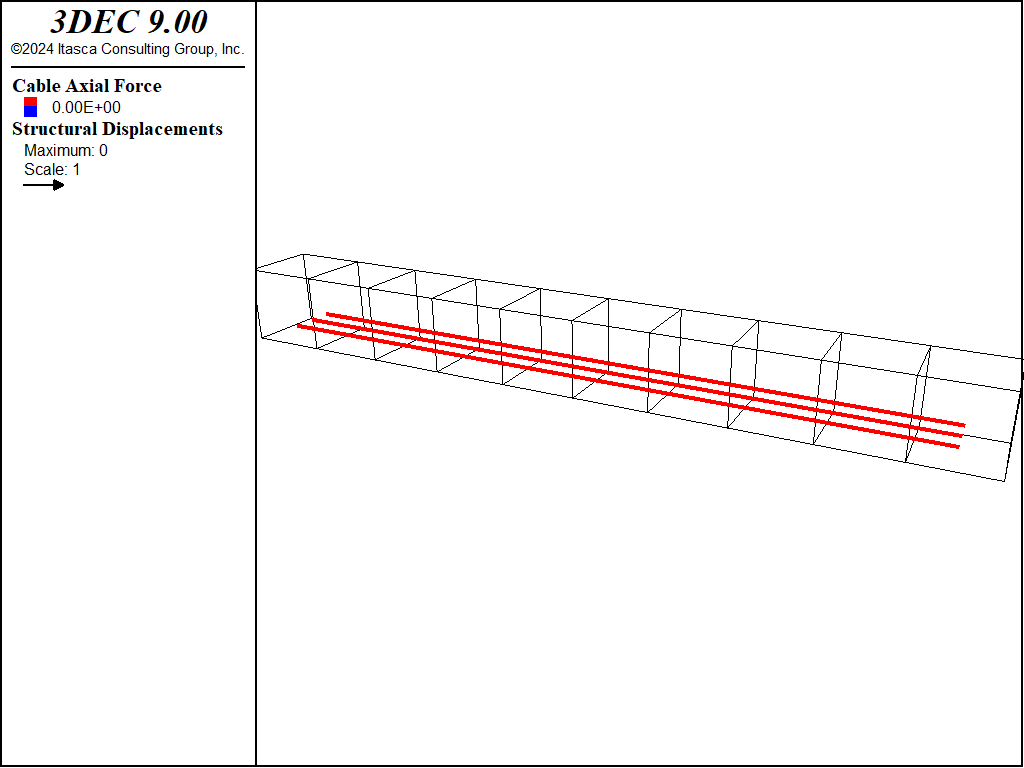
Figure 2: Cables in the beam model.

Properties

The concrete material properties are shown in Table Table #3decconcrete-properties. The cable properties are in Table Table #3deccable-properties

Table 1: Concrete Model Properties

Parameter	Value
Young’s modulus, \(E\) (MPa)	3100
Poisson’s ratio, \(\nu\)	0.18
Uniaxial tension maximum strength, \(f_t^m\) (MPa)	3.48
Uniaxial tension initial strength, \(f_t^0\) (MPa)	3.48
Uniaxial tension fracture energy, \(G_t\) (MN/m)	40e-6
Uniaxial tension reference length, \(l_t\) (m)	0.00826
Uniaxial compression maximum strength, \(f_c^m\) (MPa)	27.6
Uniaxial compression initial strength, \(f_c^0\) (MPa)	16.04
Uniaxial compression fracture energy, \(G_c\) (MN/m)	5690e-6
Uniaxial compression reference length, \(l_c\) (m)	0.00826
Compression damage parameter, \(d_c^{peak}\)	800
Biaxial-Uniaxial compression strength ratio, \(f_b^0/f_c^0\)	1.16

Table 2: Cable Properties

Parameter	Value
Young’s modulus (MPa)	2e5
Cross-sectional area (m^2)	1.27e-4
Grout stiffness (MN/m/m)	1e6
Ground friction angle (degrees)	25
Grout cohesion (MN/m)	0.1 MN/m
Grout perimeter (mm)	40

Model Solving

The beam is simply supported along two lines on the bottom and velocities are applied to two points on top of the beam to induce bending. The geometry of the fixities and applied velocities are shown in Figure 3. Reaction forces were recorded at the location of the applied velocities.

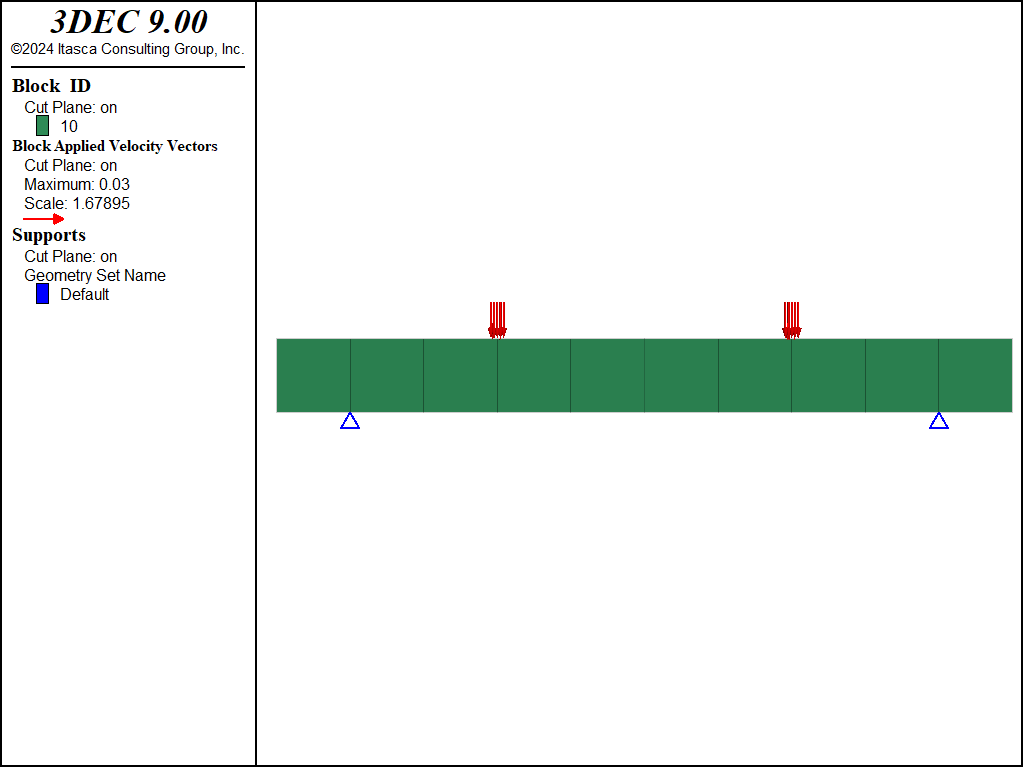
Figure 3: Cross-section of the beam showing loads and fixities.

The model was then cycled for 90,000 steps.

Results and Discussion

The shear strain after 90,000 steps is shown in Figure 4. The deformations are exaggerated 50x to show the nature of deformation. The zones of high shear strain correspond to areas of high damage as shown in Figure 5.

A history of applied load (the average of the reaction forces at the two locations velocity is applied) is shown in Figure 6. The peak load for the beam is about 0.023 MN.

The axial forces in the cables are shown in Figure 7. Since most of the deformation in the cables is vertical (bending), the axial forces are relatively small. There is no failure in either the cables or the grout.

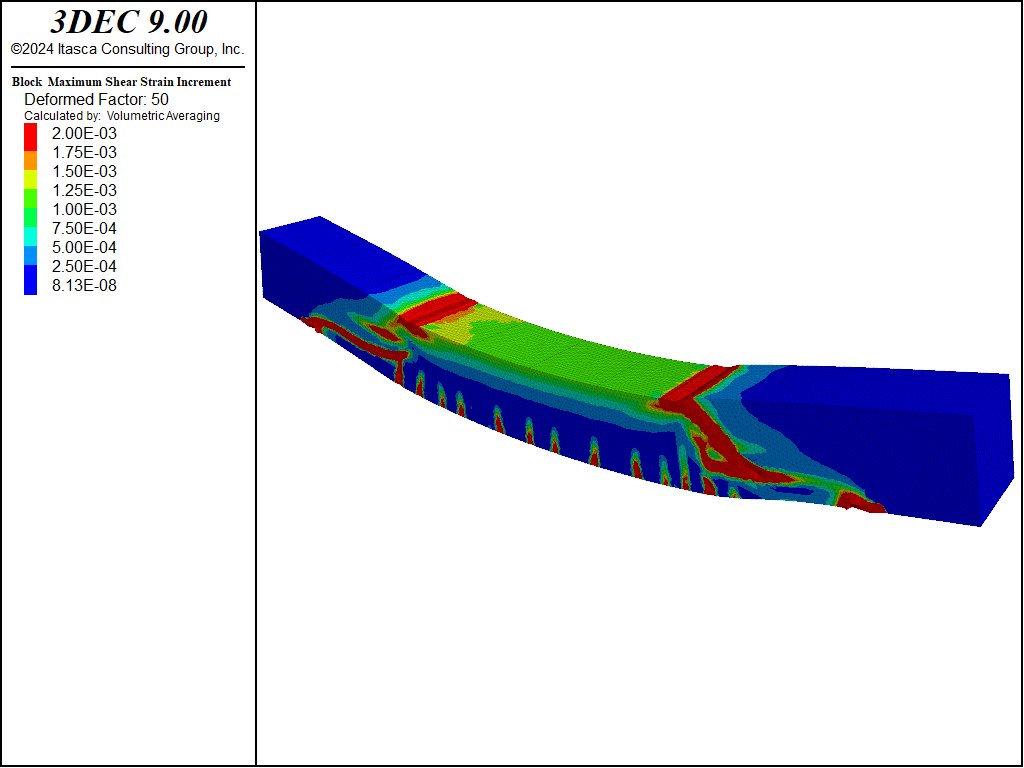
Figure 4: Shear strain in the model after 90,000 steps.

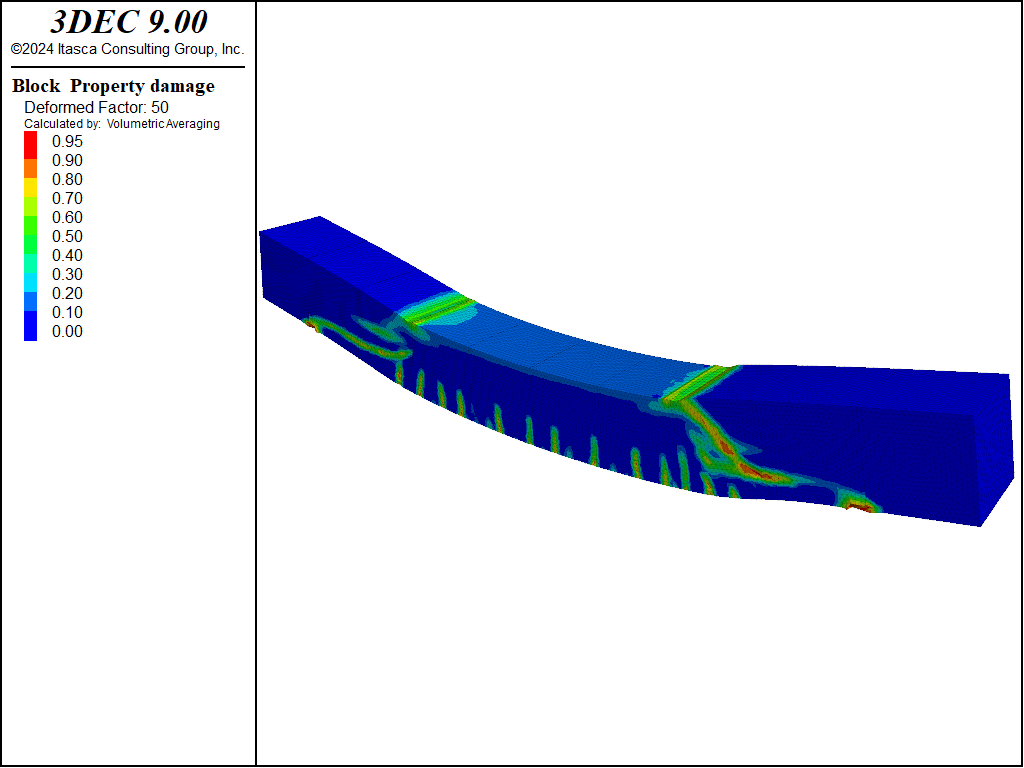
Figure 5: Damage in the model after 90,000 steps.

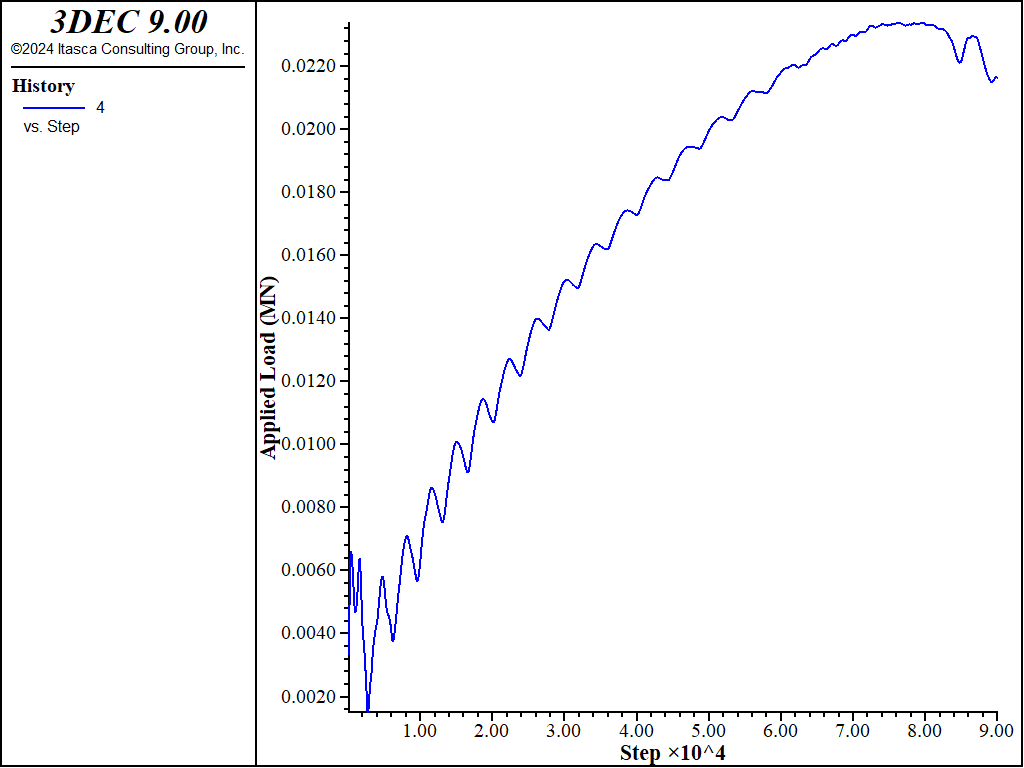
Figure 6: History of applied load.

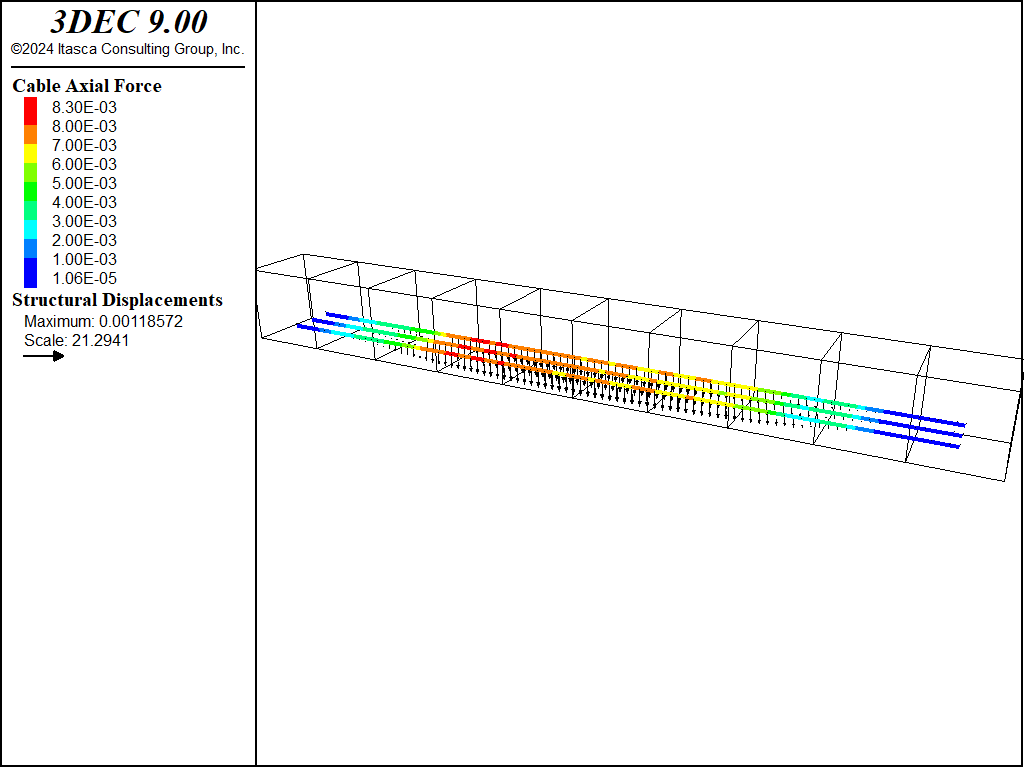
Figure 7: Axial forces in the cables.

Data Files

beam.dat

model new
model large-strain off

block create brick 0 1 0 0.1 0 0.1

; multi-threading is block based.  So divide this up for efficiency
block densify segments 10 1 1 join
block zone generate-new maximum-edge 0.005

fish define parameters
    global dens = 2500e-6   ; kg/m3 x 10^-6
    global young = 3.1e4  ; MPa
    global poisson = 0.18 
    global ft = 3.48      ; MPa
    global Gt = 40e-6     ; MN/m
    global Lt = 0.0826/10 ; m
    global fc = 27.6      ; MPa
    global Gc = 5690e-6   ; MN/m
    global Lc = 0.0826/10 ; m  
    global kbc0 = 1.16 
    global fc0 = 16.04    ; MPa
    global ft0 = 3.48     ; MPa 
    global dc = 800       ; dc
    global dt = 3000      ; dt
end
[parameters]
;
block zone cmodel assign concrete
block zone property density [dens] young [young] poisson [poisson]
block zone property compression-strength [fc] compression-initial [fc0]  
block zone property compression-length-reference [Lc] compression-d [dc] 
block zone property tension-strength [ft] tension-initial [ft0] 
block zone property compression-energy-fracture [Gc] tension-energy-fracture [Gt] 
block zone property tension-length-reference [Lt] tension-d [dt]
block zone property ratio-biaxial [kbc0] tension-recovery 0.2 ;ratio-dilation 0.2
block zone property dilation 20

structure cable create by-line (0.05, 0.02, 0.02) (0.95, 0.02, 0.02) ...
  segments 90 group-begin "end1" group-end "end2" group "steel" id 1
structure cable create by-line (0.05, 0.05, 0.02) (0.95, 0.05, 0.02) ...
  segments 90 group-begin "end1" group-end "end2" group "steel" id 1
structure cable create by-line (0.05, 0.08, 0.02) (0.95, 0.08, 0.02) ...
  segments 90 group-begin "end1" group-end "end2" group "steel" id 1

structure link attach x rigid y rigid z rigid range group "end1"
structure link attach x rigid y rigid z rigid range group "end2"

structure cable property young 2e5 cross-sectional-area 1.27e-4 ...
  grout-stiffness 1e6 grout-friction 25 grout-cohesion 0.1 ...
  grout-perimeter 0.04

; point loads
block gridpoint group "Load1" range position-x 0.29 0.31 position-z 0.1
block gridpoint group "Load2" range position-x 0.69 0.71 position-z 0.1
[global LoadedPts1 = block.gp.list(block.gp.isgroup(::block.gp.list,"Load1"))]
[global LoadedPts2 = block.gp.list(block.gp.isgroup(::block.gp.list,"Load2"))]

fish define load
    load1 = list.sum(block.gp.force.reaction(::LoadedPts1)->z)
    load2 = list.sum(block.gp.force.reaction(::LoadedPts2)->z)
    load  = -0.5*(load1 + load2)
end

; fix points on bottom
block gridpoint apply velocity (0,0,0) range position-x 0.09 0.11 position-z 0
block gridpoint apply velocity (0,0,0) range position-x 0.89 0.91 position-z 0

; point loads
block gridpoint apply velocity-z -0.03 range group "Load1"
block gridpoint apply velocity-z -0.03 range group "Load2"

history interval 100
block history displacement-z position 0.5 0.05 0
history fish load1
history fish load2
history fish load

model save 'initial'

; damp local works better when there are no joints
block mechanical damping local  
block zone nodal-mixed-discretization on
model cycle 90000

model save 'beam'

Endnote

[1]

This example is listed under the present document title in the i Examples dialog use the menu command Help -> Examples… to access.