Cylindrical Hole in an Infinite Elastic Medium

Problem Statement

Note

To view this project in 3DEC, use the menu command Help ► Examples…. The main data files used are shown at the end of this example. All data files are found in the project.

This problem concerns the determination of stresses and displacements around a cylindrical hole in an infinite elastic medium subjected to an in-situ stress field. The problem tests the isotropic elastic material model.

A 1.0 m radius cylindrical hole in an infinite body is subjected to a compressive, anisotropic state of stress: a vertical stress of 30 MPa and a horizontal stress of 15 MPa. The following material properties are assumed:

shear modulus (\(G\)): 2.8 GPa

bulk modulus (\(K\)): 3.9 GPa

density (\(\rho\)): 2600 kg/m³

It is assumed that the radius is small compared to the length of the cylinder, which makes it possible to compare the 3D problem to a 2D plane-strain solution.

Analytic Solution

The displacements and stresses around a circular hole in an infinite, isotropic, linearly elastic medium are given by the classical Kirsch solution (e.g., see Jaeger and Cook 1976).

The stresses \(\sigma_r\), \(\sigma_\theta\), and \(\tau_{r\theta}\), at a point with polar coordinates (\(r\), \(\theta\)) relative to the center of the opening with radius \(a\) (Figure 1), are:

\[\sigma_r\ =\ {p_1 + p_2 \over {2}}\ \left(1 - {a^2 \over r^2} \right)\ +\ {p_1 - p_2 \over {2}}\ \left( 1 - {4a^2 \over {r^2}} + {3a^4 \over {r^4}} \right)\ \cos 2\theta\]

\[\sigma_\theta\ =\ {p_1 + p_2 \over {2}}\ \left(1 + {a^2 \over r^2} \right) - {p_1 - p_2 \over {2}}\ \left( 1 + {3a^4 \over {r^4}} \right) \cos 2\theta\]

\[\tau_{r\theta} = - {p_1 - p_2 \over {2}}\ \biggl( 1 + {2a^2 \over {r^2}} - {3a^4 \over {r^4}} \biggr)\ \sin 2\theta\]

The displacements can also be determined assuming conditions of plane strain:

\[u_r = {p_1 + p_2 \over {4G}}\ {a^2 \over {r}} + {p_1 - p_2 \over {4G}}\ {a^2 \over {r}}\ \biggl[ 4 (1 - \nu) - {a^2 \over {r^2}} \biggr]\ \cos 2\theta\]

\[u_\theta = - {p_1 - p_2 \over {4G}}\ {a^2 \over {r}}\ \biggl[ 2 (1 - 2\nu) + {a^2 \over {r^2}} \biggr]\ \sin 2\theta\]

in which \(u_r\) is the radial outward displacement, \(u_\theta\) is the tangential displacement (as shown in Figure 1), and \(\nu\) is the Poisson’s ratio. The analytical solutions for both the stresses and the displacements are implemented in FISH functions listed in “ElasticHole.fis”.)

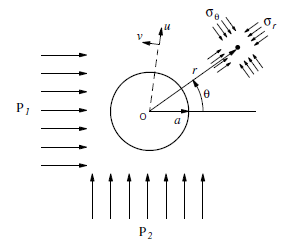
Figure 1: Cylindrical hole in an infinite elastic medium.

3DEC Models

The geometry of the 3DEC model used for this analysis is shown in Figure 2. The model is constrained in the direction of the \(x\)-axis, so that it can only move in the \(yz\)-plane (plane-strain condition). The model consists of 100 joined blocks in a radial pattern. The boundary was selected at 10 m (i.e., five hole-diameters) from the hole center. The problem was solved using three different zoning types. In the first case, a mixed-discretization (hex) zoning was used to discretize 100 blocks into 1000 zones. Figure 3 shows the geometry of blocks and zones for this case. (There is one hex zone – i.e., two sets of 5 overlapping tetrahedra per block.) In the second case, 100 blocks were discretized into 5689 “regular” tetrahedral zones. The geometry of the zones on one side of the model is shown in Figure 4. In the third case, the 100 blocks were discretized into 5689 high-order zones. In all cases, the blocks were joined (i.e., the discontinuities between blocks have no effect on deformation of the model).

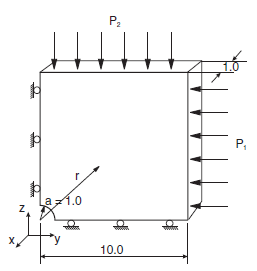
Figure 2: 3DEC model geometry used for analysis of a cylindrical hole in an elastic medium.

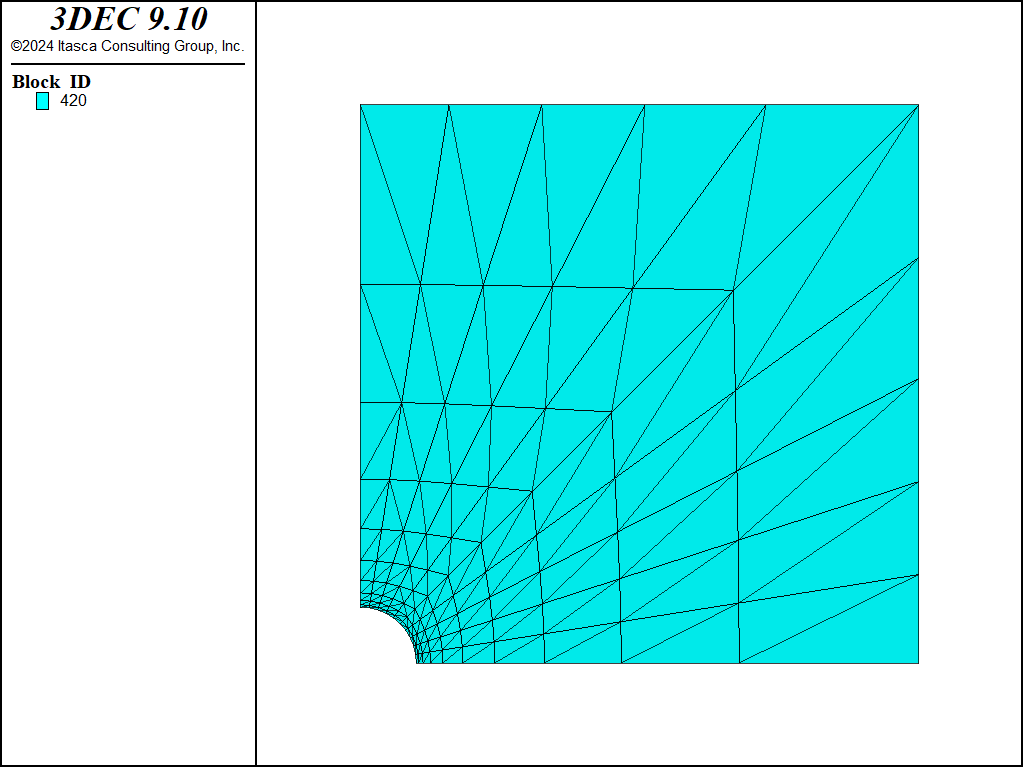
Figure 3: Blocks and “quad” zones in 3DEC model.

Figure 4: Tetrahedral zones in 3DEC model.

Results and Discussion

Vertical displacements along the \(y\)-axis are extracted from three 3DEC models and compared with analytical solutions. The comparison is shown in Figure 6, Figure 7, and Figure 8. Numerical results obtained with two different zonings of the model show excellent agreement with the analytical results, up to a distance of 2.5 radii from the center of the opening. The error at larger distances from the center of the opening is a consequence of the finite size of the models and the approximate boundary conditions.

Contours of normal vertical stress \(\sigma_{yy}\), calculated numerically for three cases of model zoning, are compared with analytical solutions in Figure 9, Figure 10, and Figure 11. Again, numerical results agree very well with the analytical solutions in the vicinity of the opening.

This verification problem demonstrates that 3DEC can be used for accurate calculation of stresses and deformations in continuous, elastic media. “Regular” tetrahedral, high-order tetrahedral and “hex” zoning yield accurate results, although hex zoning requires a smaller number of zones in order to achieve the same accuracy.

Figure 5: High-order tetrahedral zones in 3DEC model.

Figure 6: Comparison of vertical displacements along the \(y\)-axis using “hex” zones.

Figure 7: Comparison of vertical displacements along \(y\)-axis using tetrahedral zones.

Figure 8: Comparison of vertical displacements along \(y\)-axis using high-order tetrahedral zones.

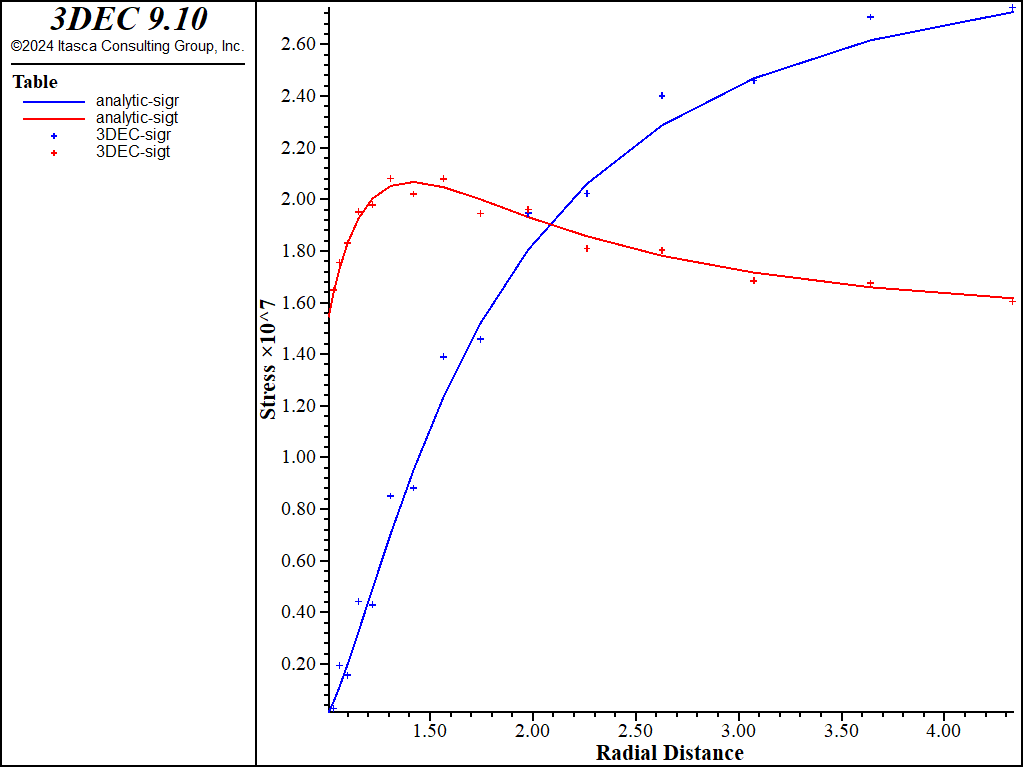
Figure 9: Comparison of \(\sigma_{yy}\) using “hex” zones.

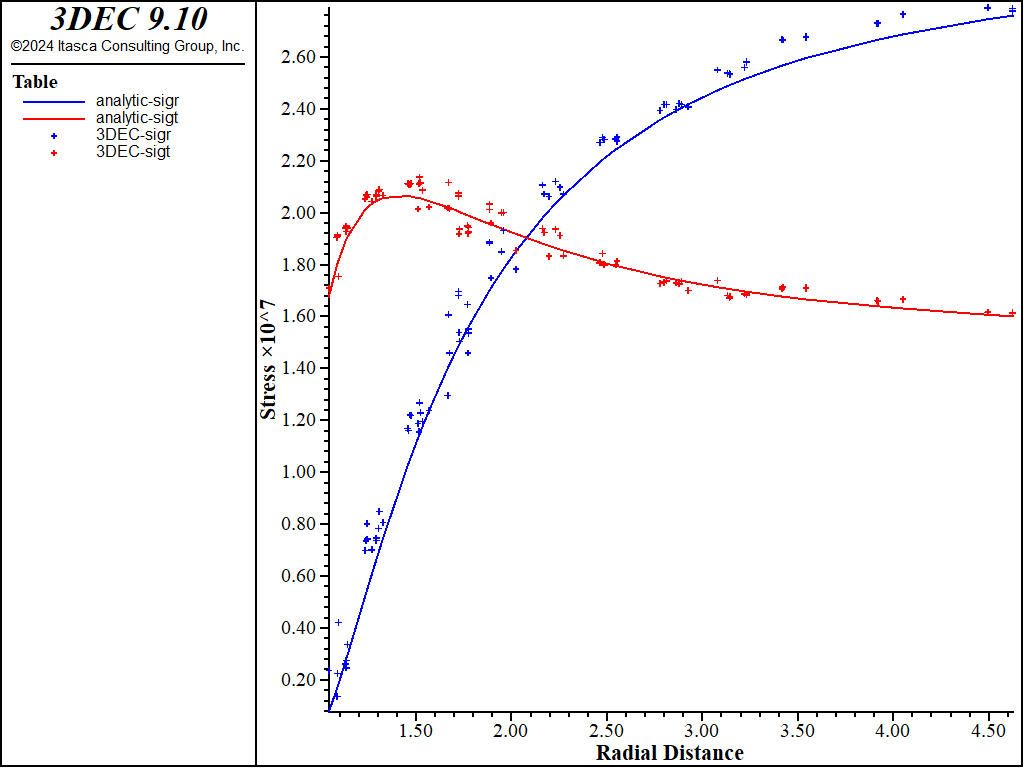
Figure 10: Comparison of \(\sigma_{yy}\) using tetrahedral zones.

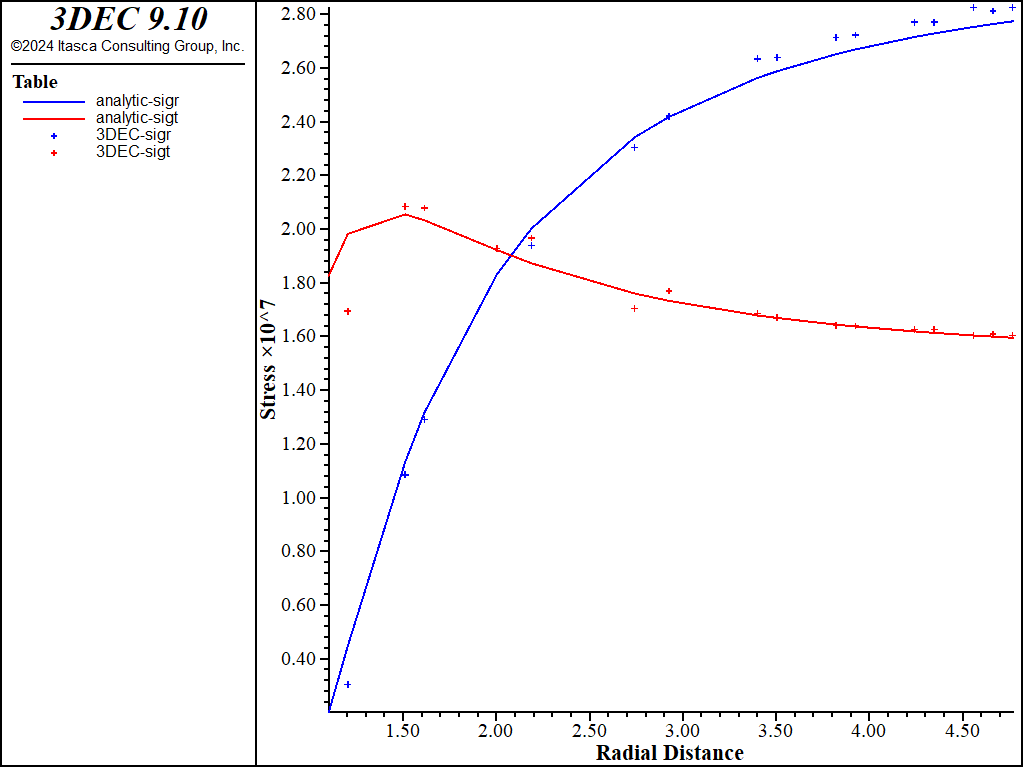
Figure 11: Comparison of \(\sigma_{yy}\) using high-order tetrahedral zones.

Reference

Jaeger, J. C., and N. G. W. Cook. Fundamentals of Rock Mechanics, 3rd Ed. London: Chapman and Hall (1976).

Data Files

ElasticHole-Hex.dat

;==========================================================================
; verification test -- 3dec modeling cylindrical hole in an infinite,
;                      isotropic, homogeneous, elastic medium
; quadrilateral zoning
; elastic blocks
;
;==========================================================================
model new

model large-strain off

block create tunnel dip 0 dip-direction 0 radius 1 length 0 1 ...
                    blocks-axial 1 blocks-radial 10 blocks-tangential 5 ...
                    boundary 9 radius-ratio 1.4
block delete range cylinder end-1 0 0 0 end-2 0 1 0 radius 0 1
block delete range plane dip 0 dip-direction 0 below
block delete range plane dip 90 dip-direction 90 below

block join on
;
; --- zoning of blocks ---
;
block zone generate hexahedra divisions 1 1 1
;
; --- material properties ---
;
block zone cmodel assign elastic
block zone property bulk 3.9e9 shear 2.8e9 density 2600 
;
; --- boundary conditions ---
block face apply stress -30e6 -30e6 -15e6 0 0 0 range position-x 10
block face apply stress -30e6 -30e6 -15e6 0 0 0 range position-z 10
block gridpoint apply velocity-x 0 range position-x 0
block gridpoint apply velocity-y 0 range position-y 0
block gridpoint apply velocity-y 0 range position-y 1
block gridpoint apply velocity-z 0 range position-z 0
;
;
; --- initial conditions ---
;
block insitu stress -30e6 -30e6 -15e6 0 0 0
;
model history mechanical unbalanced-maximum
;
model cycle 2000
program call 'ElasticHole.fis'
model save 'ElasticHole-Hex'
;
program return

ElasticHole-tet.dat

;==========================================================================
; verification test -- 3dec modeling cylindrical hole in an infinite,
;                      isotropic, homogeneous, elastic medium
; tetrahedral zoning
; elastic blocks
;
;==========================================================================
model new

model large-strain off

block create tunnel dip 0 dip-direction 0 radius 1 length 0 1 ...
                    blocks-axial 1 blocks-radial 4 blocks-tangential 5 ...
                    boundary 9 radius-ratio 1.4
block delete range cylinder end-1 0 0 0 end-2 0 1 0 radius 0 1
block delete range plane dip 0 dip-direction 0 below
block delete range plane dip 90 dip-direction 90 below

block join on
;
; --- zoning of blocks ---
;
block zone generate edgelength 0.2 range position-x 0.0 1.7 position-z 0.0 1.7
block zone generate edgelength 0.3 range position-x 0.0 2.9 position-z 0.0 2.9
block zone generate edgelength 0.5 range position-x 0.0 5.3 position-z 0.0 5.3
block zone generate edgelength 0.8
;
; --- material properties ---
;
block zone cmodel assign elastic
block zone property bulk 3.9e9 shear 2.8e9 density 2600 

;
; --- boundary conditions ---
block face apply stress -30e6 -30e6 -15e6 0 0 0 range position-x 10
block face apply stress -30e6 -30e6 -15e6 0 0 0 range position-z 10
block gridpoint apply velocity-x 0 range position-x 0
block gridpoint apply velocity-y 0 range position-y 0
block gridpoint apply velocity-y 0 range position-y 1
block gridpoint apply velocity-z 0 range position-z 0
;
; --- initial conditions ---
;
block insitu stress -30e6 -30e6 -15e6 0 0 0
;
model history mechanical unbalanced-maximum
;
model cycle 2000

program call 'ElasticHole.fis'

model save 'ElasticHole-tet'
;
program return

ElasticHole-HO.dat

;==========================================================================
; verification test -- 3dec modeling cylindrical hole in an infinite,
;                      isotropic, homogeneous, elastic medium
; tetrahedral zoning --- higher order zones
; elastic blocks
;
;==========================================================================
model new
model configure highorder

model large-strain off

block create tunnel dip 0 dip-direction 00 radius 1 length 0 1 ...
                    blocks-axial 1 blocks-radial 4 blocks-tangential 5 ...
                    boundary 9 radius-ratio 1.4
block delete range cylinder end-1 0 0 0 end-2 0 1 0 radius 0 1
block delete range plane dip 0 dip-direction 0 below
block delete range plane dip 90 dip-direction 90 below

block join on

; --- zoning of blocks ---
block zone generate edgelength 1.0
block zone generate high-order-tetra
;
; --- material properties ---
;
block zone cmodel assign elastic
block zone property bulk 3.9e9 shear 2.8e9 density 2600 

;
; --- boundary conditions ---
block face apply stress -30e6 -30e6 -15e6 0 0 0 range position-x 10
block face apply stress -30e6 -30e6 -15e6 0 0 0 range position-z 10
block gridpoint apply velocity-x 0 range position-x 0
block gridpoint apply velocity-y 0 range position-y 0
block gridpoint apply velocity-y 0 range position-y 1
block gridpoint apply velocity-z 0 range position-z 0
;
; --- initial conditions ---
;
block insitu stress -30e6 -30e6 -15e6 0 0 0
;
model history mechanical unbalanced-maximum
;
model cycle 2000

program call 'ElasticHole.fis'

model save 'ElasticHole-HO'
;
program return

ElasticHole.fis

;---------------------------------------------------------------------
;    exact and numerical solution processing for elastic hole problem
;
;    nastr, stores in
;    Table 1: analytical values rad/a -sigr
;    Table 2: analytical values rad/a -sigt
;    Table 3: numerical values rad/a -sigr
;             at zone centroid closest to x axis
;    Table 4: numerical values rad/a -sigt
;             at zone centroid closest to x axis
;
;    and calculates in whole grid
;    errsr  : average %error in -sigr
;    errst  : average %error in -sigt
;
;    nadis, stores in
;    Table 5: analytical values of rad/a -ur/a
;    Table 6: numerical  values of rad/a -ur/a at grid points on x axis
;
;    and calculates in whole grid
;    errd   : average %error in modulus of displacement
;---------------------------------------------------------------------
fish automatic-create off
;
;--- access properties and stresses ---
fish define props
  global p1 = 30e6  ; horizontal far-field stress
  global p2 = 15e6  ; vertical far-field stress
  global a  = 1     ; tunnel radius
  
  global bm = 3.9e9
  global sm = 2.8e9
  global nu = (3.*bm-2.*sm)/(6.*bm+2.*sm)
end
; =================================================
; Stresses
; =================================================
fish define nastr
    local numrad = 0
    local tab1  = table.get(1)
    local tab2  = table.get(2)
    local tab3  = table.get(3)
    local tab4  = table.get(4)
    table.label(tab1) = 'analytic-sigr'
    table.label(tab2) = 'analytic-sigt'
    table.label(tab3) = '3DEC-sigr'
    table.label(tab4) = '3DEC-sigt'
    global errsr
    global errst
    errsr = 0.0
    errst = 0.0
	
    loop foreach local iz_ block.zone.list
         local mark = 0
         local igp
         loop igp (1,4)
              local gpind = block.zone.gp(iz_,igp)
              if block.gp.pos.z(gpind) < 0.001 then
                 mark = mark + 1
              end_if
         end_loop
         
         local rad = math.sqrt(block.zone.pos.x(iz_)^2 + ...
                     block.zone.pos.z(iz_)^2)
         local theta_ = math.atan2(block.zone.pos.z(iz_),block.zone.pos.x(iz_))
         local o_r = a/rad
         local o_r2 = o_r*o_r
         local o_r4 = o_r2*o_r2

         local sigre = 0.5*(p1+p2)*(1-o_r2)
         sigre = sigre+0.5*(p1-p2)*(1.-4.*o_r2+3.*o_r4)*math.cos(2.0*theta_)

         local sigte = 0.5*(p1+p2)*(1+o_r2)
         sigte = sigte-0.5*(p1-p2)*(1.+3.*o_r4)*math.cos(2.0*theta_)
         
         local stemp1 = 0.5*(block.zone.stress.xx(iz_) + ...
                        block.zone.stress.zz(iz_))
         local stemp2 = 0.5*(block.zone.stress.xx(iz_) - ...
                        block.zone.stress.zz(iz_))
         local stemp3 = block.zone.stress.xz(iz_)*math.sin(2.0*theta_)
         local sigr = -(stemp1 + stemp2*math.cos(2.0*theta_)+stemp3)
         local sigt = -(stemp1 - stemp2*math.cos(2.0*theta_)-stemp3)
 
         if mark > 2
           if rad < 5.0
              numrad = numrad + 1
              table(tab1,rad) = sigre
              table(tab2,rad) = sigte
              table(tab3,rad) = sigr
              table(tab4,rad) = sigt
            end_if
         end_if
         local err = math.abs(sigr - sigre) / p1
         errsr = errsr + err
         err = math.abs(sigt - sigte) / p1
         errst = errst + err
    end_loop
    errsr = errsr * 100. / block.zone.num
    errst = errst * 100. / block.zone.num
end
; =================================================
; Displacements
; =================================================
fish define nadis
    global numrad
    numrad = 0
    local tab5  = table.get(5)
    local tab6  = table.get(6)
    table.label(tab5) = 'analytic-ur'
    table.label(tab6) = '3DEC-ur'
    
    ; solution at edge for error calculation
    local dism = 0.25*((p1+p2)+(p1-p2)*(4.*(1.-nu)-1.0))/sm

    global errd = 0.0
    local count_ = 0

    loop foreach local igp_ block.gp.list
         count_ = count_ + 1
         local mark = 0
         if block.gp.pos.z(igp_) < 0.001 then
            if block.gp.pos.y(igp_) < 0.001 then
              mark = 1
            end_if
         end_if
         local rad = math.sqrt(block.gp.pos.x(igp_)^2 + block.gp.pos.z(igp_)^2)
         local theta_ = math.atan2(block.gp.pos.z(igp_),block.gp.pos.x(igp_))
         local o_r = a/rad
         local dise = (p1+p2)+(p1-p2)*(4.*(1.-nu)-o_r*o_r)*math.cos(2.0*theta_)
         dise = 0.25*dise*o_r*a/sm

         local dis = math.sqrt(block.gp.disp.x(igp_)^2 + ...
                     block.gp.disp.z(igp_)^2)
         local err = math.abs(dis - dise)
         errd = errd + err
         if mark = 1 then
           if rad < 5.0
              numrad = numrad + 1
              table(tab5,rad) = 100*dise
              table(tab6,rad) = 100*dis
            end_if
         end_if
    end_loop
    errd = errd * 100. / (dism*count_)
end
;
[props]
[nastr]
[nadis]
;
fish list [numrad]
fish list [errsr]
fish list [errst]
fish list [errd]
fish automatic-create on
; eof

Endnote

[1]

This example is listed under the present document title in the i Examples dialog use the menu command Help -> Examples… to access.