Simulating Square Permanent Magnets
Problem Statement
Note
The project file for this example may be viewed/run in PFC.[1] The data files used are shown at the end of this example.
This verification problem compares the analytic solution for the attractive forces/moments for square ferromagnets, derived by [Akoun1984], with those produced by the Linear Dipole Model contact model. This test is based on the configuration reported in [Thomaszewski2008]. That article compares only the attractive force as a function of separation in the direction of common faces of the magnets. In the present example, the square magnets are separated with displacements not parallel with a common face and all components of the force and moment are compared.
Clumps with Many Pebbles
A square clump with a 1 cm side is created with various numbers of pebbles. The clumps have uniform magnetic induction of 1 Tesla. The corresponding magnetic moment is set for each pebble accounting for the total number of pebbles. Each pebble must interact with each other pebble of the other clump. The side lengths are 1, 3, and 6 pebbles, resulting in 1, 27, and 216 pebbles per clump and 1, 729, and 46,656 contacts. Consequently, the computational time is dramatically higher for the 216 pebble case.
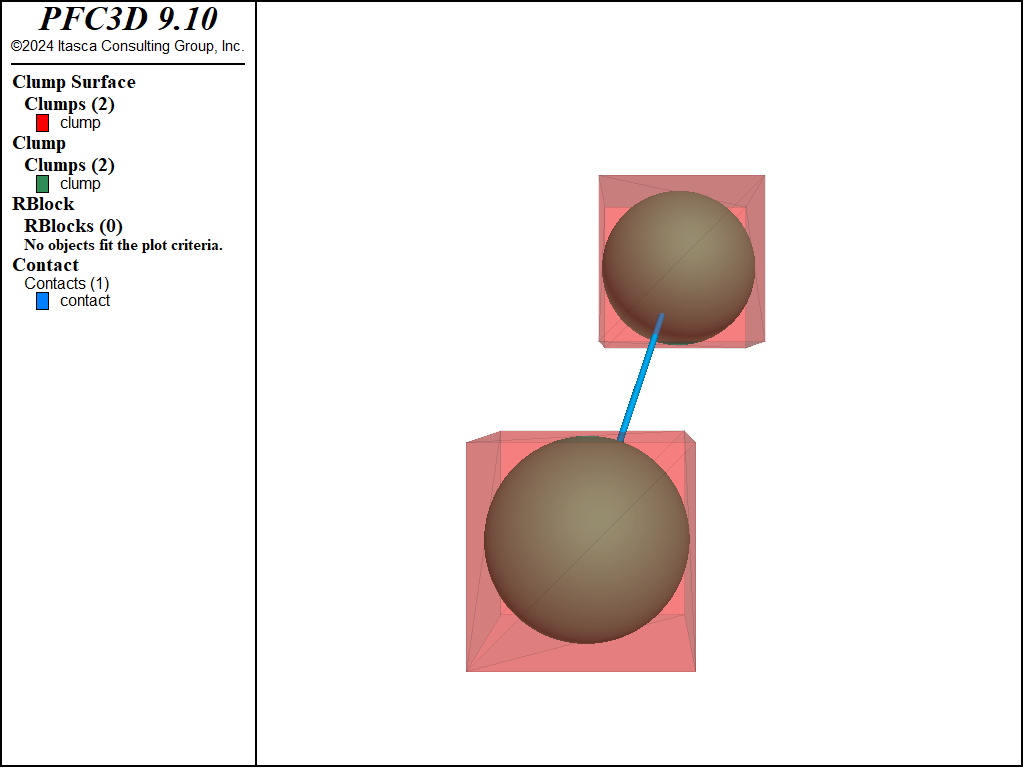
Figure 1: Single pebble square magnets with the resulting contact at the end of the simulation.
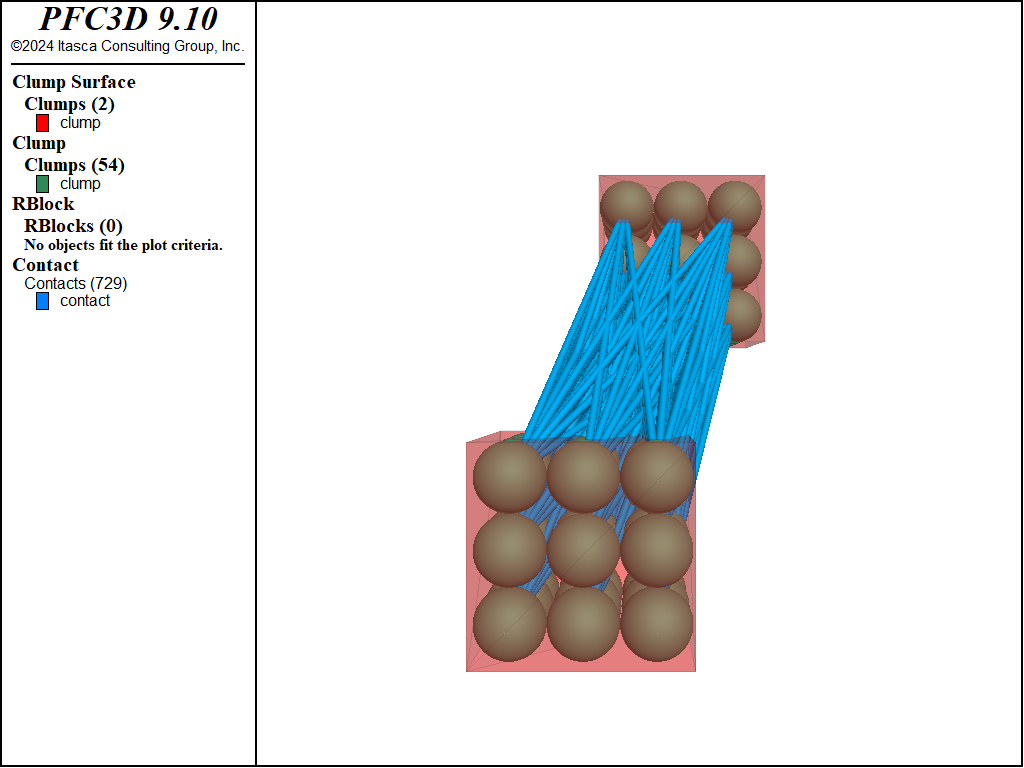
Figure 2: 27 pebble square magnets with the resulting contacts at the end of the simulation.

Figure 3: 216 pebble square magnets with the resulting contacts at the end of the simulation.
In order for the simulation to proceed, orientation tracking is enabled and the dipole_mo property is set per pebble. The timestep is fixed as are the clump velocities and spins. The top clump displaces unequally in the positive \(x\)-, \(y\)- and \(z\)-directions.
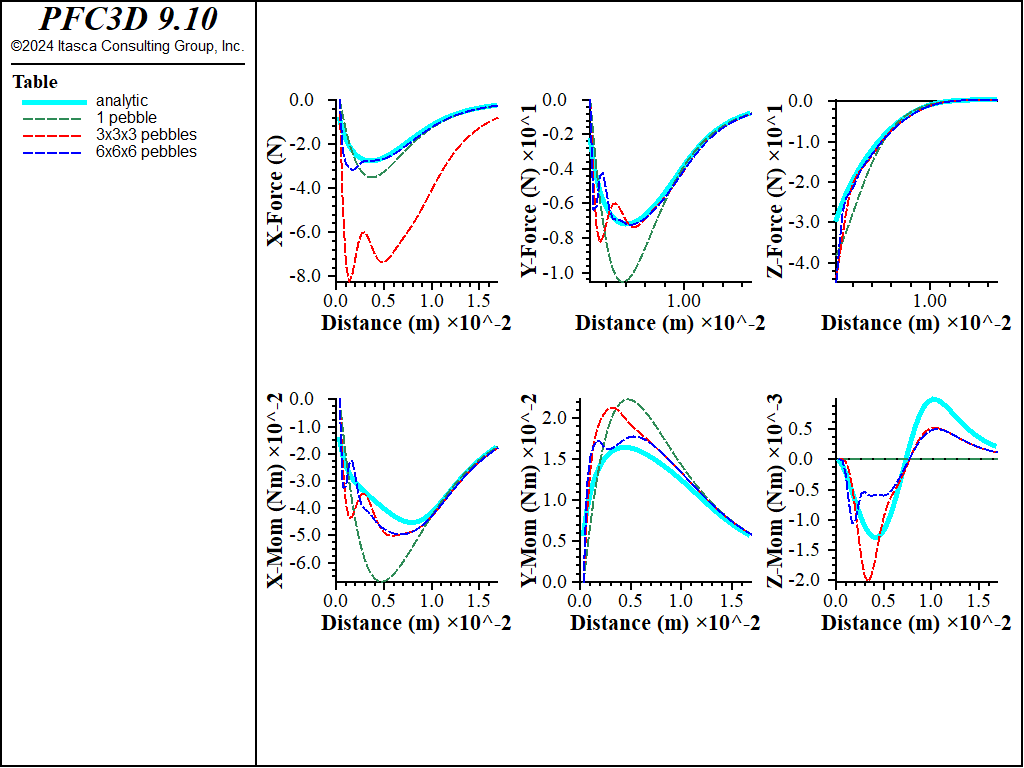
Figure 4: Histories of various attractive force/moment components.
As shown in the figure above, the response is generally closer to the analytic response as the number of pebbles increases. The dipole response (i.e., single pebble case) may be adequate for many applications composed of large numbers of magnetic particles.
Rigid Blocks using FISH Lists
In addition to the strategy of having multiple clump pebbles acting as dipoles with long range interactions, the dipole_pos property stored as a piece property can be used to specify multiple dipole positions inside a single piece as a FISH list. These locations are centered on the piece centroid and are updated based on the current piece orientation and position. Each dipole can also have a different initial dipole moment using the dipole_mo property stored as a piece property, though this is not necessary in this specific example. There is a substantial performance benefit to this approach if many dipoles are required. For instance, cycling the six pebble clump example is an order of magnitude slower than the rigid block example and produces the same response (below).
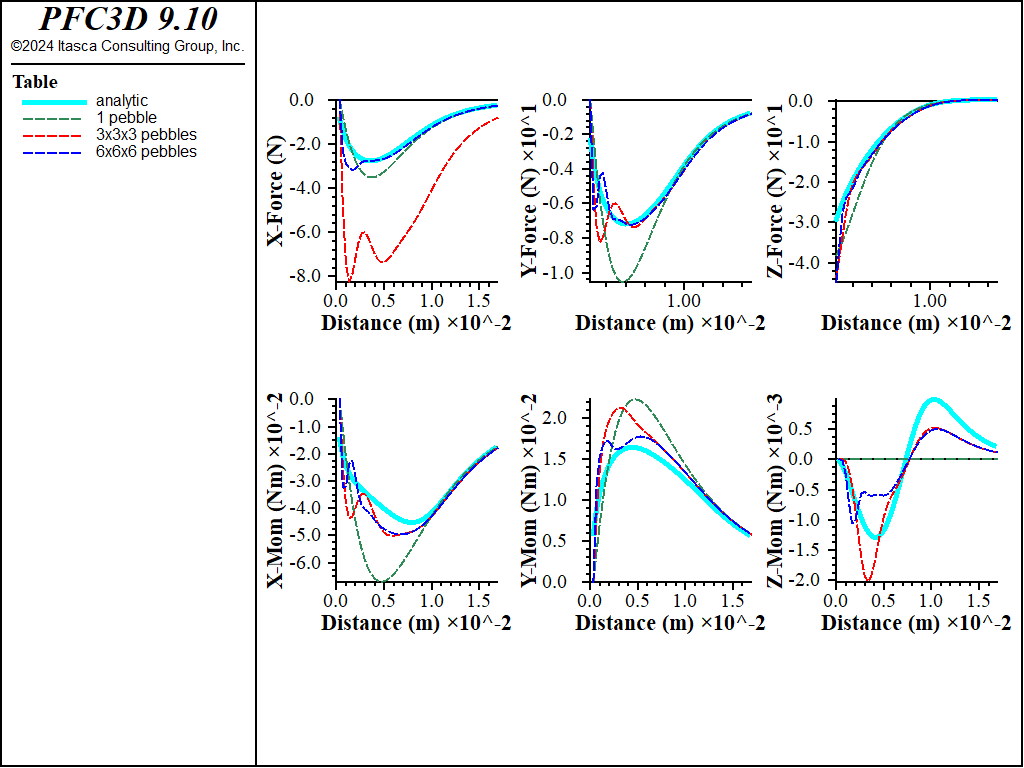
Figure 5: Histories of various attractive force/moment components using rigid blocks and FISH lists for the properties.
Data Files
squareMagnet.dat (3D)
; Compare the analytic solution for a square magnet with the
; response for increasing number of pebbles .
model new
; Make tables to store analytic values.
table 'forcex'
table 'forcey'
table 'forcez'
table 'torquex'
table 'torquey'
table 'torquez'
; Analytic response from Akoun and Yonnet 1984.
fish define analytic
; displacement per timestep
dd = vector(1.0e-4,3.0e-4,1.0e-4)
; number of points for the computation
num = 50
local tfx = table.find('forcex')
local tfy = table.find('forcey')
local tfz = table.find('forcez')
local ttx = table.find('torquex')
local tty = table.find('torquey')
local ttz = table.find('torquez')
local ca = 0.5/100.0
local cb = ca
local cc = ca
local a = ca
local b = ca
local c = ca
pos = vector(0.0,0.0,1.0/100.0)
array U(2,2)
array V(2,2)
array W(2,2)
loop local outs(1,num)
local np = pos + dd * outs
loop local i (0,1)
loop local j (0,1)
U(i+1,j+1) = np->x + (-1)^j*ca-(-1)^i*a
V(i+1,j+1) = np->y + (-1)^j*cb-(-1)^i*b
W(i+1,j+1) = np->z + (-1)^j*cc-(-1)^i*c
endloop
endloop
local x = 0.0
local y = 0.0
local z = 0.0
local tx = 0.0
local ty = 0.0
local tz = 0.0
loop i (0,1)
local ii = i+1
loop j (0,1)
local jj = j+1
loop local k (0,1)
local kk = k+1
loop local l (0,1)
local ll = l+1
loop local p (0,1)
local pp = p+1
loop local q (0,1)
local qq = q+1
local frnt = ((-1)^(i+k+p+j+l+q)) ...
/4.0/math.pi/(4.0*math.pi*1.0e-7)
local UU = U(ii,jj)
local VV = V(kk,ll)
local WW = W(pp,qq)
local r = math.sqrt(UU^2+VV^2+WW^2)
local xcont = (VV*VV-WW*WW)*0.5 ...
* math.ln(r-UU)+UU*VV*math.ln(r-VV) ...
+VV*WW*math.atan(UU*VV/WW/r)+0.5*UU*r
local ycont = (UU*UU-WW*WW)*0.5 ...
*math.ln(r-VV)+UU*VV*math.ln(r-UU) ...
+UU*WW*math.atan(UU*VV/WW/r)+0.5*VV*r;
local zcont = -UU*WW*math.ln(r-UU) ...
-VV*WW*math.ln(r-VV)+UU*VV ...
*math.atan(UU*VV/WW/r)-WW*r;
x = x + frnt*xcont;
y = y + frnt*ycont;
z = z + frnt*zcont;
tx = tx + (-1)*frnt*(ycont ...
*(cc*(-1)^q-WW*0.5)-zcont ...
*(cb*(-1)^l-VV*0.5))
ty = ty + (-1)*frnt*(zcont ...
*(ca*(-1)^j-UU*0.5)-xcont ...
*(cc*(-1)^q-WW*0.5))
tz = tz + (-1)*frnt*(xcont ...
*(cb*(-1)^l-VV*0.5)-ycont ...
*(ca*(-1)^j-UU*0.5));
endloop
endloop
endloop
endloop
endloop
endloop
table(tfx,math.mag(dd*outs)) = x
table(tfy,math.mag(dd*outs)) = y
table(tfz,math.mag(dd*outs)) = z
local mp = np / 2.0
local tt = math.cross(np-mp,vector(x,y,z))
table(ttx,math.mag(dd*outs)) = tx - comp.x(tt)
table(tty,math.mag(dd*outs)) = ty - comp.y(tt)
table(ttz,math.mag(dd*outs)) = tz - comp.z(tt)
endloop
end
[analytic]
model domain extent -1 1
; Turn on orientation tracking.
model orientation-tracking on
; Create a 1 cm square.
geometry set 'square'
geometry generate box -0.005 0.005 -0.005 0.005 -0.005 0.005
; Create a clump template with one pebble
clump template create name 'piecet' geometry 'square' ...
calculate-surface pebbles 1 .005 (0,0,0)
; FISH to create a clump template with various numbers of pebbles.
fish define makeTemplate(num)
local name = 'piece' + string(num)
local clt = clump.template.find('piecet')
local nt = clump.template.clone(clt,name)
loop foreach local peb clump.template.pebblelist(nt)
local p = clump.template.deletepebble(nt,peb)
endloop
local dt = 0.01 / num
local fac = num*num*num
loc = vector(-0.005-dt/2.0,-0.005-dt/2.0,-0.005-dt/2.0)
local oloc = loc
loop local i(1,num)
comp.x(loc) = comp.x(loc) + dt
comp.y(loc) = comp.y(oloc)
loop local j(1,num)
comp.y(loc) = comp.y(loc) + dt
comp.z(loc) = comp.z(oloc)
loop local k(1,num)
comp.z(loc) = comp.z(loc) + dt
p = clump.template.addpebble(nt,dt/2.0,loc)
clump.pebble.prop(p,'dipole_mo') = ...
vector(0.0,0.0,math.sqrt(2.0e-7/math.pi)/fac)
endloop
endloop
endloop
end
; Fix the timestep to 1.
model mechanical timestep fix 1
; Set the dipole model and the distance for activity.
contact cmat default model lineardipole ...
property dipole_d 0.05
; The proximity controls the distance for contact creation.
contact cmat proximity 0.05
; Set to large strain.
model large-strain on
; FISH to run a test.
fish define doTest(id)
makeTemplate(id)
pname = 'piece' + string(id)
command
clump delete
clump replicate name [pname] id 1
clump replicate name [pname] position [pos] id 2
clump fix velocity spin
endcommand
local tfx = table.get(pname + 'forcex')
local tfy = table.get(pname + 'forcey')
local tfz = table.get(pname + 'forcez')
local ttx = table.get(pname + 'torquex')
local tty = table.get(pname + 'torquey')
local ttz = table.get(pname + 'torquez')
local cp = clump.find(2)
loop local i(1,num+1)
command
model cycle 1
endcommand
local f = clump.force.unbal(cp,3)
local np = pos + dd*i;
table(tfx,math.mag(np-pos)) = clump.force.unbal(cp,1)
table(tfz,math.mag(np-pos)) = clump.force.unbal(cp,3)
table(tfy,math.mag(np-pos)) = clump.force.unbal(cp,2)
table(ttx,math.mag(np-pos)) = clump.moment.unbal(cp,1)
table(tty,math.mag(np-pos)) = clump.moment.unbal(cp,2)
table(ttz,math.mag(np-pos)) = clump.moment.unbal(cp,3)
clump.pos(cp) = np
endloop
end
[doTest(1)]
plot 'geometry' export bitmap filename "pebble1.png"
[doTest(3)]
plot 'geometry' export bitmap filename "pebble3.png"
[t = time.clock]
[doTest(6)]
[io.out("It took "+string((time.clock()-t)/100.)+" to do with 6x6x6 pebbles.")]
plot 'geometry' export bitmap filename "pebble6.png"
plot 'histories' export bitmap filename "histories.png"
squareMagnetRBlock.dat (3D)
; Compare the analytic solution for a square magnet with the
; response for increasing number of pebbles .
model new
; Make tables to store analytic values.
table 'forcex'
table 'forcey'
table 'forcez'
table 'torquex'
table 'torquey'
table 'torquez'
; Analytic response from Akoun and Yonnet 1984.
fish define analytic
; displacement per timestep
dd = vector(1.0e-4,3.0e-4,1.0e-4)
; number of points for the computation
num = 50
local tfx = table.find('forcex')
local tfy = table.find('forcey')
local tfz = table.find('forcez')
local ttx = table.find('torquex')
local tty = table.find('torquey')
local ttz = table.find('torquez')
local ca = 0.5/100.0
local cb = ca
local cc = ca
local a = ca
local b = ca
local c = ca
pos = vector(0.0,0.0,1.0/100.0)
array U(2,2)
array V(2,2)
array W(2,2)
loop local outs(1,num)
local np = pos + dd * outs
loop local i (0,1)
loop local j (0,1)
U(i+1,j+1) = np->x + (-1)^j*ca-(-1)^i*a
V(i+1,j+1) = np->y + (-1)^j*cb-(-1)^i*b
W(i+1,j+1) = np->z + (-1)^j*cc-(-1)^i*c
endloop
endloop
local x = 0.0
local y = 0.0
local z = 0.0
local tx = 0.0
local ty = 0.0
local tz = 0.0
loop i (0,1)
local ii = i+1
loop j (0,1)
local jj = j+1
loop local k (0,1)
local kk = k+1
loop local l (0,1)
local ll = l+1
loop local p (0,1)
local pp = p+1
loop local q (0,1)
local qq = q+1
local frnt = ((-1)^(i+k+p+j+l+q)) ...
/4.0/math.pi/(4.0*math.pi*1.0e-7)
local UU = U(ii,jj)
local VV = V(kk,ll)
local WW = W(pp,qq)
local r = math.sqrt(UU^2+VV^2+WW^2)
local xcont = (VV*VV-WW*WW)*0.5 ...
*math.ln(r-UU)+UU*VV*math.ln(r-VV) ...
+VV*WW*math.atan(UU*VV/WW/r)+0.5*UU*r
local ycont = (UU*UU-WW*WW)*0.5 ...
*math.ln(r-VV)+UU*VV*math.ln(r-UU) ...
+UU*WW*math.atan(UU*VV/WW/r)+0.5*VV*r;
local zcont = -UU*WW*math.ln(r-UU) ...
-VV*WW*math.ln(r-VV)+UU*VV ...
*math.atan(UU*VV/WW/r)-WW*r;
x = x + frnt*xcont;
y = y + frnt*ycont;
z = z + frnt*zcont;
tx = tx + (-1)*frnt*(ycont ...
*(cc*(-1)^q-WW*0.5)-zcont ...
*(cb*(-1)^l-VV*0.5))
ty = ty + (-1)*frnt*(zcont ...
*(ca*(-1)^j-UU*0.5)-xcont ...
*(cc*(-1)^q-WW*0.5))
tz = tz + (-1)*frnt*(xcont ...
*(cb*(-1)^l-VV*0.5)-ycont ...
*(ca*(-1)^j-UU*0.5));
endloop
endloop
endloop
endloop
endloop
endloop
table(tfx,math.mag(dd*outs)) = x
table(tfy,math.mag(dd*outs)) = y
table(tfz,math.mag(dd*outs)) = z
local mp = np / 2.0
local tt = math.cross(np-mp,vector(x,y,z))
table(ttx,math.mag(dd*outs)) = tx - tt->x
table(tty,math.mag(dd*outs)) = ty - tt->y
table(ttz,math.mag(dd*outs)) = tz - tt->z
endloop
end
[analytic]
model domain extent -1 1
; Turn on orientation tracking.
model orientation-tracking on
; Create a 1 cm square.
rblock template create 'piecet' box -0.005 0.005 -0.005 0.005 -0.005 0.005
;ret
; FISH to create a clump template with various numbers of pebbles.
fish define makeTemplate(num)
local clt = rblock.template.find('piecet')
;loop foreach local peb clump.template.pebblelist(nt)
; local p = clump.template.deletepebble(nt,peb)
;endloop
local dt = 0.01 / num
local fac = num*num*num
rblock.prop(clt,'dipole_mo') = ...
vector(0.0,0.0,math.sqrt(2.0e-7/math.pi)/fac)
loc = vector(-0.005-dt/2.0,-0.005-dt/2.0,-0.005-dt/2.0)
local oloc = loc
local theList = list
loop local i(1,num)
loc->x += dt
loc->y = oloc->y
loop local j(1,num)
loc->y += dt
loc->z = oloc->z
loop local k(1,num)
loc->z += dt
theList = list.append(theList,loc);
endloop
endloop
endloop
rblock.prop(clt,'dipole_pos') = ...
theList
end
; Fix the timestep to 1.
model mechanical timestep fix 1
; Set the dipole model and the distance for activity.
contact cmat default model lineardipole ...
property dipole_d 0.05
; The proximity controls the distance for contact creation.
contact cmat proximity 0.05
; Set to large strain.
model large-strain on
; FISH to run a test.
fish define doTest(id)
makeTemplate(id)
pname = 'piece' + string(id)
command
rblock delete
rblock replicate 'piecet' id 1
rblock replicate 'piecet' position [pos] id 2
rblock fix velocity spin
endcommand
local tfx = table.get(pname + 'forcex')
local tfy = table.get(pname + 'forcey')
local tfz = table.get(pname + 'forcez')
local ttx = table.get(pname + 'torquex')
local tty = table.get(pname + 'torquey')
local ttz = table.get(pname + 'torquez')
local cp = rblock.find(2)
loop local i(1,num+1)
command
model cycle 1
endcommand
local f = rblock.force.unbal(cp,3)
local np = pos + dd*i;
table(tfx,math.mag(np-pos)) = rblock.force.unbal(cp,1)
table(tfz,math.mag(np-pos)) = rblock.force.unbal(cp,3)
table(tfy,math.mag(np-pos)) = rblock.force.unbal(cp,2)
table(ttx,math.mag(np-pos)) = rblock.moment.unbal(cp,1)
table(tty,math.mag(np-pos)) = rblock.moment.unbal(cp,2)
table(ttz,math.mag(np-pos)) = rblock.moment.unbal(cp,3)
rblock.pos(cp) = np
endloop
end
[doTest(1)]
plot 'geometry' export bitmap filename "pebble1RBlock.png"
[doTest(3)]
plot 'geometry' export bitmap filename "pebble3RBlock.png"
[t = time.clock]
[doTest(6)]
[io.out("It took "+string((time.clock()-t)/100.)+" to do with a 6x6x6 list.")]
plot 'geometry' export bitmap filename "pebble6RBlock.png"
plot 'histories' export bitmap filename "historiesRBlock.png"
References
Akoun, G. and J.-P. Yonnet. “3D analytic calculation of the forces exerted between two cuboidal magnets” in IEEE Trans. Magn., 20, pp. 1962-1964, 1984.
Endnote
⇐ Spring Network Contact Model Capabilities | Pull-Test for a Grouted Cable Anchor in a PFC Rigid Block Model ⇒
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Aug 13, 2024 |
