Wharf Subjected to Earthquake Loading (FLAC3D)

Problem Statement

Note

The project file for this example is available to be viewed/run in FLAC3D.[1] The project’s main data files are shown at the end of this example.

This is an illustrative example of a wharf subjected to earthquake loading. The soil profile with three layers (4.5, 6.5 and 11.0 m) is shown in Figure 1. The water table is 2 m below the slope ground. The wharf and its piles are shown in Figure 2 in three-dimension. The slope contains sand that may spread laterally during an earthquake. This lateral spreading could push the piles and potentially compromise the safety of the wharf. However, the piles also have a spinning effect that can reduce the lateral spreading of the slope. This is an example of soil-structure interaction.

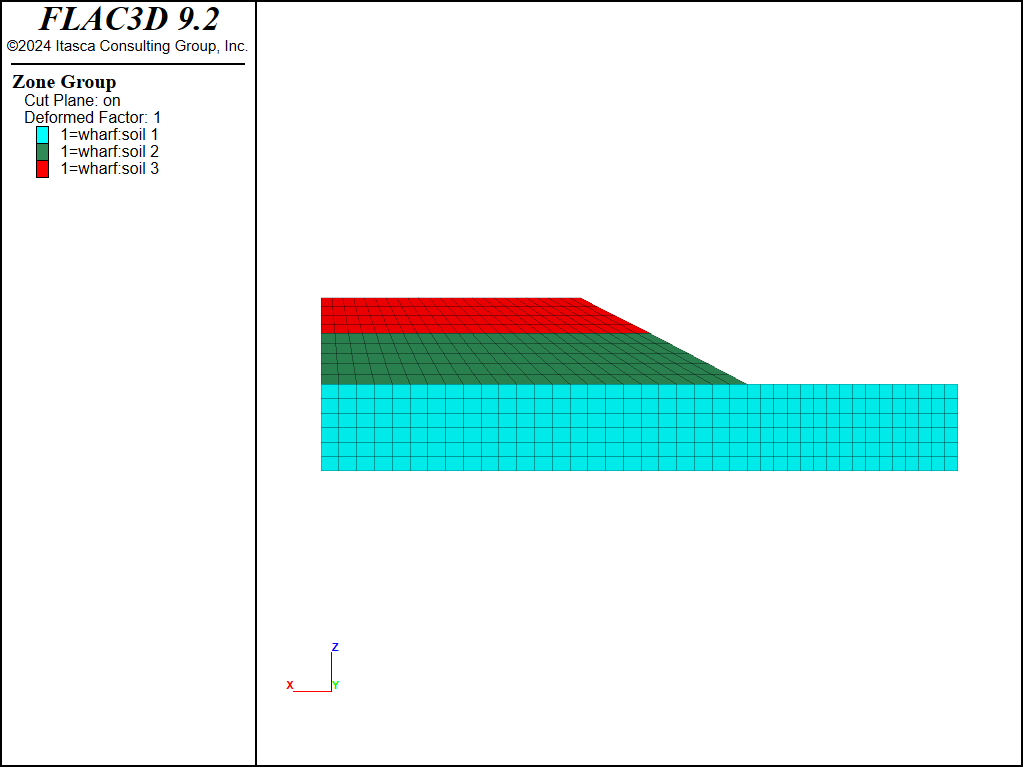
Figure 1: Soil profile.

The liquefiable part of the middle layer is modeled using the P2PSand model (colored by green in Figure 2 and Figure 3) and other soils are modeled using the Mohr-Coulomb model plus hysteretic damping.

Several analysis stages are required:

• setup initial stress and pore-pressure;

• install structures;

• assign P2PSand model; and

• dynamic analysis.

Setup initial stress and pore-pressure

This model requires configures of fluid and dynamic (model configure fluid dynamic. At this stage, both fluid and dynamic are off. This model follows the standard boundary conditions: fixed degrees of freedom at the bottom and roller boundaries on the side surfaces. Take advantage of the command zone face skin, the boundary conditions can be

zone face apply velocity (0,0,0) range group 'bottom'
;
zone cmodel assign mohr-coulomb

At this stage, all soils are assumed Mohr-Coulomb. The soil matrix material properties are list in Table 1.

Table 1: Soil Properties

Soil	Density	Bulk	Shear	Friction	Cohesion
	Mg/m3	kPa	kPa	deg.	kPa
#1	1.7	5.10e5	2.35e5	40	4
#2	1.5	1.36e5	6.30e4	35	2
#3	1.4	1.36e5	6.30e4	30	2

The fluid related material properties are water density \(\rho_f\) = 1e3 \(kg/m^3\), porosity = 0.3. Gridpoint above the water table is set to zero saturation while others are 1 by default. Note that the input density should be dry density since the fluid is configured.

The pore pressures are initialized statically using a gradient. The static water pressure should be applied to the top surfaces below the water table. These can be achieved with two simple commands:

zone gridpoint pore-pressure head 20
zone face apply stress-normal -200 gradient 0 0 10 ... 
        range group 'top' position-z -10.99 20
model fluid active off

The model is cycled to equilibrium by the command:

model solve-static elastic

Install Structures

This stage sets up the wharf structures.

Before installation of structures, the model should be re-initialized to zero displacements and velocities and be cleared of all yield states because any previously calculated displacement/velocity and yield states are solely provide an initial field of stress and pore-pressure for subsequent stages. These operations are performed with the commands:

zone gridpoint initialize velocity (0,0,0)
zone gridpoint initialize displacement (0,0,0)
zone initialize state 0

The platform is modeled by shell elements and the foundations are modeled by pile elements. The thickness of the shell is 0.3 m. The diameter of the piles is 0.6 meter. The structure geometry and properties are summarized in Table 2. The friction between the pile and the soil is assumed to be 30 degrees.

Table 2: Structure Properties

Structure	Density	Young	Poisson	Thickness	Diameter
	Mg/m3	kPa		m	m
Shell	2	2e8	0.2	0.3
Pile	2	2e7	0.2		0.6

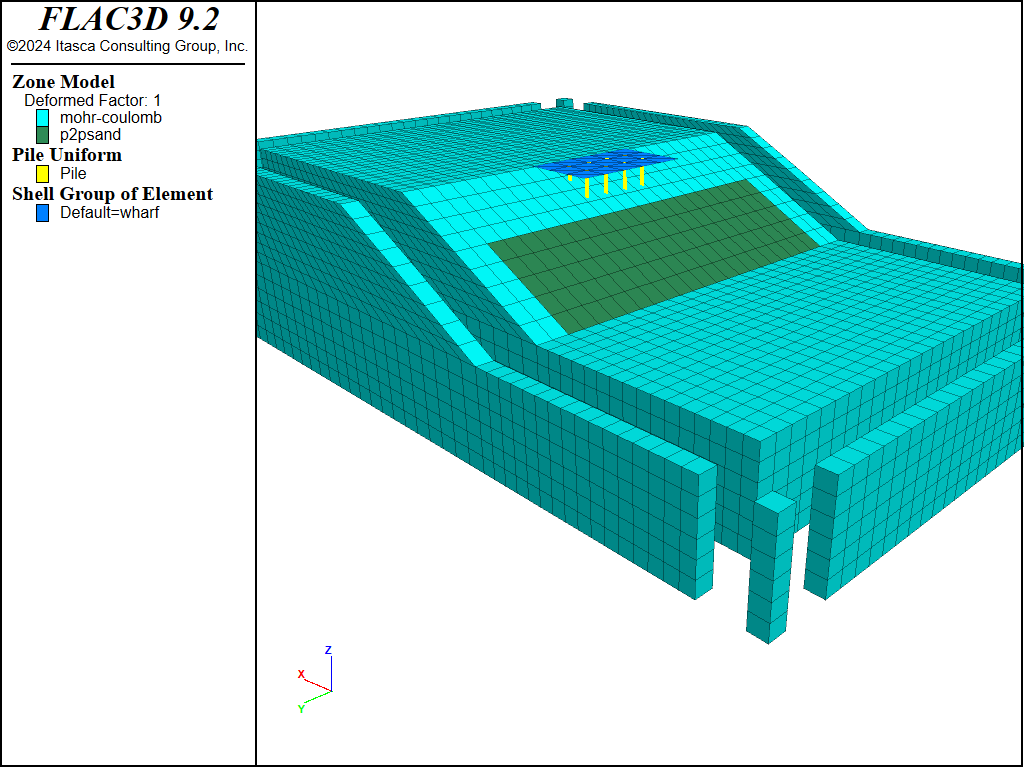
Figure 2: 3D soil profile and schematic of wharf and its piles.

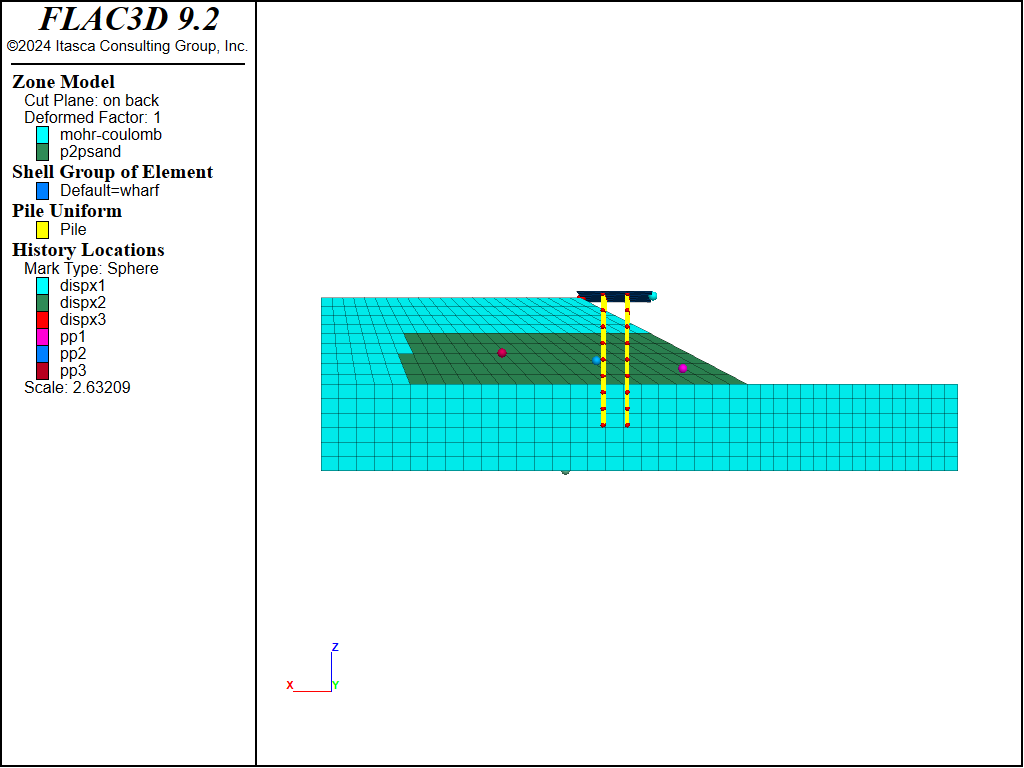
Figure 3: Constitutive models.

To account for the end-bearing effect of the piles, an additional set of links are created at the pile ends. This is necessary because the default pile links are frictional. If a node requires multiple links, the links can be created on a different ‘side’. In this model, the ‘side=2’ designation is used for end-bearing links (grouped under the name ‘End’) between the piles and the soil. The end-bearing links are assumed to be of the norm-yield type.

Note that the link displacement is defined as the target displacement minus the node displacement. The (downward) driving is regarded as the ‘tension’ of the link, while the (upward) pulling is considered the ‘compression’ of the link. Therefore, the yield-compression of the link is set to zero, while the yield-tension is assigned a large value to ensure consistency with the effect of end-bearing. The commands associated with the end-bearing links are:

    perimeter [math.pi*d] coupling-gap-normal off
; Include end-bearing effect
structure link create side=2 target zone group 'End' range position-z 5.9 6.1
structure link attach x=normal-yield y=free z=free range group 'End'
structure link attach rotation-x=free rotation-y=free rotation-z=free range group 'End'

To make sure the pile heads are rigidly linked to the shell, the following command is used

structure shell property density 2 young 2e8 poisson 0.2 ... 

Again, the model is cycled to equilibrium for the installation of the structures.

Assign P2PSand model

The P2PSand model is applied to certain zones within the middle soil layer (colored by green in Figure 2 and Figure 3). To simplify the analysis and demonstration, the internally calibrated material parameters for the P2PSand model are utilized. The primary parameter, relative-density-initial, is set at 0.50 and 0.75 to examine the impact of sand densities on the dynamic behavior of the slope and wharf. The reference pressure is assigned as pressure-reference = 100, as the model’s unit for stress/pressure is in kPa.

Because the P2PSand model is a stress-dependent model, the initial stress will be utilized to determine the initial moduli. A small FISH function is adopted here:

fish operator ini_stress(z, modelname)
    if zone.model(z) == modelname then
        local pp = zone.pp(z)
        zone.prop(z,'stress-xx-initial') = zone.stress.xx(z) + pp
        zone.prop(z,'stress-yy-initial') = zone.stress.yy(z) + pp
        zone.prop(z,'stress-zz-initial') = zone.stress.zz(z) + pp
        zone.prop(z,'stress-xy-initial') = zone.stress.xy(z) 
        zone.prop(z,'stress-yz-initial') = zone.stress.yz(z)
        zone.prop(z,'stress-xz-initial') = zone.stress.xz(z)
    endif
end
[ini_stress(::zone.list, 'p2psand')]

Note that here the keyword operator is used in place of the usual define, declaring it a function to be used with multi-threading. The argument ‘z’ is a zone pointer and ‘modelname’ is a constitutive model name. The command [ini_stress(::zone.list, ‘p2psand’)] runs the FISH function “ini_stress” in a multi-threaded mode.

After assigning the P2PSand model, the model requires another re-initialization of displacement/velocity and yield state to zero. This time, structure nodes require similar re-initialization as well:

structure node initialize displacement (0,0,0)
structure node initialize displacement-rotational (0,0,0)

To this point, all necessary constitutive models and structures with allowable stress, pore-pressure, and structural forces forces are set up. The model is ready for dynamic analysis.

Dynamic Analysis

The dynamic configure needs to be turned on for dynamic analysis. For quicker calculation, the ‘multi-step’ is turned on as well. Because the earthquake can be considered a quick loading, the response of the soil is approximately considered undrained process. The fluid modulus is assigned a non-zero value 2e5 Pa so that the deformation from the soil matrix can cause the change of pore-pressure. Note that a smaller water bulk modulus 2e5 Pa rather than the real water bulk modulus 2e6 Pa is assigned to compromise the effect the free surface of water table (water is not completely confined). The commands are:

zone dynamic multi-step on
zone fluid property fluid-modulus 2e5
zone fluid property pore-pressure-generation on

The base of the model is considered compliant, so the input motion at the base should be the upward motion, or half of the outcrop motion. The input outcrop motion (labeled Nahanni) before scaling is shown in Figure 4:

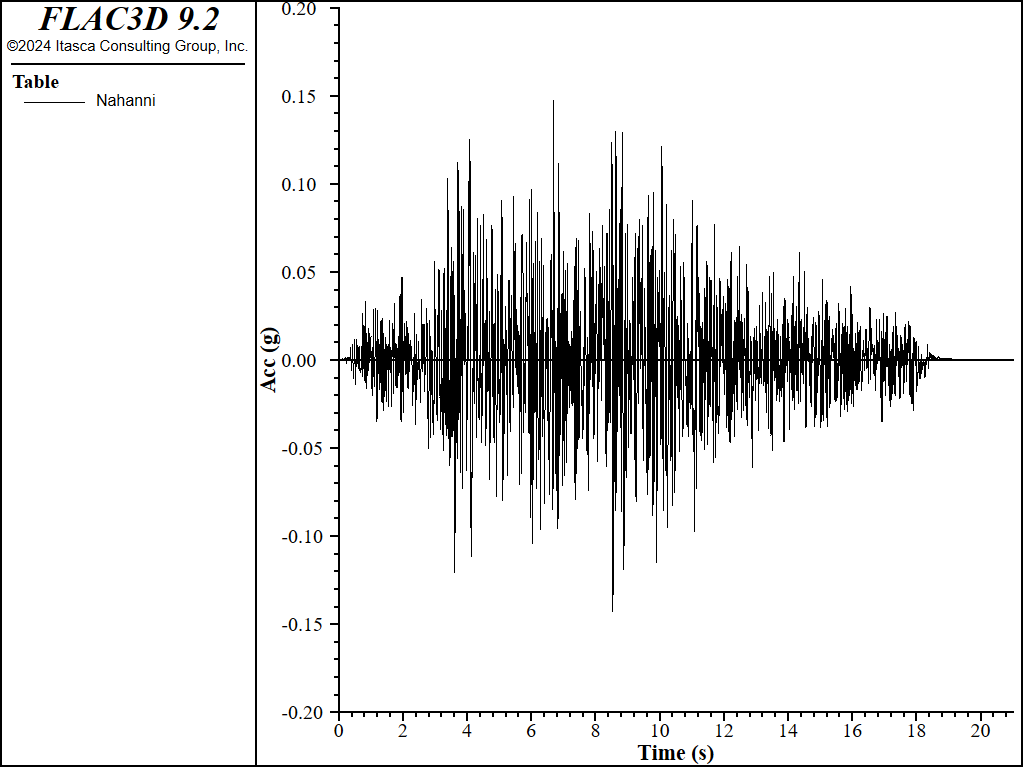
Figure 4: Input acceleration motion before scaling.

In practice, the adopted input motion is usually be scaled to abide by some design codes or guidelines. In this example, a scaling factor of 5 is used so that the maximum acceleration is around 0.75 g.

At the base, quiet boundaries are used to accommodate the compliant base. The input acceleration motion is integrated into a velocity motion and then into a shear stress history. Shear stress can be calculated from velocity by:

\[\tau = -2 \rho C_s v_{s,upward} = - \rho C_s v_{s,crop}\]

where \(\rho\) is density at the base, \(G\) is the shear modulus at the base, and \(v_s\) is the shear wave velocity, and \(C_s = \sqrt{G / \rho}\) is the speed of s-wave propagation at the base.

The commands are

zone gridpoint free velocity
table 'acc' import "Nahanni.acc"
[table.as.list('vel') = table.integrate('acc')]
; since g=10, scaling factor=5
[global mf = -1.8*math.sqrt(2.35e5/1.8)*10*5.0] 
zone face apply stress-dip [mf] table 'vel' range group 'bottom'
zone face apply stress-strike 0.0 range group 'bottom'
zone face apply stress-normal 0.0 range group 'bottom'
zone face apply quiet range group 'bottom'

For zones that use the Mohr-Coulomb model, hysteretic damping is incorporated to account for the \(G/G_{max}\) effect. In contrast, zones that use the P2PSand model have an intrinsic energy dissipation in their constitutive relation, so additional energy dissipation is not strictly necessary. However, a small amount of Rayleigh damping is added to zones in order to reduce high-frequency noise. Since the Rayleigh damping is very small, the dynamic timestep is rarely affected.

For structures, the situation is different as the inclusion of Rayleigh damping can significantly reduce the timestep. Therefore, this model uses Maxwell damping with a target damping ratio of 5% for structures (see Maxwell Damping):

zone dynamic damping hysteretic hardin 0.2 range cmodel 'mohr-coulomb'
zone dynamic damping rayleigh 0.0015 1.0 
structure dynamic damping maxwell 0.0385 0.5 0.0335 3.5 0.052 25.0

Free-field boundary is then applied following the basic the guideline for dynamic analysis:

zone dynamic free-field on

The results for sand \(D_r\) = 0.50 (50%) are plotted in Figure 5 to Figure 7. Figure 5 plots pore-pressure histories at selected points (35,25,13), (46,25,14) and (58,25,15). Apparent excess pore-pressure builds-up are observed. Figure Figure #wharf-ss-dr50 plots the contour of the maximum shear strain. Figure 7 plots the X-displacement histories of platform, slope top and the base. Interestingly, the lateral displacement of the platform is less than that of the slope, which is a common effect of soil-structure interaction. Specifically, the lateral spreading of the soil pushes the pile foundation, while the pile foundation reinforces the stability of the slope to some extent.

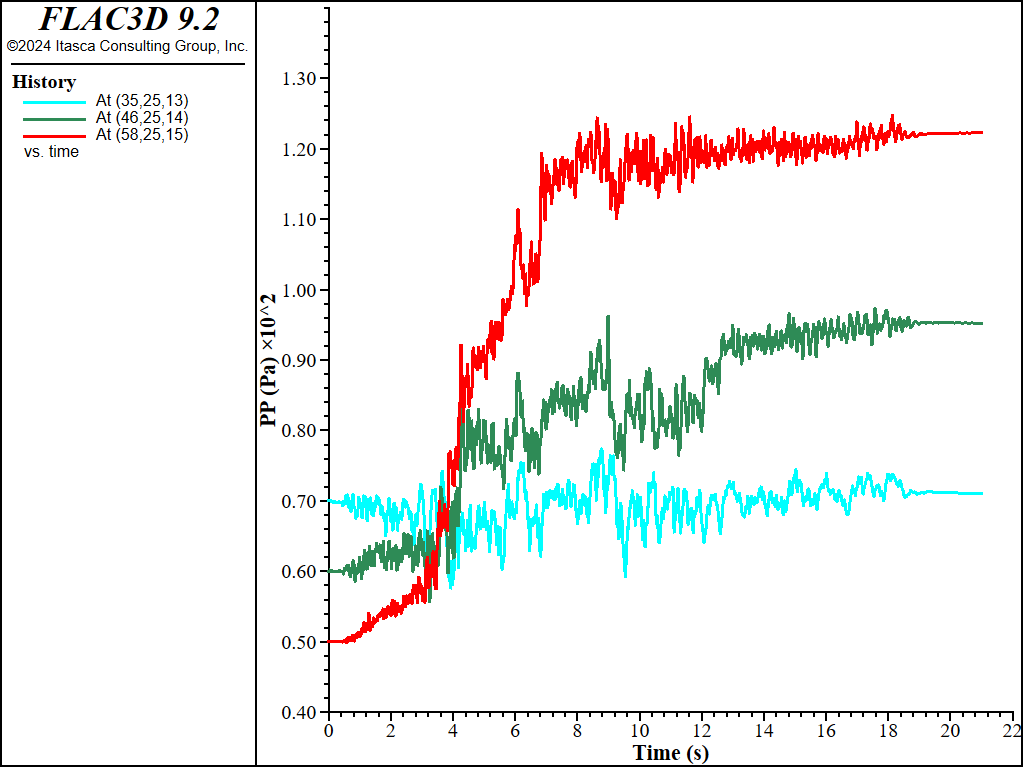
Figure 5: Pore pressure histories for sand Dr = 50%.

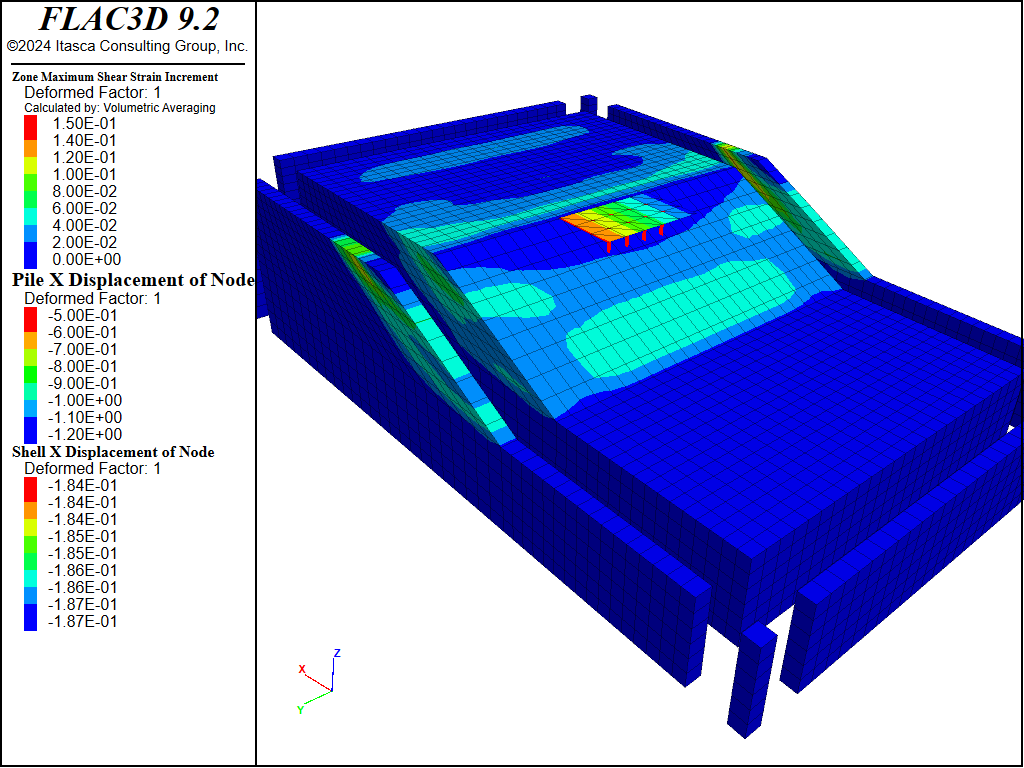
Figure 6: Contour of maximum shear strain for sand Dr = 50%.

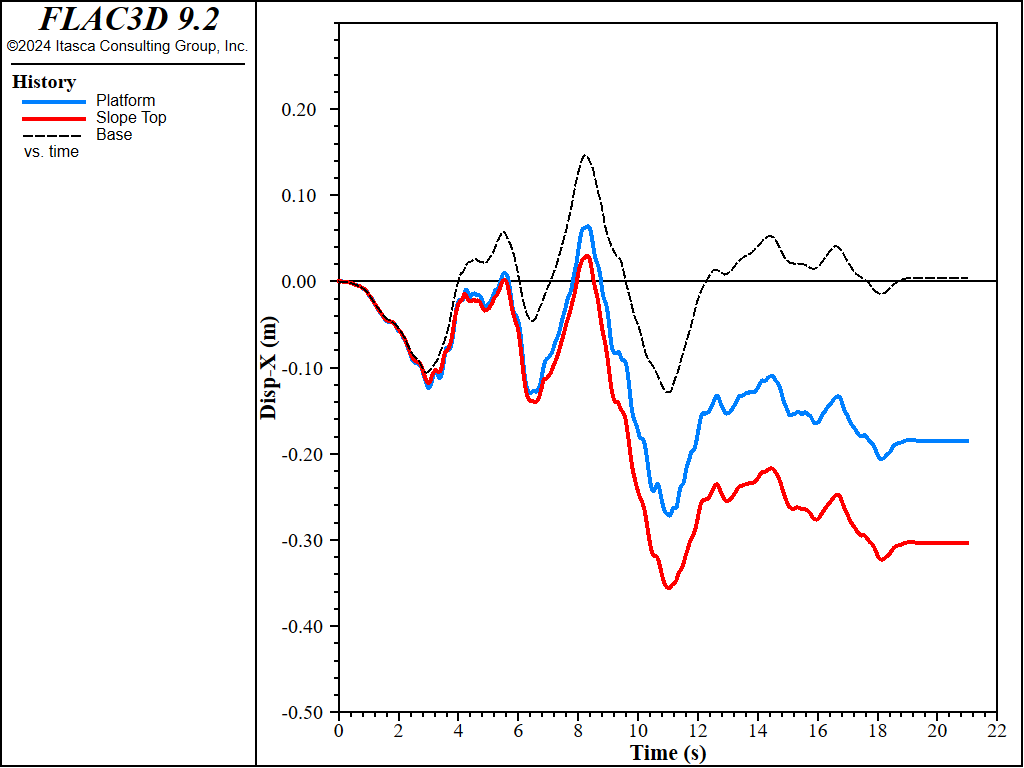
Figure 7: \(x\)-Displacement histories for sand Dr = 50%.

Similar results for sand \(D_r\) = 0.75 (75%) are plotted in Figure 8 to Figure 10. Excess pore-pressure builds-up are observed in Figure 8. Lateral displacements of platform and slope shown in Figure 10 are less than those in Figure 7 which is apparently due to the sand in Figure 10 being denser.

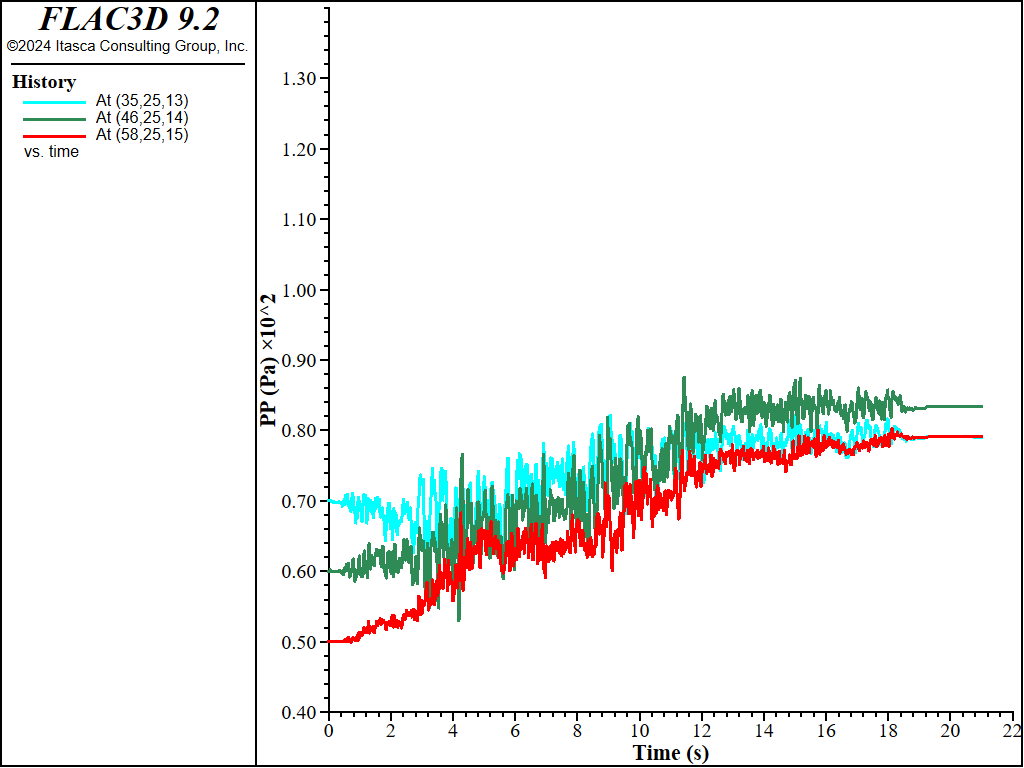
Figure 8: Pore pressure histories for sand Dr = 75%.

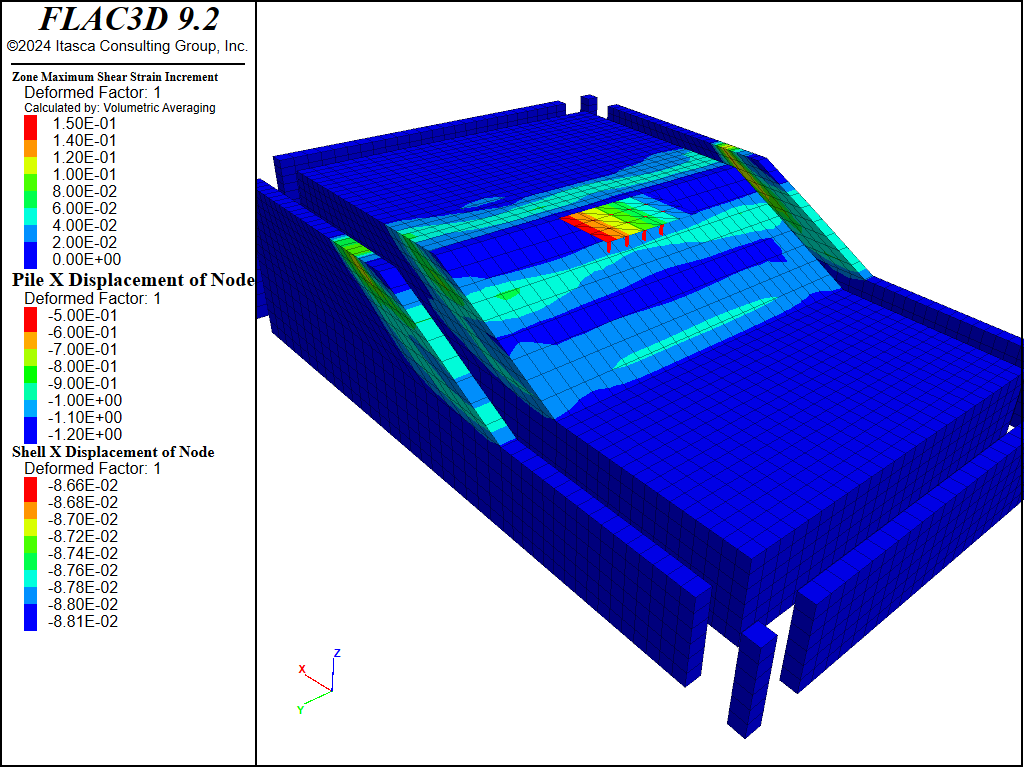
Figure 9: Contour of maximum shear strain for sand Dr = 75%.

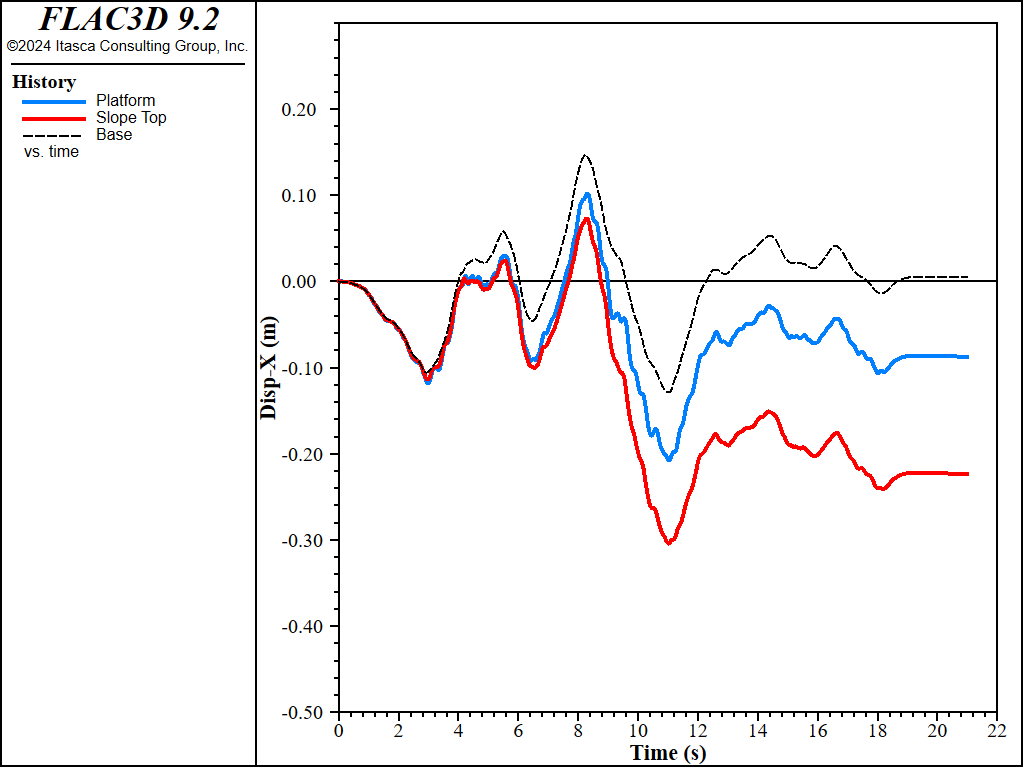
Figure 10: \(x\)-Displacement histories for sand Dr = 75%.

break

Data Files

wharf-ini.dat

model new
model configure dynamic
model large-strain off
model gravity 10
;
zone import 'grid.flac3d'
zone face skin
;
zone face apply velocity-x 0 range union group 'west' group 'east'
zone face apply velocity-y 0 range union group 'north' group 'south'
zone face apply velocity (0,0,0) range group 'bottom'
;
zone cmodel assign mohr-coulomb
zone property  density=1.8 bulk=5.10e5 shear=2.35e5 ... 
          cohesion=4 friction=40.0 range group 'wharf:soil 1'
zone property  density=1.6 bulk=1.36e5 shear=6.30e4 ... 
          cohesion=2 friction=35.0 range group 'wharf:soil 2'
zone property  density=1.5 bulk=1.36e5 shear=6.30e4 ... 
          cohesion=2 friction=30.0 range group 'wharf:soil 3'
;
model configure fluid-flow
zone fluid-density 1.0
zone fluid unsaturated cutoff 0
zone fluid property porosity 0.3 
zone fluid property pore-pressure-generation on
zone gridpoint initialize saturation 0 range position-z 20 100
zone gridpoint pore-pressure head 20
zone face apply stress-normal -200 gradient 0 0 10 ... 
        range group 'top' position-z -10.99 20
model fluid active off
;
model solve-static elastic
;
zone gridpoint initialize velocity (0,0,0)
zone gridpoint initialize displacement (0,0,0)
zone initialize state 0
;
program warning off
structure pile create by-line 42 20.5 6 42 20.5 22.1 segments 8 id 1
structure pile create by-line 45 20.5 6 45 20.5 22.1 segments 8 id 2
structure pile create by-line 42 23.5 6 42 23.5 22.1 segments 8 id 3
structure pile create by-line 45 23.5 6 45 23.5 22.1 segments 8 id 4
structure pile create by-line 42 26.5 6 42 26.5 22.1 segments 8 id 5
structure pile create by-line 45 26.5 6 45 26.5 22.1 segments 8 id 6
structure pile create by-line 42 29.5 6 42 29.5 22.1 segments 8 id 7
structure pile create by-line 45 29.5 6 45 29.5 22.1 segments 8 id 8
program warning on
;
[global d = 0.6]
structure pile property density 2 young 2e7 poisson 0.2 ... 
    cross-sectional-area [math.pi*d^2/4] ... 
    torsion-constant [math.pi*d^4/32] ... 
    moi-y [math.pi*d^4/64] moi-z [math.pi*d^4/64] ... 
    coupling-stiffness-shear 1e5 coupling-cohesion-shear 0 ... 
    coupling-friction-shear 30 coupling-stiffness-normal 1e5 ... 
    coupling-cohesion-normal 0 coupling-friction-normal 30 ... 
    perimeter [math.pi*d] coupling-gap-normal off
; Include end-bearing effect
structure link create side=2 target zone group 'End' range position-z 5.9 6.1
structure link attach x=normal-yield y=free z=free range group 'End'
structure link attach rotation-x=free rotation-y=free rotation-z=free range group 'End'
structure link property x area=[math.pi*d^4/64] stiffness=1e6 ...
       yield-compression=0 yield-tension=1e20 range group 'End'
;
zone create brick size 3 5 1 point 0 39 17.5 21.1 point 1 48 17.5 21.1 ...
    point 2 39 32.5 21.1 point 3 39 17.5 22.1 group 'wharfdeck'
structure shell create by-zone-face id 9 ... 
    range position-x 39 48 position-y 17.5 32.5 position-z 22.0 22.2
structure shell group 'wharf'
zone delete range group 'wharfdeck'
;
structure shell cmodel assign elastic
structure shell property density 2 young 2e8 poisson 0.2 ... 
    thickness 0.3 range id 9
structure node join range group 'wharf'
;
model solve-static
model save 'static'

wharf-p2p-dr75.dat

model restore 'static'
;
zone cmodel assign p2psand range group 'wharf:soil 2' ...
    position-y 5 45 position-x 0 70
zone property relative-density-initial 0.75 pressure-reference 100 ... 
    friction-critical 35.0 range cmodel 'p2psand' 
;
fish operator ini_stress(z, modelname)
    if zone.model(z) == modelname then
        local pp = zone.pp(z)
        zone.prop(z,'stress-xx-initial') = zone.stress.xx(z) + pp
        zone.prop(z,'stress-yy-initial') = zone.stress.yy(z) + pp
        zone.prop(z,'stress-zz-initial') = zone.stress.zz(z) + pp
        zone.prop(z,'stress-xy-initial') = zone.stress.xy(z) 
        zone.prop(z,'stress-yz-initial') = zone.stress.yz(z)
        zone.prop(z,'stress-xz-initial') = zone.stress.xz(z)
    endif
end
[ini_stress(::zone.list, 'p2psand')]
;
model solve-static
;
zone gridpoint initialize displacement (0,0,0)
zone gridpoint initialize velocity (0,0,0)
zone initialize state 0
structure node initialize displacement (0,0,0)
structure node initialize displacement-rotational (0,0,0)
;
zone dynamic multi-step on
zone fluid property fluid-modulus 2e5
zone fluid property pore-pressure-generation on
;
zone gridpoint free velocity
table 'acc' import "Nahanni.acc"
[table.as.list('vel') = table.integrate('acc')]
; since g=10, scaling factor=5
[global mf = -1.8*math.sqrt(2.35e5/1.8)*10*5.0] 
zone face apply stress-dip [mf] table 'vel' range group 'bottom'
zone face apply stress-strike 0.0 range group 'bottom'
zone face apply stress-normal 0.0 range group 'bottom'
zone face apply quiet range group 'bottom'
;
zone dynamic damping hysteretic hardin 0.2 range cmodel 'mohr-coulomb'
zone dynamic damping rayleigh 0.0015 1.0 
; target 5% for structure elements (& transferred to deformabale links)
structure dynamic damping maxwell 0.0385 0.5 0.0335 3.5 0.052 25.0
;
zone dynamic free-field on
;
history delete
history interval 10
model history name 'time' dynamic time-total
program call 'excpphist.f3fis'
zone history name 'pp1' pore-pressure source gridpoint position 35 25 13
zone history name 'pp2' pore-pressure source gridpoint position 46 25 14
zone history name 'pp3' pore-pressure source gridpoint position 58 25 15
structure node history name 'dispx1' displacement-x component-id 86
zone history name 'dispx2' displacement-x position 50 24 0
zone history name 'dispx3' displacement-x position 48 24 22
; If expecting output time interval 1e-3 = 10*1e-4
model dynamic timestep maximum 1.0e-4
model solve-dynamic time-total 21
;
history export 'dispx1' vs 'time' table 'disp1'
table 'disp1' export 'disp1-dr75' truncate
;
model save 'wharf_dr75'

Endnote

[1]

This example is listed under the present document title in the i Examples dialog (use the menu command Help -> Examples… to access.