FLAC3D Theory and Background • Constitutive Models

Isotropic Consolidation Test with Double-Yield Model

Note

To view this project in FLAC3D, use the menu command Help ? Examples…. Choose “ConstitutiveModels/ IsotropicCompressionDoubleYield” and select “IsotropicCompressionDoubleYield.f3dprj” to load. The project’s main data file is shown at the end of this example.

To be sure that input parameters are reasonable, a single-element test is performed with FLAC3D, exercising the double-yield model over stress paths similar to those of the physical tests and plotting similar graphs.

As an illustration, the data file exercises the double-yield model for a material that exhibits a response eleven times stiffer upon unloading than upon loading.

Links to equations in other topics need to be rewritten—awkward as is.

The loading tangent modulus \(dp/de\) observed in the physical test was constant and equal to 10 MPa. The slope of unloading increments corresponded to a value \(K_c\) = 110 MPa. To define the volumetric properties of the numerical model, we substitute those values in the equation on \(R\) and find that \(R\) = 10. As can be seen from the the equation on \(dp_c / de^p\) , the hardening curve has a constant slope corresponding to \(dp_c/de^p = h\) = 11 MPa. The hardening table is derived from this result, assuming no over-consolidation.

Note that the input value for maximum bulk modulus, \(K_{max}\), must be higher than \(K_c\) (see the equation on \(dp_c / de^p\)). The input shear modulus controls the ratio of \(G_{max}/K_{max}\). In this example,

\[G_c = G_{max} {K_c \over K_{max}} = \hbox{50.77\ MPa}\]

and the Poisson’s ratio is

\[\nu = {{3K_c - 2G_c} \over {2(3K_c + G_c)}} = 0.3\]

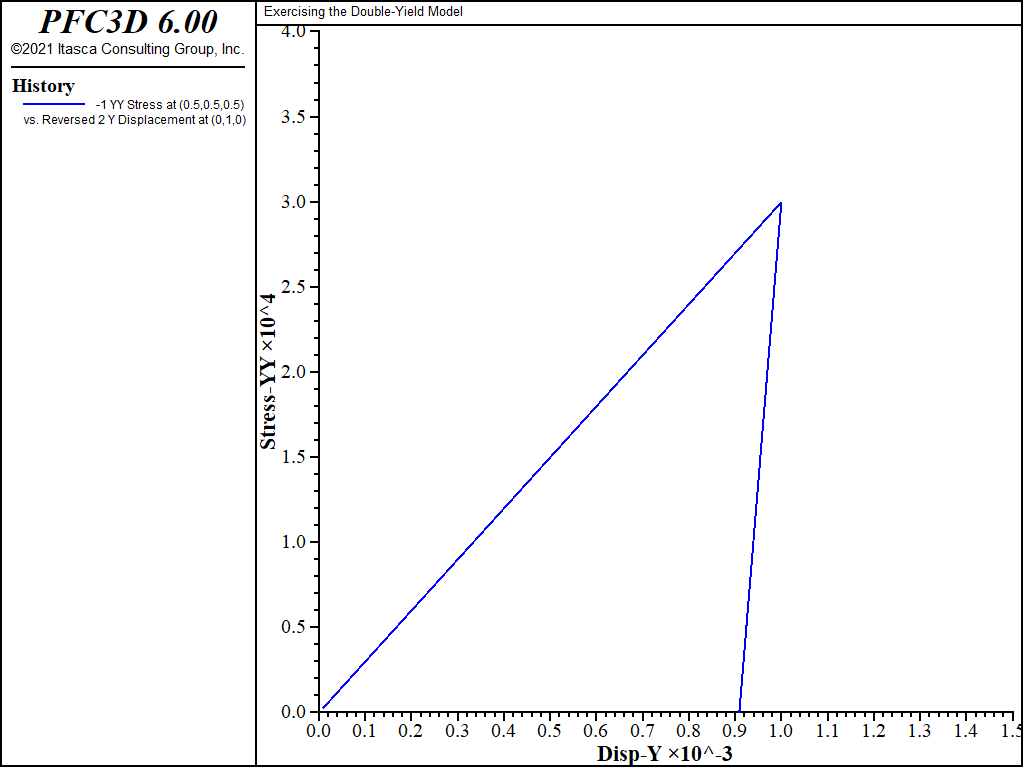
Results of the numerical test are presented in the plot of minus vertical stress versus minus vertical strain in Figure 1. The loading slope is 10 MPa, and the unloading slope is eleven times stiffer, as expected.

Figure 1: Single-element test in which unloading is eleven times stiffer than loading.

The maximum elastic moduli \(K_{max}\) and \(G_{max}\) should be estimated for the maximum pressure likely to be produced in the model. They should not be set larger than this because FLAC3D does mass scaling (for a stable timestep) on the basis of the moduli; setting them too high will give rise to sluggish response (e.g., the model may be slow to converge to a steady-state solution). The elastic moduli also act as a limit on plastic moduli.

If a material to be modeled has experienced some initial compaction (i.e., it is over-consolidated), then \(p_c\) may be set to this pre-consolidation pressure. In this case, \(e^{p}\) must also be set so that it is consistent with \(p_c\) and the given table (use zone property strain-volumetric-plastic to set \(e^{p}\)).

Data File

; Isotropic Conpression Exercising with the double-yield model
model new
model largestrain off
fish automatic-create off
model title "Exercising the Double-Yield Model"
zone create brick size 1 1 1
zone cmodel assign double-yield
zone property bulk-maximum 1110e6 shear-maximum 507.7e6 table-pressure-cap 1 multiplier 10
zone property density 1000 cohesion 1e10 tension 1e10
table 1 add (0,0) (1,1.1e7)
zone gridpoint fix velocity
zone gridpoint initialize velocity-x -1e-6 range position-x 1
zone gridpoint initialize velocity-y -1e-6 range position-y 1
zone gridpoint initialize velocity-z -1e-6 range position-z 1
zone history stress-yy position (0.5,0.5,0.5)
zone history displacement-y position  0 1 0
model step 1000
zone gridpoint initialize velocity-x -0.1 multiply 
zone gridpoint initialize velocity-y -0.1 multiply 
zone gridpoint initialize velocity-z -0.1 multiply 
model step 1600