clump template command

Syntax

clump template keyword ...

Primary keywords:

Operate on a single clump template. A clump template is a reduced version of a clump composed of pebbles. Additionally, a clump template may hold a surface description that can be used for the calculation of inertial parameters and clump visualization. Clump templates can be created, deleted, imported, and exported. Clump templates are not model components, instead they may be used to create clumps using the clump replicate, clump generate, or clump distribute commands. Clumps that refer to clump templates may be visualized via their surface descriptions.

create keyword ...

Create a clump template. The inertial attributes must be specified upon creation. One can either specify them directly (i.e., specify the volume, inertia, and position) or specify their calculation from the pebble distribution (with the pebcalculate keyword) or from the surface description (with the surfcalculate keyword). The pebbles may be specified directly or automatically via the Bubble Pack algorithm of Taghavi (2011). The clump, and all pebbles, are translated so that the clump centroid coincides with the origin. The original clump position is also retained and can be used for replication.

Note

Clump templates are assumed to have unit density, and the inertia must reflect this condition.

bubblepack keyword ...

Specify the creation of the clump template pebbles via the Bubble Pack algorithm of Taghavi (2011). A {linear faceted in 2D; triangulated surface in 3D} must be specified with the geometry keyword and no pebbles can be directly specified. The surface mesh is refined to provide an optimal facet size (see the refinenum keyword for further details) and an approximation of the medial axis is calculated. The medial axis is represented as a set of {circles in 2D; spheres in 3D} that are nearly tangent with the surface. Prospective pebbles are those {circles in 2D; spheres in 3D} whose closest distance from the pebble center to the surface is greater than the pebble radius divided by frad (frad > 1.0). The remaining pebbles are filtered based on their fratio that is the ratio of the smallest to largest pebble in the clump (0 < fratio < 1) and the distance fdistance that corresponds to an angular measure of smoothness in degrees 0 < fdistance < 180 as defined in Taghavi (2011). The algorithm begins by including the largest sphere. Spheres may be included as pebbles if the ratio of their radii to the largest sphere radii is above fratio. The parameter fdistance describes the “distance” between overlapping pebbles where fdistance = 0 for spheres that just touch at one point (i.e., do not overlap) and fdistance = 180 for spheres that just touch at one point where one sphere is contained within the other (i.e, completely overlap). Thus larger values of fdistance result in more pebbles and a smoother surface representation. If the density of pebbles is not sufficient, one may use the refinenum keyword. The bubblepack keyword cannot be given with the pebbles keyword.

distance fdistance: The distance fdistance that corresponds to an angular measure of smoothness in degrees 0 < fdistance < 180 as defined in Taghavi (2011). The greater fdistance, the smoother the pebble distribution.

pebbles i: Set the maximum number of pebbles created to i. By default no maximum is enforced.

ratio fratio: Ratio of the smallest to largest pebble kept in the clump template with 0 < fratio < 1.

radfactor frad: Radius factor used for consideration as a pebble. Prospective pebbles are those whose closest distance from the pebble center to the surface is greater than the pebble radius divided by frad (frad > 1.0 and frad = 1.05 by default). This parameter controls the degree to which the pebbles adhere to the surface with smaller factors resulting in less pebble overlap with the surface.

refinenum i: Specify the maximum number of {linear in 2D; triangular in 3D} facets used when automatically refining the surface mesh. By default, i = {5,000 in 2D; 10,000 in 3D}. Thus, if the bubblepack results in pebbles that are not sufficiently dense for the given set of parameters, then one can force the level of refinement to be increased with this keyword.

Note

Large levels of refinement may require significant computational time. Use with caution.

geometry s: Name of geometry set to be used as the surface descriptor of the clump. The surface description must be a closed, orientable, and manifold surface composed of {line segements in 2D; triangular facets in 3D}.

inertia fe11 fe22 fe33 fe12 fe13 fe23 (only 1 component in 2D): Set the inertia “tensor” of the clump in its current configuration. This value of the inertia tensor, {a float in 2D corresponding to the polar moment of inertia; a 2nd order tensor in 3D}. In 3D, 6 parameters must be specified in the order e11,e22,e33,e12,e13,e23 using the row/column convention. One must also specify the volume and this keyword cannot be specified with the pebcalculate or surfcalculate keywords.

name s: Given name of the clump template. If no name is specified and no geometry set is specified, then the name clumpTemplateXX is assigned, where XX is the clump template ID. If no name is specified and a geometry set is specified, then s is the geometry set name.

pebbles inumber frad vpos: Number of pebbles in the clump, inumber, followed by inumber sets of pebble geometric parameters. Each set is the pebble radius (frad) and position (fposx, fposy and fpoz). Cannot be given with the bubblepack keyword.

pebcalculate ftol: This keyword specifies that the clump position, volume, and inertia tensor will be calculated from the pebble distribution assuming constant density. The space containing the clump is recursively subdivided into boxes that are {squares in 2D; cubes in 3D}. The {areas in 2D; volumes in 3D} and inertia tensors of all boxes that fall completely within any pebbles are accumulated. The parallel axis theorem is used to accumulate the inertia tensors. For each iteration, the “final” size of the clump is extrapolated and the iterations cease when either 1) the total number of cells to be subdivided reaches 1e6 or 2) the extrapolated and estimated sizes are within the desired tolerance. By default, the percentage difference ftol = 0.01. The minimum value allowed is 0.00005 and the user should be aware that setting the percentage to such a small value may require some computational effort to calculate these attributes. The clump centroid calculated is assigned to the clump. This command cannot be given with the inertia, position, surfcalculate, volume, x, y, or z keywords.

position vcpos: Clump position that is the origin by default. This is the position of the clump centroid. This keyword cannot be given with the pebcalculate or surfcalculate keywords.

position-x fposx: The x-component of the position that is 0 by default. This keyword cannot be given with the pebcalculate or surfcalculate keywords.

position-y fposy: The y-component of the position that is 0 by default. This keyword cannot be given with the pebcalculate or surfcalculate keywords.

position-z fposz (3D ONLY): The z-component of the position that is 0 by default. This keyword cannot be given with the pebcalculate or surfcalculate keywords.

surfcalculate: Calculate the inertial attributes from the surface description assuming uniform density. The algorithm involves looping through all facets, computing the covariance of the {triangle in 2D; tetrahedron in 3D} formed by the facet vertices and the origin, adding this covariance to an accumulator, and converting the covariance matrix to an inertia tensor. In 2D, the polar moment of inertia is used, which is the trace of the inertia tensor. See http://number-none.com/blow/inertia/index.html for a thorough description of the algorithm. This keyword cannot be given with the inertia, pebcalculate, position, volume, x, y, or z keywords.

volume fvol: Set the {volume per unit thickness in 2D; volume in 3D} to fvol. One must also specify the inertia tensor as well. This keyword cannot be given with the pebcalculate or surfcalculate keywords.

delete s

Delete clump template s with the specified names. If a name is not specified, then all clump templates are deleted. Any clumps referring to the deleted clump template(s) no longer refer to any clump template.

name s: Name of clump template to delete.

export s <keyword ...>

Export the clump template s to file. The default file name is {“clump.p2clp” in 2D; “clump.p3clp” in 3D}. If nothrow is specified, then a file will be overwritten if it exists, otherwise an error is thrown. This is a binary file that can be reloaded with the import keyword.

filename s: Clump template file name that is, by default, the name of the clump template appended with the extentsion {.p2clp in 2D; .p3clp in 3D}.

skip-errors: Indicate that if a previous file of the specified s exists, then it will be overwritten.

import s keyword ...

Import clump template from file with name s. If name is not specified, then the clump name is set to the file name without the file extension. If a clump template with of the specified name exists, then an error is thrown.

name s: Clump template name. If not specified, then the clump name is set to the file name s without the file extension.

Usage Example

The clump template command can be used to create a clump template for later use.

Simple example

In this example, two clump templates will be generated. They will differ in the number of pebbles employed, but they’ll have the same inertial attributes. To do this, (see the clump create usage example for another example), a first clump template composed of three pebbles is generated and its inertial attributes computed using the calculate keyword.

model new
model domain extent -3.0 3.0

clump template create ...
    pebcalculate ...
    name 'three_peb' ...
    pebbles 3 ...
        0.25 -0.55 0.0 0.6 ...
        0.25 -0.75 0.0 0.15 ...
        0.25 -0.75 0.0 0.4

A second clump template is then created, composed of two pebbles, that inherits the inertial attributes of the former.

fish define extract_values(c)
  global volume = clump.template.vol(c)
  global xx_in = clump.template.moi.xx(c)
  global yy_in = clump.template.moi.yy(c)
  global zz_in = clump.template.moi.zz(c)
  global xy_in = clump.template.moi.xy(c)
  global xz_in = clump.template.moi.xz(c)
  global yz_in = clump.template.moi.yz(c)
  global xpos = clump.template.origpos.x(c)
  global ypos = clump.template.origpos.y(c)
  global zpos = clump.template.origpos.z(c)
end
[cl=clump.template.find('three_peb')]
@extract_values(@cl)

clump template create ...
    name 'two_peb' ...
    volume  [volume] ...
    inertia [xx_in] [yy_in] [zz_in] [xy_in] [xz_in] [yz_in] ...
    position [-xpos] [ypos] [zpos] ...
    pebbles 2 ...
        0.25 0.55 0.0 0.6 ...
        0.25 0.75 0.0 0.4

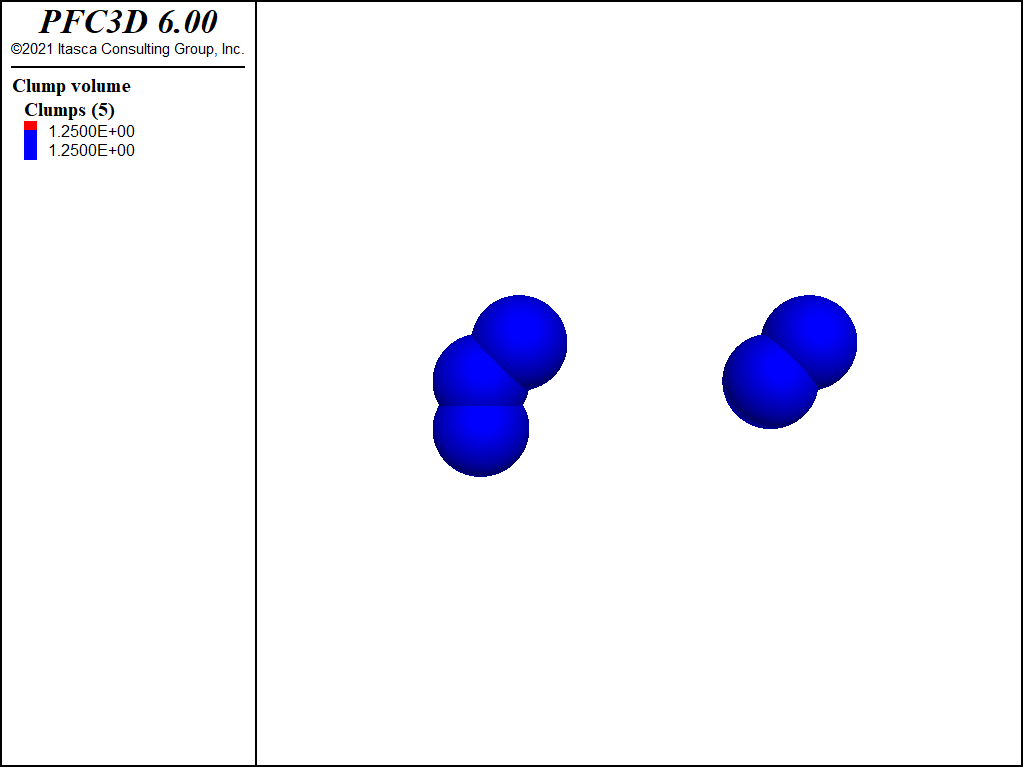
../../../../../../_images/clumptemplate.png

Figure 1: Clump templates created by the clump template command. The two clumps have been defined to have the same inertial attributes (the inertia volume is plotted), even if their geometries differ.

A cloud of clumps is finally generated using the clump distribute command.

clump distribute porosity 0.70           ...
                  resolution 1.0           ...
                  number-bins    2              ...
                  diameter                 ...
                  box -2.5 2.5 ...
                  bin 1 size 0.2 0.2 ...
                        volume-fraction  0.5    ...
                        group 'three_peb' ...
                        template 'three_peb' ...
                            az -90 90       ...
                            el -90 90      ...
                            tilt 0 0       ...  
                  bin 2 size 0.2 0.2 ...
                        volume-fraction  0.5    ...
                        group 'two_peb' ...
                        template 'two_peb' ...
                            az -90 90       ...
                            el -90 90      ...
                            tilt 0 0

../../../../../../_images/clumptemplate2.png

Figure 2: Cloud of clumps comprising two groups of clumps produced by using the clump templates that were created.

Import geometry from external file

Another interesting application of the clump template command is associated with the geometry import command, whereby the surface descriptor of the clump can be imported. Here a .stl file is imported to create a “pill”-shaped clump template.

model new
model domain extent -3.0 3.0

geometry import 'ellipsoid.stl'

clump template create name 'pill' ... 
    geometry 'ellipsoid' ...
    surfcalc bubblepack ratio 0.5 distance 150

../../../../../../_images/clumptemplate3.png

Figure 3: Clump template created using the geometry keyword.

The clump distribute command is finally used again to generate a cloud by using the newly created template. A set of vertically oriented pills are created using the azimuth, elevation, and tilt keywords.

clump distribute porosity 0.70             ...
                  resolution 1.0            ...
                  number-bins    1               ...
                  diameter                  ...
                  group 'pills'               ...
                  box -2.5 2.5 ...
                  bin 1 size 0.2 0.2 ...
                        volume-fraction  1.0     ...
                        template 'pill'       ...
                            az 0 0       ...
                            el 0 0       ...
                            tilt 0 0

../../../../../../_images/clumptemplate4.png

Figure 4: Cloud of “pill”-shaped clumps.

Clumps can be resized using the clump scale command. Also, their orientation can be also modified using the clump rotate command.

clump scale diameter 0.4

clump rotate axis (0,1,0) angle 45

../../../../../../_images/clumptemplate5.png

Figure 5: Resized and rotated clumps.