Clumps in a Box
Introduction
Note
The project file for this example may be viewed/run in PFC.[1] The data files used are shown at the end of this example.
This simple example is similar to the balls in a box tutorial, in that objects are placed in a box and allowed to settle. In this case, though, three clump templates are created to demonstrate the clump template logic (see the clump template command). This example also demonstrates usage of the clump generate, clump attribute, and contact cmat default commands, and makes use of the linear contact model.
Numerical Model
The complete data file (3D) for this example is “clumps_in_a_box.dat (3D)”. Select lines of this file are discussed below, where substantially different from the “Balls in a Box” tutorial. Please review that tutorial for a more thorough description of the domain and Contact Model Assignment Table (CMAT).
As in the ball tutorial, the contact cmat default command is used to select the default mechanical contact model. The linear contact model is also selected but, unlike the previous tutorial, additional contact model properties are specified. In this case, the shear stiffness, normal viscous damping ratio, and friction are specified. These additional contact model properties allow for energy dissipation without the use of local damping.
contact cmat default model linear property kn 1.0e6 ...
ks 5.0e5 dp_nratio 0.5 fric 0.3
The clump template logic is used to create clump objects that can be output as files for subsequent usage (see the clump template export and clump template import commands). A clump template is not a model object in itself; it serves as a basis for creating clumps in the model with the same shape as the clump template. The facilities to create clumps from clump templates include the ability to rotate, translate, and scale the clumps relative to their template. One can simply replicate a clump from a template (see the clump replicate command) or create distributions of clumps (via the clump generate and clump distribute commands, as discussed below).
The first clump template created (see the clump template create command) in this tutorial consists of a single pebble. The full inertia tensor and volume of the clump template are specified explicitly. The number of pebbles, their radii, and locations are also specified. Note that one could set the inertial attributes arbitrarily.
[rad = 0.5]
[vc = (4.0/3.0)*math.pi*(rad)^3]
[moic = (2.0/5.0) * vc * rad^2]
clump template create name 'single' ...
pebbles 1 ...
[rad] 0 0 0 ...
volume [vc] ...
inertia [moic] [moic] [moic] 0 0 0
The second clump template uses a different approach to calculate the inertial attributes. In this case, the clump consists of two overlapping pebbles with the same radii. One can analytically calculate the volume and inertia tensor of this configuration, or use the pebcalculate keyword to calculate these parameters from the pebble configuration. A voxelization approach is used: it recursively subdivides the volume occupied by the pebbles into {squares in 2D; cubes in 3D} to estimate the inertial attributes to a specified tolerance.
clump template create name 'dyad' ...
pebbles 2 ...
[rad] [-rad*0.5] 0 0 ...
[rad] [rad*0.5] 0 0 ...
calculate-pebbles 0.005
The third clump template uses yet another approach to specify both the pebbles and the inertial attributes. This clump template is based on an .stl surface description of a dolos as shown below. Dolosse are used to protect coastal areas from erosion due to wave action.
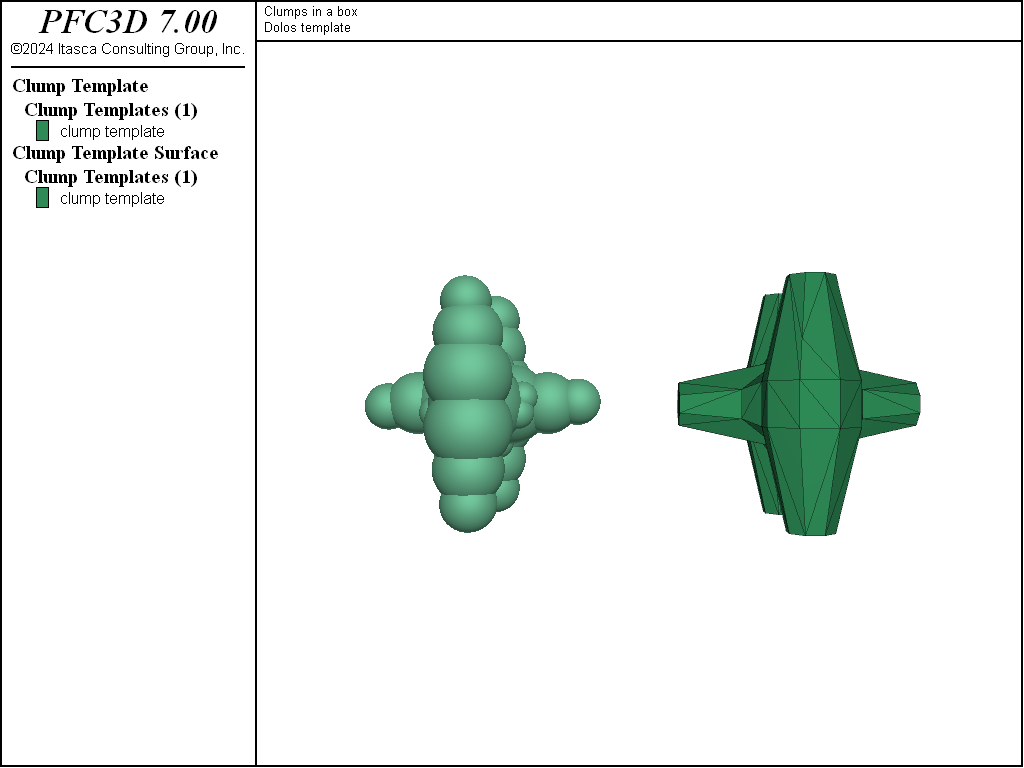
Figure 1: The dolos surface description (right) and resulting pebble distribution (left) from the BubblePack algorithm.
It may be rather difficult to manually specify the inertial attributes and pebble locations of a clump template representing this geometry. Instead, the triangulated, closed, and manifold surface description of the dolos is imported as a geometry set (see the geometry import command), and this geometry set is used to calculate the inertial properties of this shape using the surfcalculate keyword. The pebbles are automatically calculated via an approximation of the medial surface of the dolos using the bubblepack algorithm. Both convex and concave geometries can be automatically filled via this algorithm in both 2D and 3D. The ratio keyword specifies the ratio of the smallest to largest pebble in the clump template, while the distance keyword specifies an angular measure of the smoothness of the pebble distribution. In this way, one can control the fidelity with which the pebble distribution matches the surface representation. The surface is not used to resolve contacts; the pebbles alone are used for this purpose. The surface description is a tool that can be used to define the pebble radii/locations and the inertial attributes. An additional benefit of providing a surface description is that clumps may be visualized by this surface description, as shown below.
geometry import 'dolos.stl'
clump template create name 'dolos' ...
geometry 'dolos' ...
bubblepack ratio 0.3 distance 120 ...
calculate-surface
Subsequent to the generation of the material vessel in which clumps will settle, the clumps are generated with the clump generate command. This command places clumps in a box without overlap. The first set of generated clumps have random orientations and volumes equivalent to a sphere with diameter 1.5. The volume and inertia tensors are scaled automatically. In this case, all clump templates are sampled equally to generate 50 clumps. The group specifier bottom is set for these 50 clumps.
clump generate diameter size 1.5 number 50 ...
box -5.0 5.0 -5.0 5.0 -5.0 0.0 ...
group 'bottom'
One may wish to control both the proportion of clumps based on specified templates and their orientations relative to the template orientations. The code below accomplishes both of these goals via the templates, azimuth, elevation, and tilt keywords. Notice that multiple clump generate commands can be given with the same spatial box, and that the clumps generated from these separate operations do not overlap.
As with balls, an additional command exists (clump distribute) to create a set of clumps meeting a target porosity where overlaps are allowed. This logic works similarly for balls and clumps. See the “Replicating a Particle Size Distribution” tutorial for a simple example.
clump generate diameter size 1.5 number 25 ...
box -5.0 5.0 -5.0 5.0 0.0 5.0 ...
templates 2 ...
'dyad' 0.3 'dolos' 0.7 ...
azimuth 45.0 45.0 ...
tilt 90.0 90.0 ...
elevation 45.0 45.0 ...
group 'top1'
clump generate diameter size 1.5 number 25 ...
box -5.0 5.0 -5.0 5.0 0.0 5.0 ...
templates 2 ...
'dyad' 0.7 'dolos' 0.3 ...
azimuth -45.0 -45.0 ...
tilt 90.0 90.0 ...
elevation 45.0 45.0 ...
group 'top2'

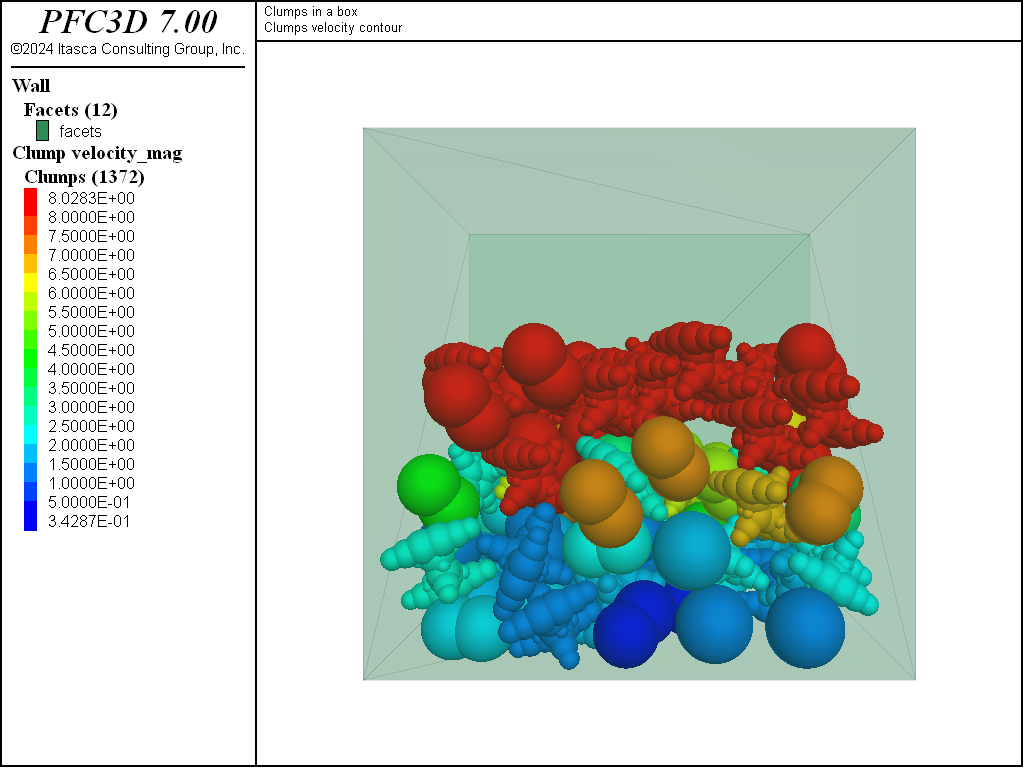
Figure 2: Clumps colored by their group identifiers. The groups correspond to different instances of
the clump generate command and do not overlap.
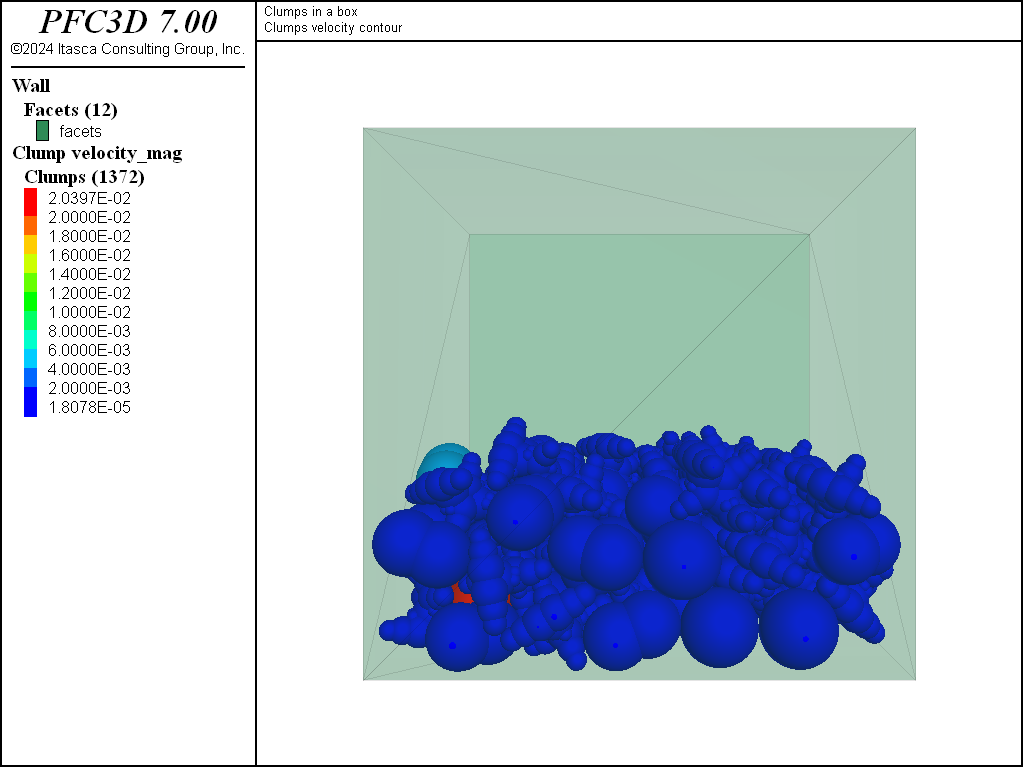
The clumps are then allowed to settle in the box under gravity. At an intermediate stage of settling, one can see that many of the clumps near the top of the model are moving uniformly under gravity. These clumps did not overlap at generation and continue to fall adjacent to one another with the same velocity. The clumps quickly reach equilibrium in the box.
Discussion
This example introduces the clump template logic and the main steps to build a simple PFC model out of clumps. Philosophical questions arise from this capability: What does a clump represent? Should a clump have the inertial attributes of a surface defining its geometry? Should the clump inertial attributes correspond to the actual pebble attributes used for contact resolution? This logic allow for both approaches.
Data Files
clumps_in_a_box.dat (3D)
; fname: clumps_in_a_box.dat
;
; Exercise clump template creation and generation
;=========================================================================
model new
model large-strain on
model title 'Clumps in a box'
; Set the domain extent and the random seed
model domain extent -10.0 10.0
model random 12001
; Modify the default slots of the Contact Model Assignment Table
; Here we choose the linear contact model for all contact types
; excerpt-ixsz-start
contact cmat default model linear property kn 1.0e6 ...
ks 5.0e5 dp_nratio 0.5 fric 0.3
; excerpt-ixsz-end
; Create a clump template, specifying the inertia tensor and volume
; excerpt-myzu-start
[rad = 0.5]
[vc = (4.0/3.0)*math.pi*(rad)^3]
[moic = (2.0/5.0) * vc * rad^2]
clump template create name 'single' ...
pebbles 1 ...
[rad] 0 0 0 ...
volume [vc] ...
inertia [moic] [moic] [moic] 0 0 0
; excerpt-myzu-end
; Create a clump template, specifying the calculation of the
; inertial properties from the pebbles via voxelization
; excerpt-jnxu-start
clump template create name 'dyad' ...
pebbles 2 ...
[rad] [-rad*0.5] 0 0 ...
[rad] [rad*0.5] 0 0 ...
calculate-pebbles 0.005
; excerpt-jnxu-end
; Create a clump template from an stl file, filling it with
; the bubblepack algorithm
; excerpt-ltms-start
geometry import 'dolos.stl'
clump template create name 'dolos' ...
geometry 'dolos' ...
bubblepack ratio 0.3 distance 120 ...
calculate-surface
; excerpt-ltms-end
; Generate a containing box
wall generate box -5.0 5.0 one-wall
; Generate clumps in one box without orientation control, drawing
; equally from all clump templates
; excerpt-pnqn-start
clump generate diameter size 1.5 number 50 ...
box -5.0 5.0 -5.0 5.0 -5.0 0.0 ...
group 'bottom'
; excerpt-pnqn-end
; Generate clumps in another box with orientation control, drawing
; unequally from the templates
; excerpt-yhhr-start
clump generate diameter size 1.5 number 25 ...
box -5.0 5.0 -5.0 5.0 0.0 5.0 ...
templates 2 ...
'dyad' 0.3 'dolos' 0.7 ...
azimuth 45.0 45.0 ...
tilt 90.0 90.0 ...
elevation 45.0 45.0 ...
group 'top1'
clump generate diameter size 1.5 number 25 ...
box -5.0 5.0 -5.0 5.0 0.0 5.0 ...
templates 2 ...
'dyad' 0.7 'dolos' 0.3 ...
azimuth -45.0 -45.0 ...
tilt 90.0 90.0 ...
elevation 45.0 45.0 ...
group 'top2'
; excerpt-yhhr-end
; Assign clump density
clump attribute density 100.0
; Activate gravity
model gravity 10.0
;Save the initial state
model save 'initial-state'
; Solve for a given time and save the model
model solve time 0.8
model save 'intermediate-time'
; Solve again to equilibrium and save the model
model solve ratio-average 1e-4
model save 'final-model'
program return
;=========================================================================
; eof: clumps_in_a_box.dat
Endnotes
| [1] | To view this project in PFC, use the program menu.
⮡ PFC |
| Was this helpful? ... | PFC © 2021, Itasca | Updated: Feb 25, 2024 |