Tips and Advice
When problem solving with FLAC3D, it is important to optimize the model for the most efficient analysis. This section provides several suggestions on ways to improve a model run, as well as some common pitfalls to be avoided when preparing a FLAC3D calculation.
1. Check Model Runtime
The solution time for a FLAC3D run is proportional to \(N^{4/3}\), where \(N\) is the number of zones. This formula holds for elastic problems solved for the equilibrium condition. The runtime will vary somewhat, but not substantially, for plasticity problems, and it may be much larger if continuing plastic flow occurs. It is important to check the speed of calculation on your computer for a specific model. An easy way to do this is to run the benchmark test below. Then use this speed to estimate the speed of calculation for the specific model based on interpolation from the number of zones.
2. Effects on Runtime
FLAC3D will take longer to converge if:
- there are large contrasts in stiffness in zone materials or between zones, structural members and interfaces; or
- there are large contrasts in zone sizes.
The code becomes less efficient as these contrasts become greater. The effect of a contrast in
stiffness should be investigated before performing a detailed analysis. For example, a very
stiff loading plate can be replaced by a series of fixed gridpoints that are given a constant
velocity. (Remember that the zone face apply or zone gridpoint fix commands may be
used to fix velocities, not displacements.) The inclusion of groundwater will act to increase
the apparent mechanical bulk modulus (see the Fluid-Mechanical Interaction section).
It is possible that the overall model response of interest may not be significantly affected by requiring full convergence of small stiff regions (due to material properties or zone size). In this case, using the convergence solve criteria and increasing the ratio-target of the area may significantly decrease the required run time. As always, carefully analyze the model response to be satisfied that this is an acceptable additional error.
3. Considerations for Zoning Density
FLAC3D uses constant-strain elements. If the stress/strain gradient is high, you will need many zones to represent the varying distribution. Run the same problem with different zoning densities to check the effect.
Try to keep the zoning as uniform as possible, particularly in the region of interest. Avoid
long, thin zones with aspect ratios greater than 5:1, and avoid jumps in zone size (i.e., use
smoothly graded grids). Make use of the ratio keyword with the zone create
command to grade zone sizes smoothly from regions with fine zoning to regions with coarse
zoning. If zone densification has been done with zone densify, we recommend using the
gradient-limit keyword to minimize the zone size gradient.
4. Automatic Detection of an Equilibrium State
As discussed in Reaching Equilibrium, we recommend you use the convergence 1.0
limit criteria when using the model solve command. However, you should always take
displacement and velocity histories of the areas of most interest, and determine if sufficient
equilibrium will be reached sooner, or if further cycling is still necessary. Initially
solving to a convergence of 100 or more and then examining the response is good
practice. Making isosurface plots of convergence to see where the model is having trouble can
give insight into where model adjustments in the interest of efficiency are best placed.
The default ratio limit is also used to detect the steady-state solution for thermal and fluid-flow calculations. For thermal calculations, unbalanced and applied heat flux magnitudes, rather than unbalanced and applied mechanical forces, are evaluated. For fluid-flow calculations, the unbalanced and applied fluid flow magnitudes are evaluated.
5. Considerations for Selecting Damping
The default mechanical damping for static analysis is local damping (see the topic Mechanical Damping), which is most efficient for removing kinetic energy when the velocity components of most gridpoints pass through zero periodically. This is because the mass-adjustment process depends on velocity sign changes. Local damping is a very efficient algorithm for achieving a static-equilibrium solution without introducing erroneous damping forces (see Cundall 1987).
If the problem involves significant regions of the grid having nonzero components of velocity at
the final state of solution, then the default damping may be insufficient to reach an
equilibrium state. A different form of damping, known as combined damping, provides better
convergence to the steady-state than local damping for situations in which significant
rigid-body motion of the grid is occurring. This may occur, for example, in a creep simulation
or in a very stiff structural reinforcement attached to soft soil moving in response to an
excavation. Use the command zone mechanical damping combined to invoke combined damping.
Combined damping is not as efficient at removing kinetic energy, so be careful to minimize
dynamic excitation of the system (see the gradual excavation of a circular tunnel example). It is possible to switch back to the default damping with the command zone mechanical damping local.
6. Check Model Response
FLAC3D shows how a similar physical system would behave. Make frequent simple tests to verify that you are actually doing what you think you are doing. For example, if a loading condition and geometry are symmetrical, make sure that the response is symmetrical. After making a change in the model, execute a few calculation steps (say, 50 or 100) to verify that the initial response is of the correct sign and in the correct location. Do back-of-the-envelope estimates of the expected order of magnitude of stress or displacements, and compare to the FLAC3D output.
If you apply a violent shock to the model, you will get a violent response. If you do nonphysically reasonable things to the model, you must expect strange results. If you get unexpected results at a given stage of an analysis, review the steps you followed up to that stage.
Critically examine the output before proceeding with the model simulation. If, for example, everything appears reasonable except for large velocities in one corner zone, do not go on until you understand the reason. In this case, you may not have fixed a boundary gridpoint properly.
7. Initializing Variables
It is common practice to initialize the displacements of the gridpoints between runs to aid in the interpretation of a simulation in which many different excavation stages are performed. This can be done because the code does not require the displacements in the calculation sequence — they are determined from the velocities of the gridpoints as a convenience to the user.
Initialization of the velocities, however, is a different matter. If the velocities of gridpoints are fixed at a constant value, they will continue to have this value until set otherwise. Therefore, do not initialize the velocities of the grid to zero simply to clear them—this will affect the simulation results. However, sometimes it is useful to set velocities to zero (for example, to remove all kinetic energy).
8. Minimizing Transient Effects on Static Analysis
For static analyses, transient waves can cause plastic models to follow poorly defined stress paths (unrealistic failure could be triggered). For this reason, it is often important to approach the solution (at each stage) gradually (i.e., make the solution more “static” by minimizing the effects of transient waves when problem conditions are changed suddenly.[1]
The recommended method to make a FLAC3D solution more static is to use
zone relax excavate to excavate regions, and the servo option on
zone face apply when applying or reducing loads. When a sudden change is made (e.g., by
nulling zones to simulate excavation), it is not advisable to set the strength properties to
high values and step to equilibrium (and then reset the properties to realistic values). This
latter method does not clearly define a direction in stress space to bring a zone within the
yield surface (the entire process is nonphysical).
9. Changing Material Models
FLAC3D does not have a limit on the number of different material models you may use during a simulation. The code has been dimensioned to allow the user to have a different material for each zone (if desired) for the maximum size grid for your version of FLAC3D.
10. Running Problems with In-Situ Field Stresses and Gravity
There are a number of problems in which in-situ field stresses and gravity must be applied to the model. An example of such a problem is deep cut-and-fill mining, in which the rock mass is subjected to high in-situ stress fields (i.e., gravity stresses for the limited mesh size can be ignored), but in which the emplaced backfill pillars develop gravitational stresses that could collapse under the load. The important thing to note in these simulations (as in any simulation in which gravity is applied) is that at least three points on the grid must be fixed in space; otherwise, the entire grid will translate due to gravity. If you ever notice the entire grid translating in the direction of the gravitational acceleration vector, you have probably forgotten to fix the grid in space (e.g., see uplift when material is removed).
11. Determining Collapse Loads
In order to determine a collapse load, it is often better to use “strain-controlled” rather than “stress-controlled” boundary conditions (i.e., apply a constant velocity and measure the reaction forces, rather than apply forces and measure displacements). A system that collapses becomes difficult to control as the applied load approaches the collapse load. This is true of a real system as well as a model system.
12. Determining Factor of Safety
Factor of safety can be determined in FLAC3D for any selected parameter by taking the ratio of the calculated value under given conditions to the value that results in failure. For example:
Note that the larger value is always divided by the smaller value (assuming that the system does not fail under the actual conditions). The definition of failure must be established by the user. A comparison of this approach, which is based on strength reduction for determining factor of safety, to that based upon limit analysis solutions is given by Dawson and Roth (1999) and Dawson et al. (1999). Also see the example application Influence of Slope Curvature on Stability.
The strength reduction method for determining factor of safety is implemented in FLAC3D
through the model factor-of-safety command. This command implements an automatic search
for factor of safety using the bracketing approach, as described in Dawson et al. (1999). The
model factor-of-safety command may be given at any stage in a FLAC3D run, provided that
every non-null zone contains a constitutive model that supports property scaling. During the
solution process, properties will be changed, but the original state will be restored on
completion, or if the factor-of-safety search is terminated prematurely with the
Esc key.
When FLAC3D is executing the model factor-of-safety command, the bracketing values for
\(F\) are printed continuously to the screen so that you can tell how the solution is
progressing. If terminated by the Esc key, the solution process terminates, and the best
current estimate of fos is displayed. A save file that corresponds to the last
nonequilibrium state is produced so that velocity vectors, and so on, can be plotted. This
allows a visualization of the failure mode.
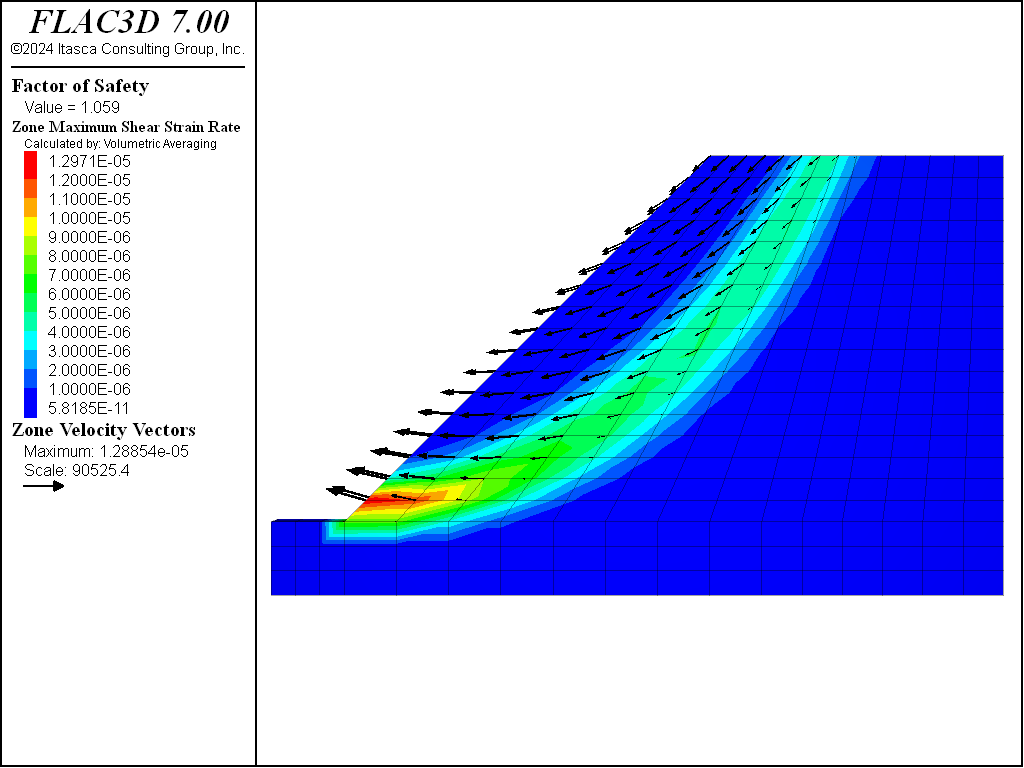
The example below, based upon an example stability analysis from Dawson et al. (1999), illustrates how the approach works. The corresponding project file is “FactorOfSafety.prj.” The run stops at \(F\) = 1.06. The figure that follows plots shear strain-rate contours and velocity vectors, which allow the failure surface to be identified.
Factor of safety calculation for slope stability analysis
model new
model large-strain off
; Create zones
zone create brick point 0 (0, 0,0) point 1 (2,0,0) ...
point 2 (0,0.5,0) point 3 (0,0,2) ...
size 3 1 3
zone create brick point 0 (2, 0,0) point 1 (13.4,0,0) ...
point 2 (2,0.5,0) point 3 ( 2,0,2) ...
size 8 1 3
zone create brick point 0 (13.4, 0,0) point 1 (20 ,0,0) ...
point 2 (13.4,0.5,0) point 3 (13.4,0,2) ...
size 6 1 3
zone create brick point 0 ( 2 , 0, 2) point 1 (13.4, 0, 2) ...
point 2 ( 2 ,0.5, 2) point 3 (12 , 0,12) ...
point 4 (13.4 0.5, 2) point 5 (12 ,0.5,12) ...
point 6 (16 , 0,12) point 7 (16 ,0.5,12) ...
size 8 1 17
zone create brick point 0 (13.4, 0, 2) point 1 (20, 0,2 ) ...
point 2 (13.4,0.5, 2) point 3 (16, 0,12) ...
point 4 (20 ,0.5, 2) point 5 (16,0.5,12) ...
point 6 (20 , 0,12) point 7 (20,0.5,12) ...
size 6 1 17
zone face skin
; Constitutive model and properties
zone cmodel assign mohr-coulomb
zone property density 2000.0 bulk 1e8 shear 3e7 cohesion 12380 tension 1e10 ...
friction 20 dilation 20
; Boundary conditions
zone face apply velocity-normal 0 range group 'East' or 'West'
zone face apply velocity-normal 0 range group 'North' or 'South'
zone face apply velocity (0,0,0) range group 'Bottom'
; Initial conditions
model gravity 10
zone initialize-stresses
; Histories
model history name='conv' mechanical convergence
; Solve
model solve convergence 1
model factor-of-safety file 'slope3dfos' associated convergence 1
It is recommended that the model factor-of-safety command be given at an equilibrium
state of a model (to improve solution time and reduce possible pseudo-inertial effects), but
this is not essential.
The procedure used by FLAC3D during execution of model factor-of-safety is as follows.
First, the code finds a “representative number of steps” (denoted by \(N_r\)),
which characterizes the response time of the system. \(N_r\) is found by setting
the cohesion to a large value, making a large change to the internal stresses, and finding how
many steps are necessary for the system to return to equilibrium. Then, for a given factor of
safety, \(F\), \(N_r\) steps are executed. If the equilibrium condition is
met, then the system is in equilibrium. If the condition is not met, then another \(N_r\) steps are executed, exiting the loop if the condition is met. The equilibrium
condition value, averaged over the current span of \(N_r\) steps, is compared with the mean
force ratio over the previous \(N_r\) steps. If the difference is less than 10%, the system
is deemed to be in nonequilibrium, and the loop is exited with the new nonequilibrium, \(F\).
If the above-mentioned difference is greater than 10%, blocks of \(N_r\) steps are
continued until: 1) the difference is less than 10%; 2) 6 such blocks have been executed; or
3) the equilibrium condition is met. The justification for the first case is that the mean force
ratio is converging to a steady value that is greater than that corresponding to equilibrium;
the system must be in continuous motion. The FISH intrinsic variable global.fos allows
access to the current value of \(F\) during model factor-of-safety execution (see
example this needs to go to example 2.18 in FISH book “example use of fos_f”).
13. Use Bulk and Shear Moduli
It is better to use bulk modulus, \(K\), and shear modulus, \(G\), than Young’s modulus, \(E\), and Poisson’s ratio, \(ν\), for elastic properties in FLAC3D.
The pair (\(K,G\)) makes sense for all elastic materials that do not violate thermodynamic principles. The pair (\(E,ν\)) does not make sense for certain admissible materials. At one extreme, we have materials that resist volumetric change but not shear; at the other extreme, materials that resist shear but not volumetric change. The first type of material corresponds to finite \(K\) and zero \(G\), and the second to zero \(K\) and finite \(G\). However, the pair (\(E,ν\)) is not able to characterize either the first or the second type of material. If we exclude the two limiting cases (conventionally, \(ν\) = 0.5 and \(ν\) = -1), the equations
relate the two sets of constants. These equations hold, however close we approach (but not reach) the limiting cases. We do not need to relate them to physical tests that may or may not be feasible; the equations are simply the consequence of two possible ways of defining coefficients of proportionality. Suppose we have a material in which the resistance to distortion progressively reduces, but the resistance to volume change remains constant. \(ν\) approaches 0.5 in this case. The equation \(3K(1 - 2ν) = E\) must still be satisfied. There are two possibilities (argued on algebraic, not physical, grounds): either \(E\) remains finite (and nonzero) and \(K\) tends to an arbitrarily large value; or \(K\) remains finite and \(E\) tends to zero. We rule out the first possibility because there is a limiting compressibility to all known materials (e.g., 2 GPa for water, which has a Poisson’s ratio of 0.5). This leaves the second, in which \(E\) is varying drastically, even though we supposed that the material’s principal mode of elastic resistance was unchanging. We deduce that the parameters (\(E,ν\)) are inadequate to express the material behavior.
FLAC3D Runtime Benchmark
FLAC3D has been tested on a number of different computers. The calculation rates are compared here for a 624,000-zone model footing in a Mohr-Coulomb material. The model is run for 100 steps, and the rate is calculated by a FISH function. The data file is given in the example below; the table that follows summarizes the calculation rates for different computers.
Benchmark Data File — “timing-test.dat”
model new
model large-strain off
; Create zones
zone create cylindrical-shell point 0 (0, 0, 0) point 1 ( 0,15, 0) ...
point 2 (0, 0,15) point 3 (15, 0, 0) ...
point 4 (0,15,15) point 5 (15, 0,15) ...
point 8 (0, 3, 0) point 9 ( 3, 0, 0) ...
point 10 (0, 3,15) point 11 ( 3, 0,15) ...
size 100 80 60 30 ...
ratio 1.05 1.1 1 0.875 fill group 'cyl'
zone face skin
zone face group 'slab' slot 'app' range group 'Top' group 'cyl'
; Constitutive model and properties
zone cmodel assign mohr-coulomb
zone property bulk 2e8 shear 1e8 cohesion 1e5
zone property friction 20 dilation 20 tension 1e10
; Boundary Conditions
zone face apply velocity-normal 0 range group 'West'
zone face apply velocity-normal 0 range group 'South'
zone face apply velocity-normal 0 range group 'Bottom'
zone face apply velocity-normal 0 range group 'North'
zone face apply velocity-normal -2e-5 range group 'slab'
; Initial conditions
zone initialize stress xx -1e6 yy -1e6 zz -1e6
; Measure rate
fish define startClock
global start = time.clock
end
fish define endClock
global time = (global.cycle * zone.num) / ((time.clock-start) / 100)
end
fish callback add startClock event zone_update_complete
fish callback add endClock event solve_complete
model cycle 100
[io.out('Calculation rate = '+string(time/1000)+' kilo-zones/sec')]
Endnotes
| [1] | This is not always the case. “Path-dependency” of a changing nonlinear system can be important. See the discussion in Localization, Physical Instability, and Path-Dependence. |
| Was this helpful? ... | FLAC3D © 2019, Itasca | Updated: Feb 25, 2024 |