Cylindrical Hole in an Infinite Mohr-Coulomb Material (FLAC2D)
Problem Statement
Note
The project file for this example is available to be viewed/run in FLAC2D.[1] A representative sample of the data file used for the structured quadrilateral grid and associated flow is shown at the end of this example. The remaining data files can be found in the project.
Stresses and displacements are determined numerically for the case of a cylindrical hole in an infinite elasto-plastic material subjected to in-situ stresses. The material is assumed to be linearly elastic, perfectly plastic, with a failure surface defined by the Mohr-Coulomb criterion, and both associated (dilatancy = friction angle) and nonassociated (dilatancy = 0) flow rules are used. The results of the simulation are compared with an analytic solution.
This problem tests the Mohr-Coulomb plasticity model under plane-strain conditions and it is solved numerically in FLAC2D.
The Mohr-Coulomb material is assigned several properties.
shear modulus (\(G\)) |
2.8 GPa |
bulk modulus (\(K\)) |
3.9 GPa |
cohesion (\(c\)) |
3.45 MPa |
friction angle (\(\phi\)) |
30° |
dilation angle (\(\psi\)) |
0° and 30° |
The isotropic in-situ stress has a magnitude of -30 MPa, and the pressure inside the hole may be neglected. (As a convention, compressive stresses are negative.)
Closed-Form Solution
The analytic solution for this problem may be found in Salençon (1969). The yield zone radius, \(R_0\), may be expressed in general terms as
in which \(a\) is the hole radius, \(P_0\) is the absolute value of the in-situ isotropic stress, \(P_i\) is the pressure inside the hole (0 Pa, in this case), and
The radial stress at the elastic/plastic interface may be written as
The stresses in the plastic zone have the form
in which \(r\) is the distance from the hole axis.
The stresses in the elastic zone are
The displacements in the elastic region are given as
and, in the plastic region, as
in which
and
In these equations, \(\nu\) is Poisson’s ratio, \(\psi\) is the dilation angle and \(G\) is the shear modulus.
FLAC2D Model
For modeling purposes, the problem is defined by the domain presented in Figure 1; the quarter-symmetry geometry of the problem is exploited. The boundary conditions applied to this domain are also shown in Figure 1. The domain is discretized into 900 zones organized in a radial pattern (for the case of a structured quadrilateral grid).
In the numerical simulation, the initial stress state (corresponding to \(P_0\) = 30 MPa) is applied throughout the domain.
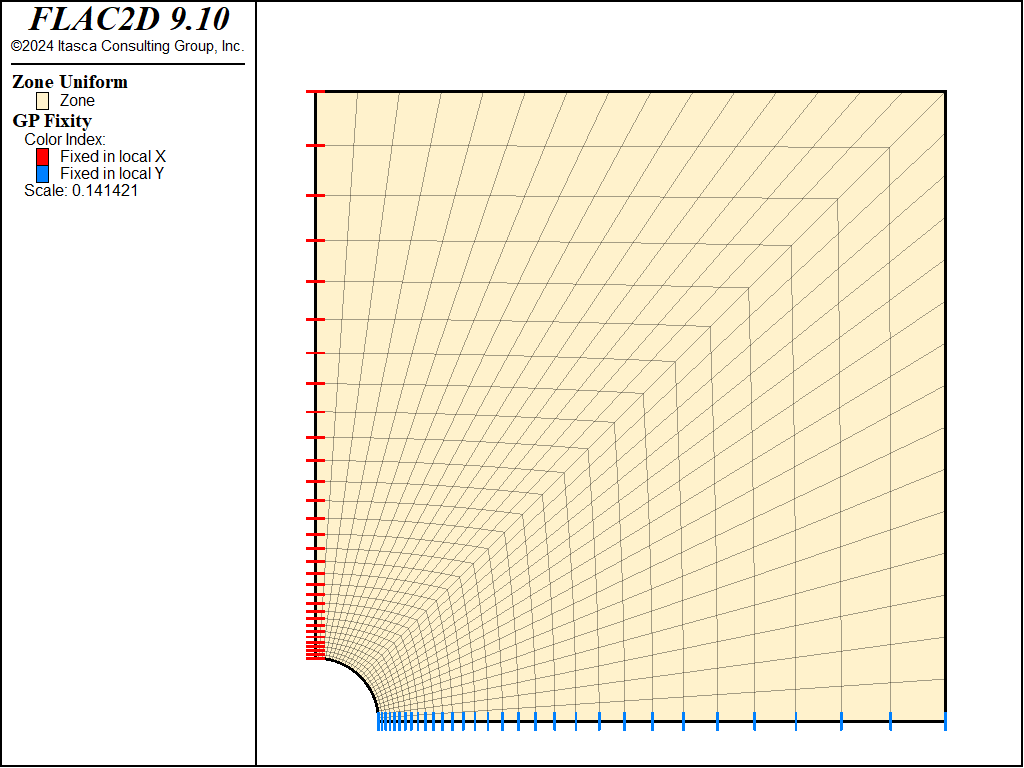
Figure 1: Domain, grid, and boundary conditions for FLAC2D simulation—quarter symmetry.
Results and Discussion
Figure 2 through Figure 5 show comparisons between FLAC2D results and the analytic solution along a radial line. Normalized stresses, \(-{\sigma}_r/P_0\) and \(-{\sigma}_{\theta}/P_0\), are plotted versus normalized radius, \(r/a\), in Figure 2 and Figure 3, while normalized displacements, \(-u_r/a\), are represented versus \(r/a\) in Figure 4 and Figure 5.
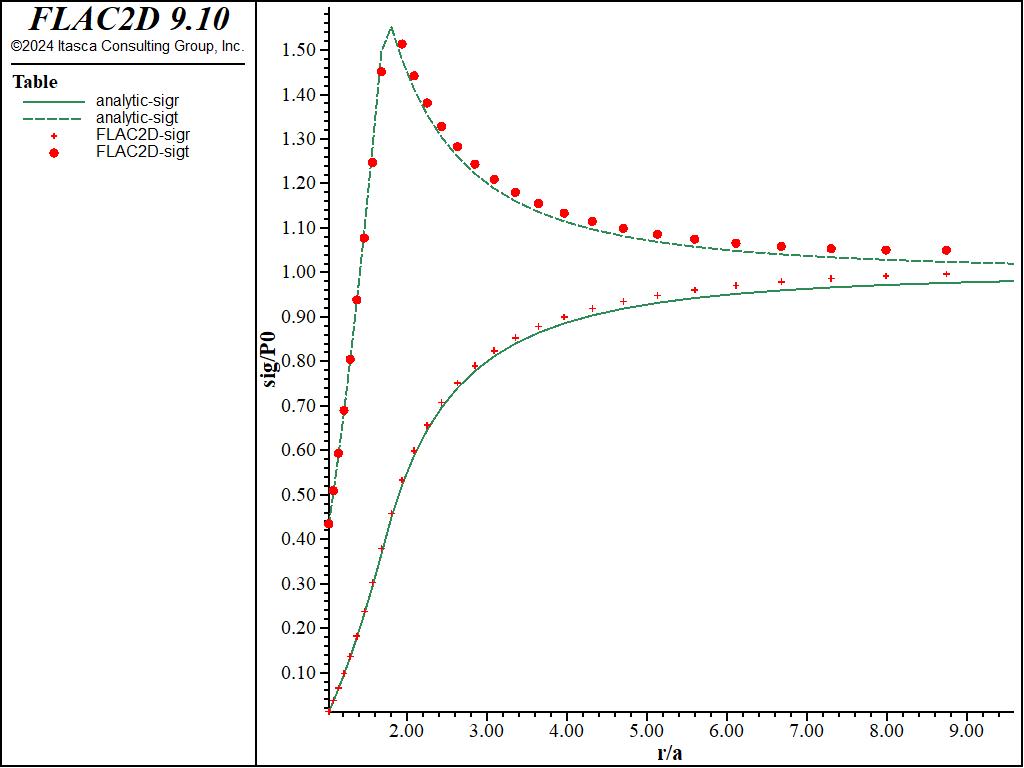
Figure 2: Stress solution comparison—associated (analytical values = lines; numerical values = crosses/circles).
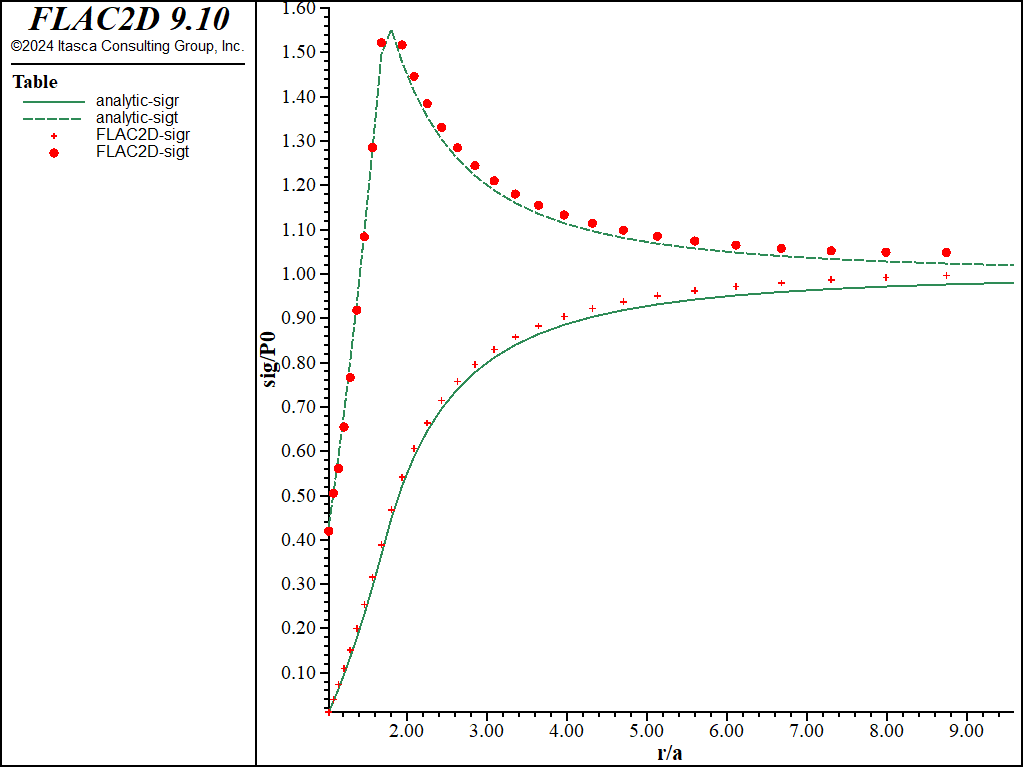
Figure 3: Stress solution comparison—nonassociated (analytical values = lines; numerical values = crosses/circles).
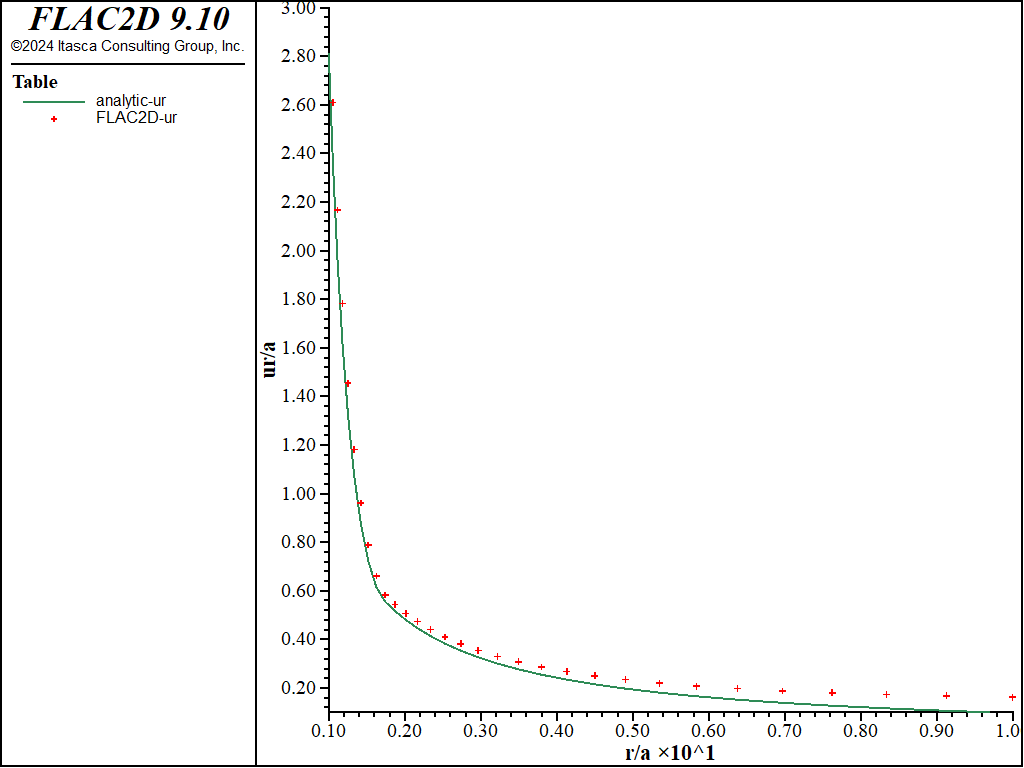
Figure 4: Radial displacement solution comparison—associated (analytical values = lines; numerical values = crosses).
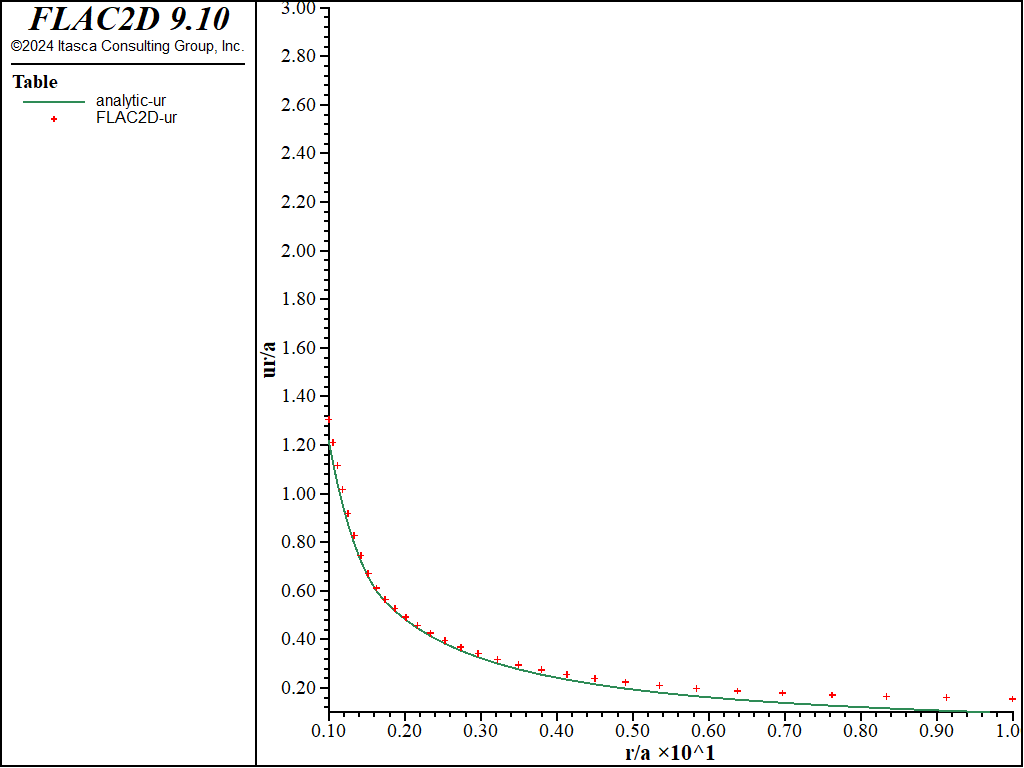
Figure 5: Radial displacement solution comparison—nonassociated (analytical values = lines; numerical values = crosses).
The average relative error on the stresses and displacements is less than 3% throughout the grid. (Note that the error could be reduced by more appropriate handling of the far field conditions using, for example, the Lamé solution for a thick ring.)
Displacement contours and displacement vectors for the associated case are presented in Figure 6, as an illustration.
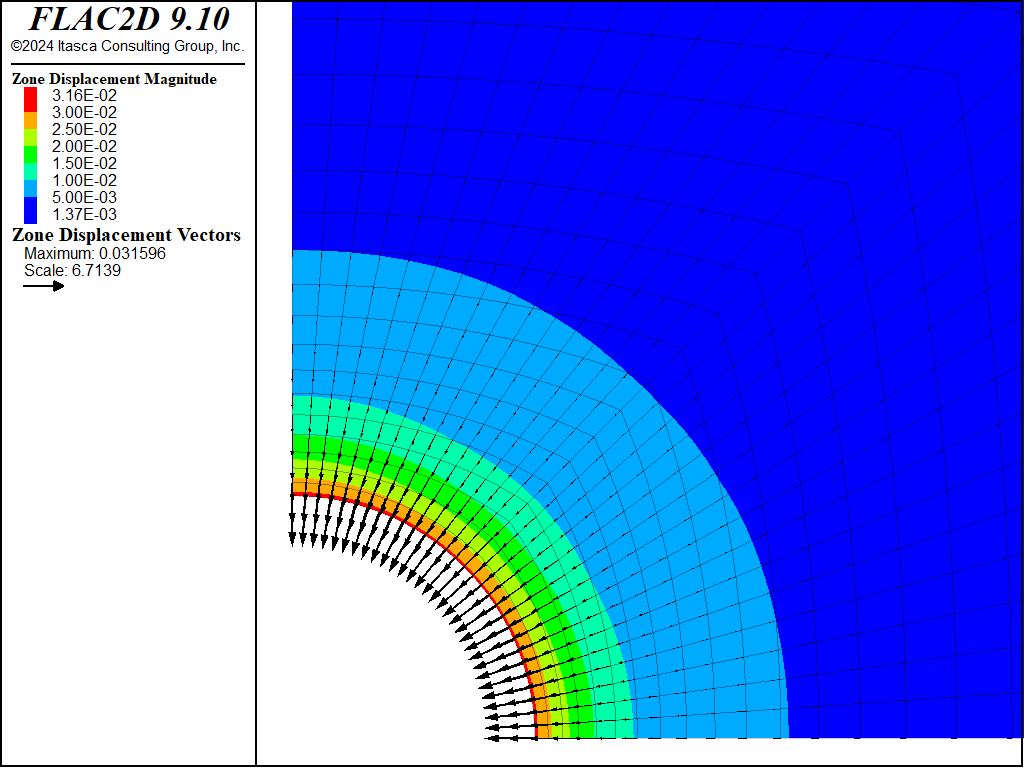
Figure 6: FLAC2D displacement contours and displacement vectors—associated.
The file associated.dat used to generate the associated case is shown below and non-associated.dat is different only in the dilatation value assigned and can be found in the project. (The dilatation angle is 30° in the associated case.)
The files associated-nmd.dat, non-associated-nmd.dat (triangular grid) and associated-nmd-mix.dat, non-associated-nmd-mix.dat (mixed grid) generate the same two cases, but using FLAC2D’s nodal mixed discretization (NMD) feature and unstructured grids with triangular zones only or mixed quadrilateral-triangular zones, respectively (grids are imported from files nmd_tri.f2grid and nmd_mix.f2grid). The NMD calculations are automatically executed for all triangular zones if the NMD option is not explicitly specified (however, it can be turned on or off via the zone nodal-mixed-discretization command). For illustration, only results from the case of the triangular grid are shown below.
The file sale.dat compares the numerical solutions to the analytical solution using FISH functions:
nastrcalculates (i) numerical and corresponding analytical values of \(-{\sigma}_r/P_0\) and \(-{\sigma}_{\theta}/P_0\) at the centroid of zones closest to the \(x\)-axis; and (ii) average relative error of \(-{\sigma}_r/P_0\) and \(-{\sigma}_{\theta}/P_0\) throughout the grid.
nadiscalculates (i) numerical and analytical values of \(u_r/a\) at gridpoints located on the \(x\)-axis; and (ii) the average relative error of the displacement \(u_r/a\) throughout the grid.
The resulting errors are within 3% of the analytical solution for stresses and displacements for both associated and nonassociated flow rules for the triangular grid. Figure 7 through Figure 10 show the NMD results that correspond directly with Figure 2 through Figure 6 (results with an all-quad grid). As can be seen, the results are very similar.
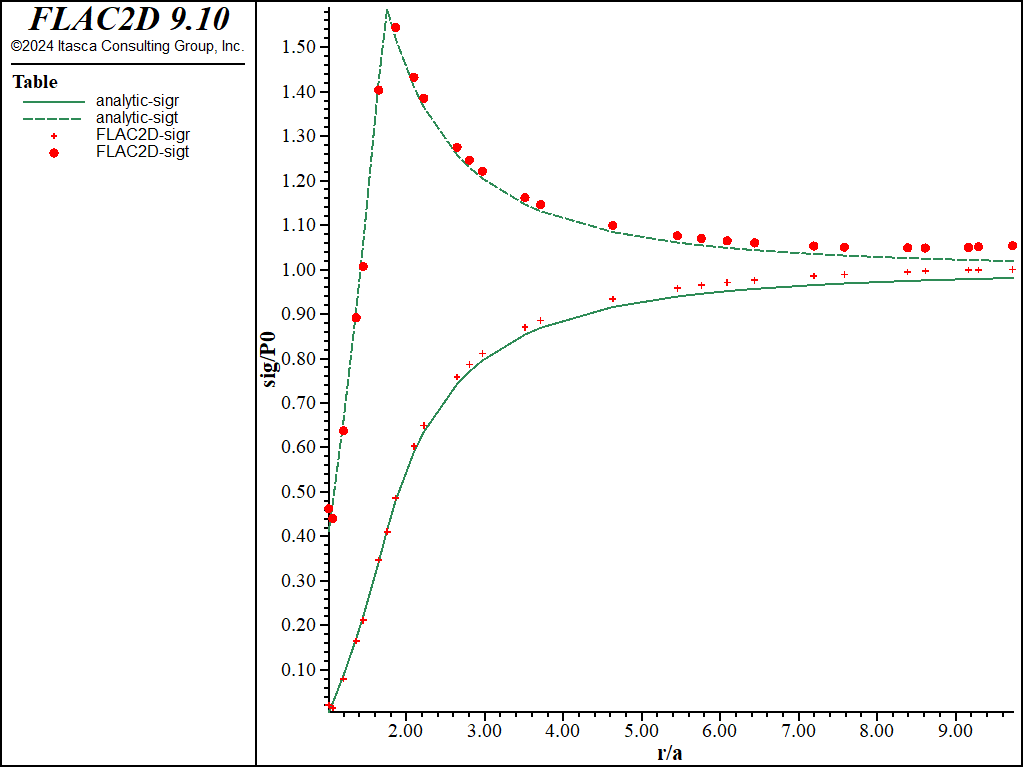
Figure 7: NMD stress solution comparison—associated (analytical values = lines; numerical values = crosses/circles).
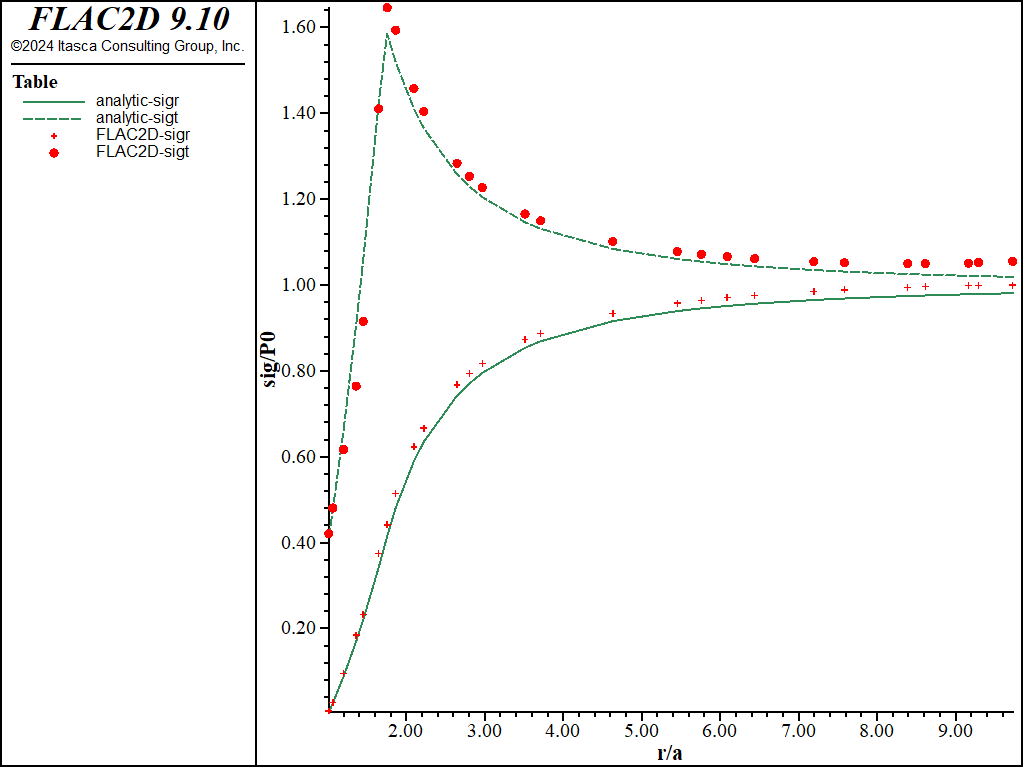
Figure 8: NMD stress solution comparison—nonassociated (analytical values = lines; numerical values = crosses/circles).
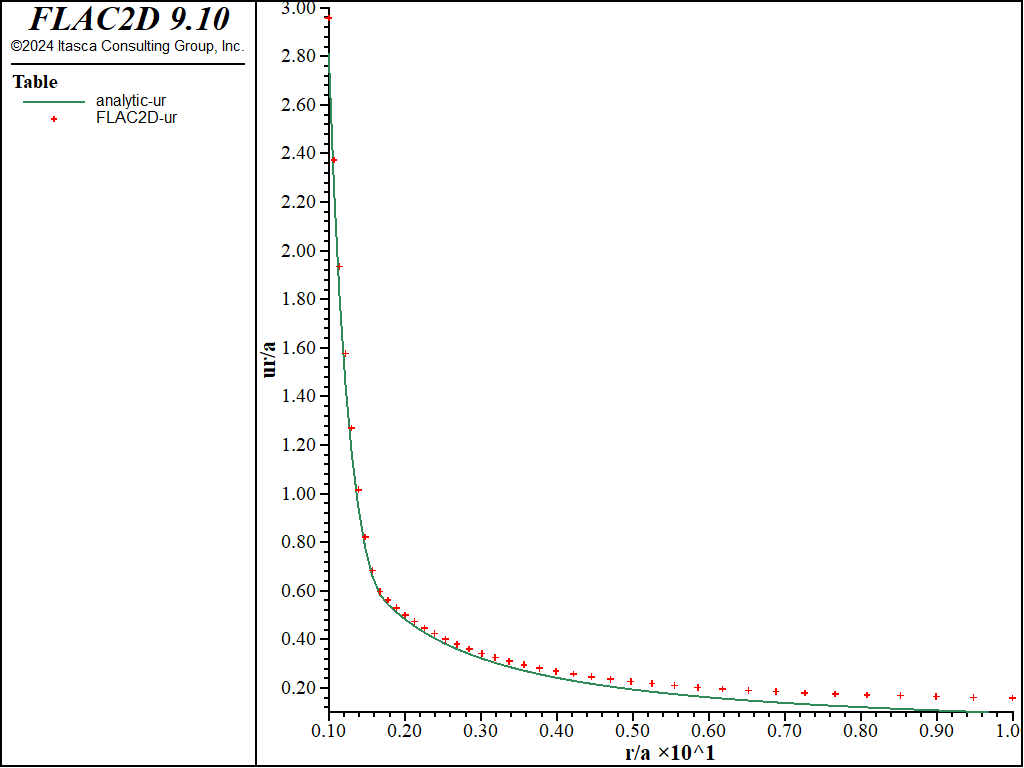
Figure 9: NMD radial displacement solution comparison—associated (analytical values = lines; numerical values = crosses).
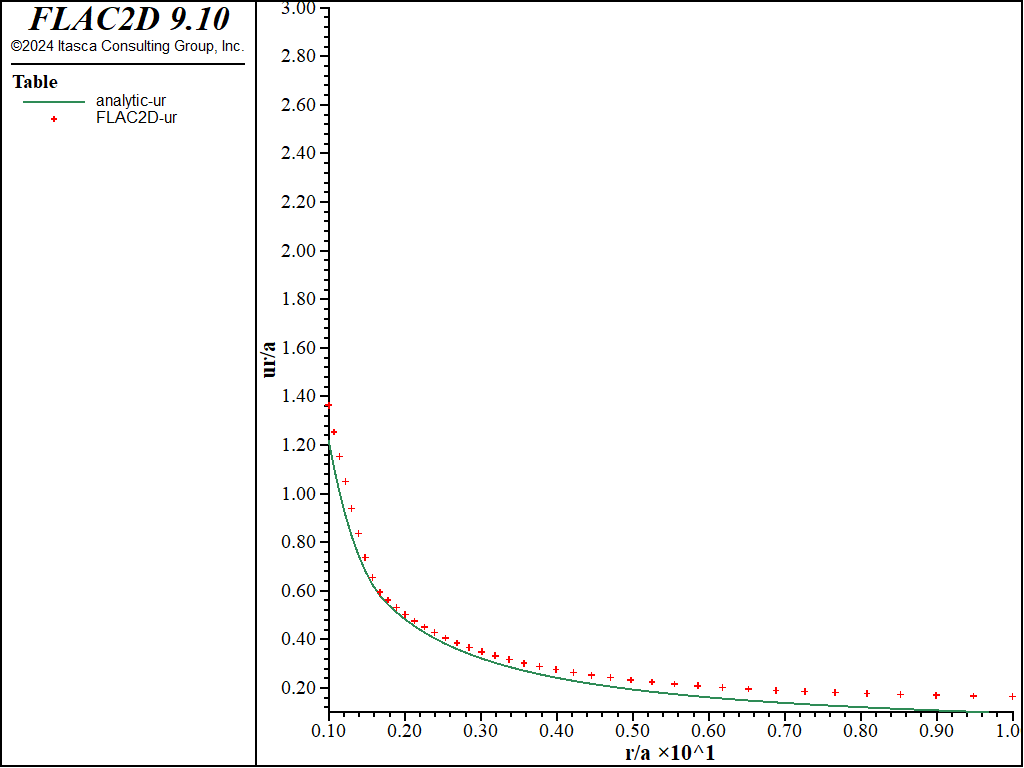
Figure 10: NMD radial displacement solution comparison—nonassociated (analytical values = lines; numerical values = crosses).
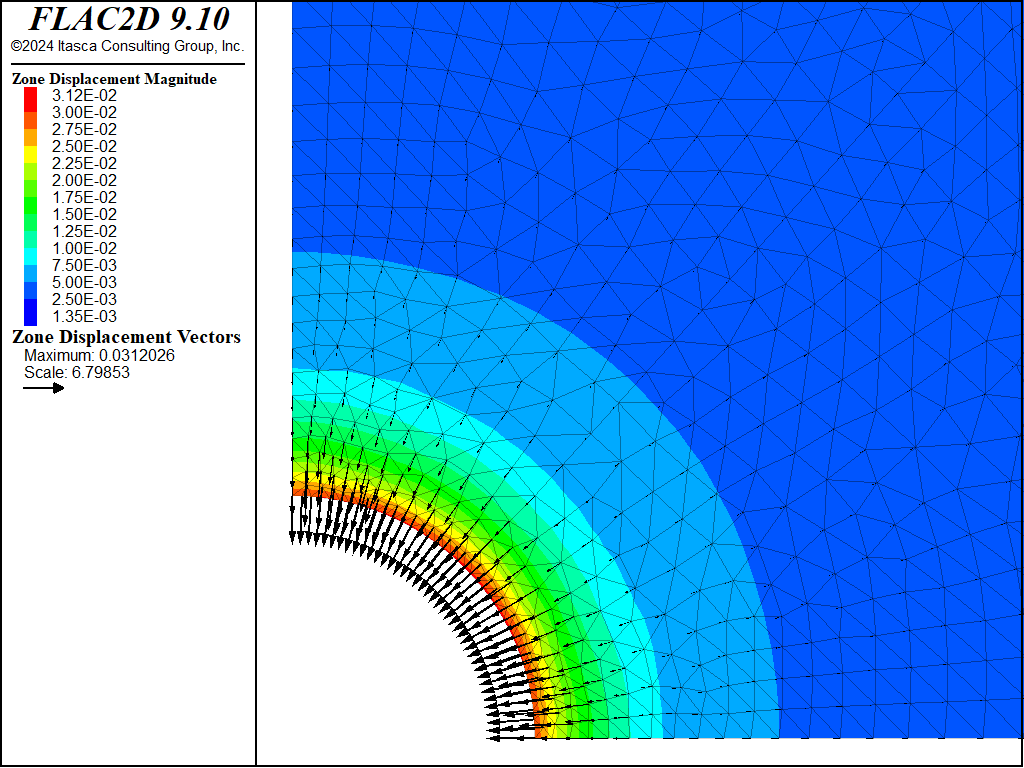
Figure 11: NMD FLAC2D displacement contours and displacement vectors—associated.
Reference
Salençon, J. “Contraction Quasi-Statique D’une Cavite a Symetrie Spherique Ou Cylindrique Dans Un Milieu Elastoplastique,” Annales Des Ponts Et Chaussees, 4, 231-236 (1969).
Data File
associated.dat
;---------------------------------------------------------------------
; numerical solution for a long tunnel in pre-stressed
; Mohr Coulomb material (salencon problem)
; associated and non-associated plastic flow
;---------------------------------------------------------------------
model new
model large-strain off
; Create zones
zone create2d sector-quad size 1 30 30 ratio 1 1 1.1 ...
point 1 10 0 point 2 0 10 dimension 1 1
; Assign constitutive model and properties
zone cmodel assign mohr-coulomb
zone property bulk 3.9e9 shear 2.8e9 cohesion 3.45e6
zone property friction 30. dilation 30. tension 1.e10 ; associated flow
; Initialize stress
zone initialize stress xx -30e6 yy -30e6 zz -30e6
; Apply boundary conditions
zone face apply velocity-normal 0.0 range union position-x 0 position-y 0
zone face apply stress-normal -30e6 range union position-x 10 position-y 10
; Take some histories
zone history displacement-x position 1 0
zone history velocity-x position 1 0
zone history unbalanced-force-y position 1 0
history interval 20
; Solve
model solve ratio-local 1e-4
; Save the model
model save 'associated'
Endnote
⇐ Cylindrical Hole in an Infinite Hoek-Brown Medium (FLAC2D) | Rough Strip Footing on a Cohesive Frictionless Material (FLAC2D) ⇒
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Aug 13, 2024 |
