Smooth Circular Footing on an Associated Mohr-Coulomb Material
Problem Statement
Note
To view this project in FLAC3D, use the menu command . Choose “VerificationProblems/CircularFooting” and select “CircularFooting.f3prj” to load. The main data file used is shown at the end of this example. The remaining data files can be found in the project.
The bearing capacity of a smooth circular footing on a Mohr-Coulomb medium is determined numerically in this section. The footing, represented by a circle of radius \(a\), is located on an associated material with the following properties:
| shear modulus (\(G\)) | 0.1 GPa |
| bulk modulus (\(K\)) | 0.2 GPa |
| cohesion (\(c\)) | 0.1 MPa |
| friction angle (\(\phi\)) | 20° |
| dilation angle (\(\psi\)) | 20° |
Semi-Analytical Solution
Cox et al. (1961) have numerically solved the slip-line equations for this axisymmetric-footing problem. The semi-analytical value of the average pressure over the footing at failure for a friction angle of 20° is found to be
in which q is the bearing capacity and c is the cohesion of the material. The corresponding slip-line net, as referenced in Chen (1975), is sketched in Figure 1.
Figure 1: Cox slip-line net for a smooth circular footing \(\phi\) = 20°.
FLAC3D Model
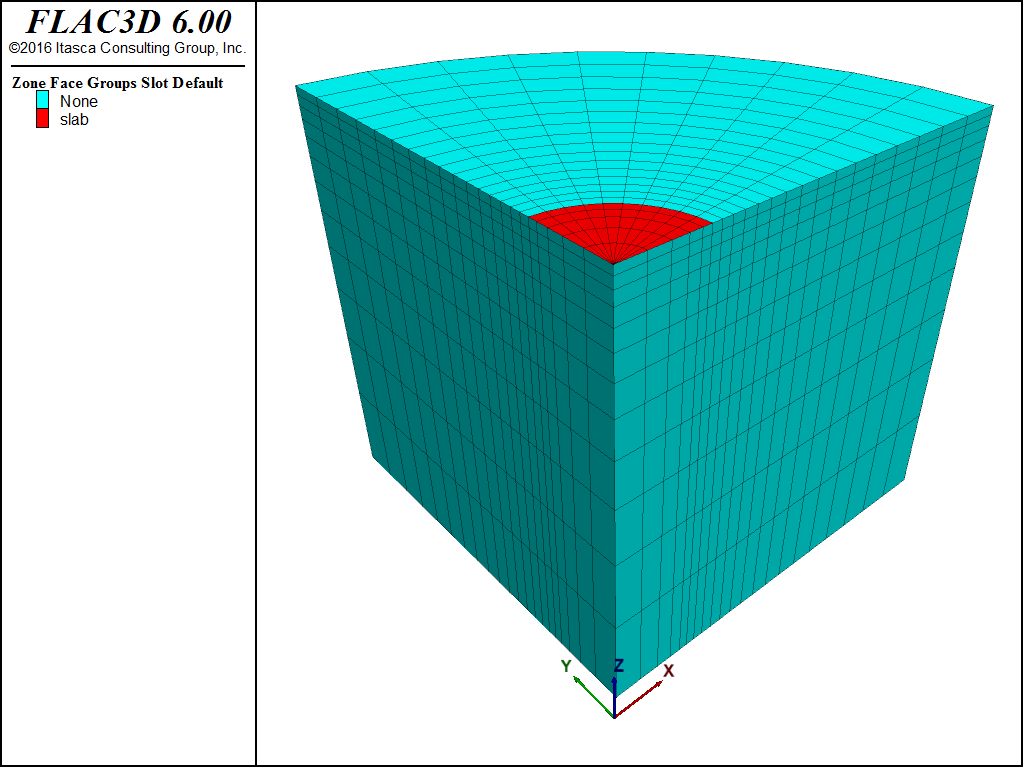
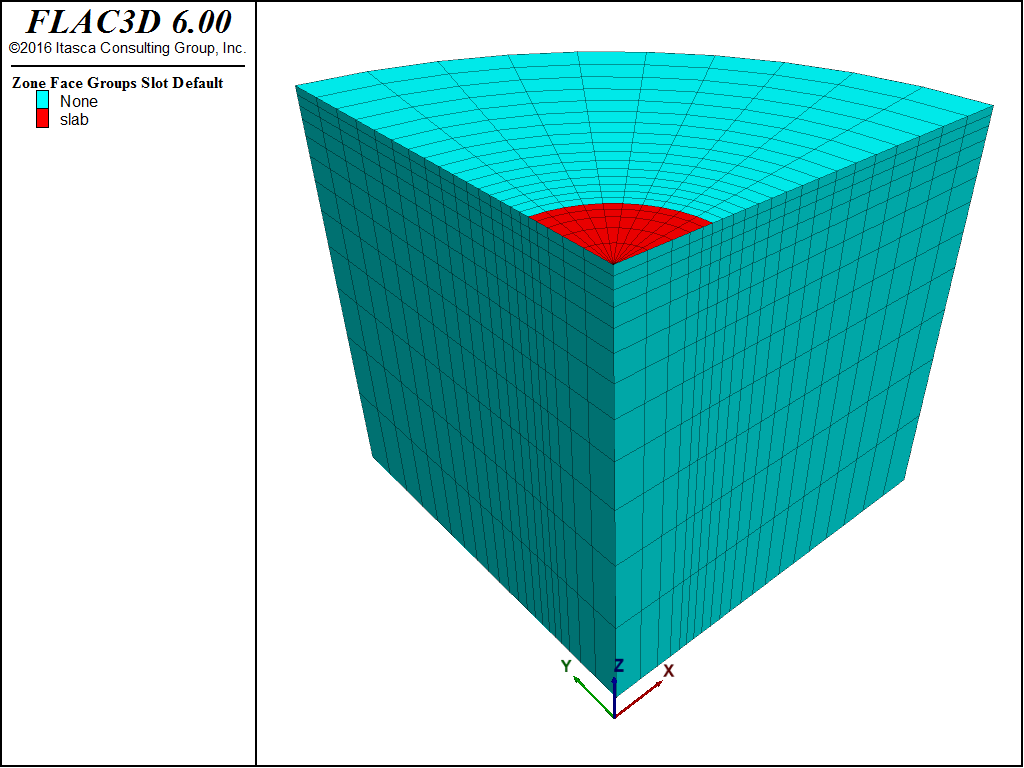
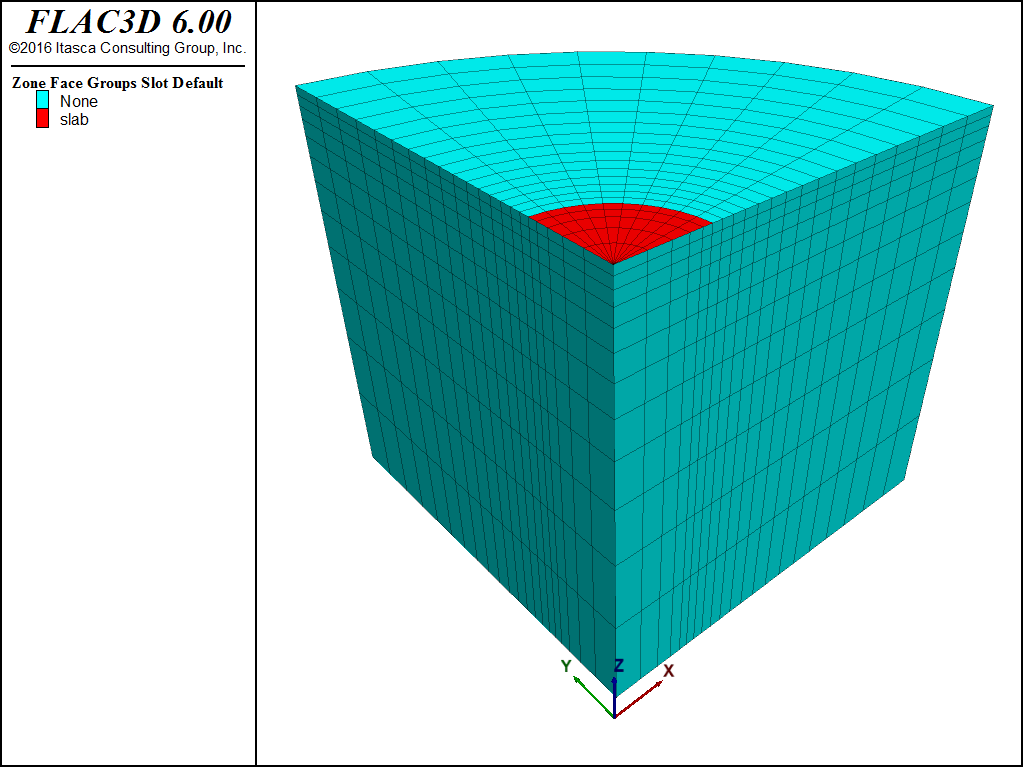
Quarter symmetry is taken into consideration for this problem as a means to illustrate the three-dimensional modeling capabilities of FLAC3D. The domain used for the numerical simulation is the quarter cylinder sketched in Figure 2. A system of coordinate axes is selected with the x- and y-axes in the plane of the cylinder upper-base, and the z-axis pointing upward along the cylinder axis. The slab is represented by a disk segment with radius a. The radius of the domain is 15 m, and its height is 10 m.
Figure 2: Domain for FLAC3D simulation—quarter symmetry.
The boundary conditions applied to this domain are sketched in Figure 3. The displacement of the symmetry boundaries at x = 0 and y = 0 is restricted in the x- and y-directions, respectively. The displacement of the circular boundary, and that of the cylinder base, is restricted in all directions. A downward velocity is applied to the gridpoints representing the extent of the footing in the negative z-direction.
Figure 3: Boundary conditions for FLAC3D analysis—quarter symmetry.
The domain is discretized into a regular radial pattern of 2000 zones, as represented in Figure 4. The radius, a, representing the footing, extends four rings of zones in the radial direction, over which the velocity is applied, plus half the distance to the gridpoints adjacent to the last gridpoints with applied velocity. The footing radius that corresponds to the gridpoints with applied velocity is then a = 3.165 m. A velocity of magnitude 2.0 × 10-5 m/step is applied at the footing nodes for a total of 9600 timesteps.
The FISH function load contained in file “footing-load.f3dat” computes the numerical value of the normalized average footing pressure, p/c.
Figure 4: FLAC3D grid.
Results and Discussion
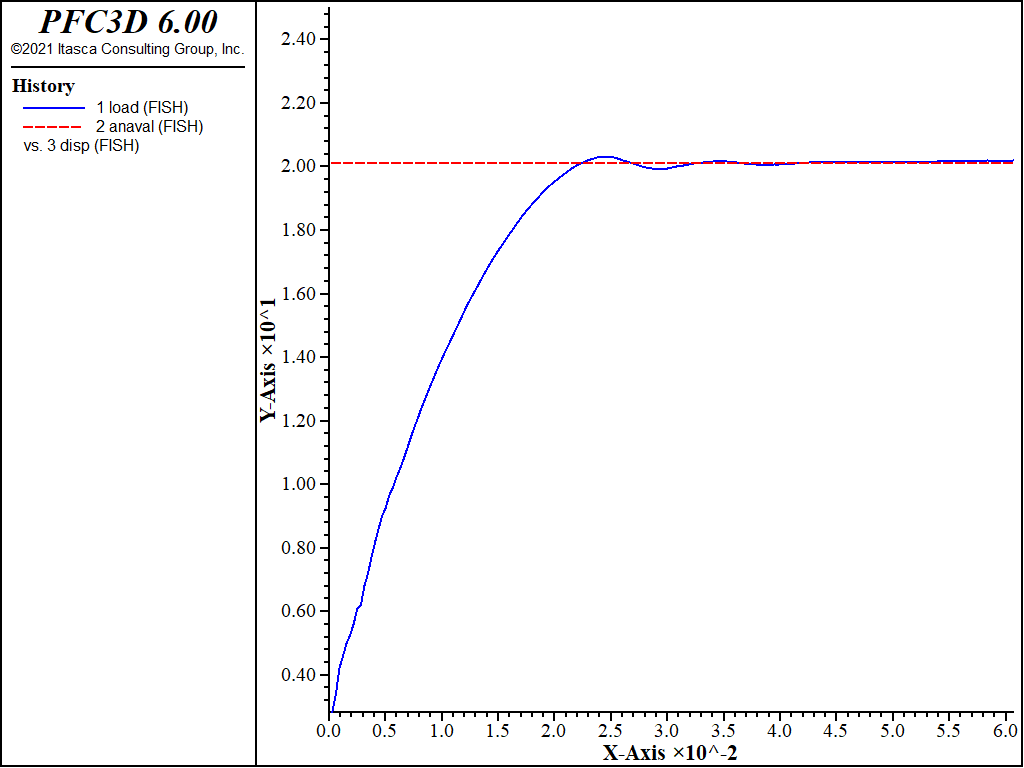
The load-displacement curve corresponding to the numerical simulation is presented in Figure 5, in which load is the normalized average footing pressure, p/c, anaval is the analytical value of the normalized bearing capacity, q/c, and disp is the normalized vertical displacement, u_z/a. The numerical value of the bearing capacity, q, is 2028 kPa, and the relative error is 0.4% when compared to the analytical value of 2010 kPa.
Figure 5: Load-displacement curve.
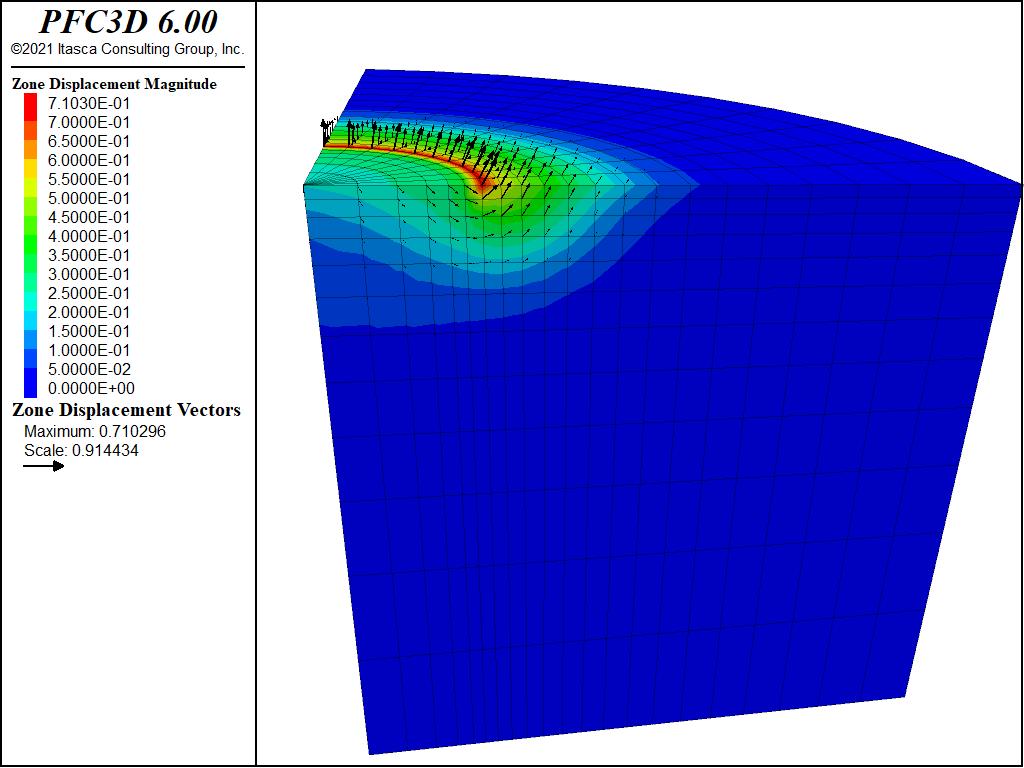
Velocity contours and velocity vectors at the end of the run on a radial plane are presented in Figure 6, showing good agreement with the mechanism in Figure 1.
Figure 6: Velocity field at collapse load.
References
Chen, W.-F. “Bearing Capacity of Square, Rectangular and Circular Footings,” in Limit Analysis and Soil Plasticity, Developments in Geotechnical Engineering 7, Ch. 7, pp. 295-340, New York: Elsevier Scientific Publishing Co. (1975).
Cox, A. D., G. Eason and H. G. Hopkins. “Axially Symmetric Plastic Deformation in Soils,” Phys. Trans. Royal Soc. London, Series A, 254(1036), 1-45 (1961).
Data File
;---------------------------------------------------------------------
; circular smooth slab on Mohr-Coulomb material (Cox problem)
; -associated plastic flow-
;---------------------------------------------------------------------
model new
model largestrain off
; Create zones
zone create cylindrical-shell point 0 (0,0,0) point 1 (0,15,0) ...
point 2 (0,0,15) point 3 (15,0,0) ...
point 4 (0,15,15) point 5 (15,0,15) ...
point 8 (0,3,0) point 9 (3,0,0) ...
point 10 (0,3,15) point 11 (3,0,15) ...
size 16 12 10 5 ratio 1.1 0.8 1 0.75 ...
fill group 'inner'
; Assign constitutive model and properties
zone cmodel assign mohr-coulomb
zone property bul 2.e8 shea 1.e8 cohesion 1.e5
zone property friction 20. dilation 20. tension 1.e10
; Name surfaces
zone face skin
zone face group 'slab' range group 'inner' group 'Top'
; Boundary Conditions
zone face apply velocity-normal -2e-5 range group 'slab'
zone face apply velocity-normal 0.0 range group 'South'
zone face apply velocity-normal 0.0 range group 'West'
zone face apply velocity (0,0,0) range group 'East' or 'North' or 'Bottom'
; Call FISH function that calculates footing load
call 'footing-load'
; Take some histories
history interval 50
fish history @load
fish history @anaval
fish history @disp
model history mechanical ratio-local
; Cycle till stable velocity field
model cycle 9600
; Save the model
model save 'cox'
list @load
list @anaval
list @err
⇐ Rough Strip Footing on a Cohesive Frictionless Material | Smooth Square Footing on a Cohesive Frictionless Material ⇒
| Was this helpful? ... | PFC 6.0 © 2019, Itasca | Updated: Nov 19, 2021 |